Który bliźniak jest starszy?
Wprowadzenie
Jeśli będziesz podążał za tym projektem, zostaniesz doprowadzony do zdumiewającego wniosku! Przypuśćmy, że jeden z pary identycznych bliźniaków wyrusza w podróż w kosmos, a następnie wraca, aby porównać swój (powiedzmy, że jej) wiek z wiekiem drugiego bliźniaka, który pozostał w tym samym miejscu na Ziemi. Okazuje się, że po podróży jedna z bliźniaczek będzie młodsza od swojej siostry! Zapewne pytasz, jak to możliwe, a celem tego projektu jest pokazanie Ci, jak to możliwe.
Zacznijmy od zgadywanki – na końcu dowiemy się, czy miałeś rację! Załóżmy, że podróżująca bliźniaczka wyrusza w 12-letnią podróż – 6 lat z domu i 6 lat z powrotem. Oczywiście po powrocie będzie o 12 lat starsza. To co musisz zrobić, to zgadnąć o ile lat będzie starszy bliźniak, który nie podróżuje….! Muszę Ci powiedzieć, jak szybko porusza się poruszający się bliźniak – powiedzmy cztery piąte prędkości światła – choć śmiem twierdzić, że nie pomoże Ci to zbytnio w zgadywaniu! Pozwólcie, że zasugeruję, abyście zgadli liczbę całkowitą pomiędzy 1 a 30!
Zanim zajmiemy się bliźniakami, musimy przygotować pewne narzędzia, które będą nam potrzebne, aby zrozumieć, co się dzieje. Będziemy często korzystać z pewnego rodzaju wykresu, zwanego wykresem czasoprzestrzennym. Nie martw się, jeśli nigdy wcześniej nie korzystałeś z grafów – postaramy się zacząć od podstaw.
?
Grafy
Najprostszy rodzaj grafu to po prostu obraz tego, co dzieje się na wybranej płaskiej powierzchni. Załóżmy, że siedzimy przy stole lub biurku, mamy dwie linijki i dużą kartkę papieru. Zaczynając od lewego dolnego rogu, połóż jedną linijkę na dole i jedną na górze po lewej stronie, a pomiędzy nimi kartkę papieru. To, co masz, powinno wyglądać tak:
Punkt, w którym spotykają się dwie linijki (zero na obu skalach), nazwiemy początkiem, lub w skrócie O, a linijki zapewnią dwie osie . Zgodnie z konwencją, oś wzdłuż dołu będziemy nazywać osią x, a oś w górę boku osią y. Każdy punkt na papierze możemy oznaczyć wartościami $x$ i $y$. Na przykład, początek ma wartości $x=0$, $y=0$. Punkt $1cm$ od osi y i $2cm$ od osi x ma wartości $x=1$, $y=2$ (naprawdę mam je na odwrót!).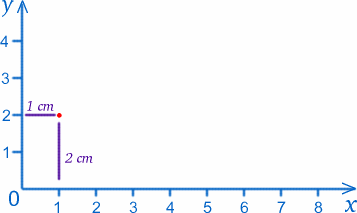
Ćwiczenie Narysuj swój własny wykres i zaznacz na nim następujące punkty:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Jaki kształt tworzą?
Wyobraź sobie teraz kilka mrówek o bardzo brudnych stopach. Przypuśćmy, że jedna z nich chodzi po papierze zachowując zawsze odległość $1cm$ od osi x. Jej droga byłaby linią, opisaną równaniem $y=1$ (wymyślny sposób powiedzenia tego, co zostało powiedziane słowami w poprzednim zdaniu). Inna mrówka może chodzić zawsze 3cm$ od osi y, a jej ścieżka miałaby równanie $x=3$. Bardziej oryginalna mrówka może chodzić tak, że jej odległość od obu osi jest zawsze taka sama; przechodziłaby przez $x=1$, $y=1$; $x=2$, $y=2$; itd, a jej droga byłaby określona równaniem $x=y$.
Wykresy czasoprzestrzenne
W tym rozdziale narysujemy kilka wykresów, które wyglądają bardzo podobnie do tych z poprzedniego rozdziału, ale ich znaczenie będzie zupełnie inne. Nadal mamy dwie osie, a ta oznaczona jako $x$ nadal reprezentuje odległość w pewnym kierunku. Jednak ta, która była oznaczona jako $y$ jest teraz oznaczona jako $t$, która reprezentuje czas, mierzony powiedzmy w sekundach.Wyobraźmy sobie na przykład piłkę w stałym punkcie $3cm$ od O; jej ścieżką w czasoprzestrzeni będzie linia prosta $x=3$. Załóżmy teraz, że piłka toczy się po prostej; wtedy punkty na wykresie odpowiadałyby położeniom piłki w poszczególnych chwilach np. $x=5$, $t=4$ odpowiadałyby temu, że piłka znajduje się $5cm$ od początku $4$ sekundy po rozpoczęciu pomiaru czasu.
Ćwiczenie Wykreśl na wykresie punkty odpowiadające następującym zdarzeniom w historii piłki: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Jak byś to zinterpretował?
Teraz spróbuj $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Co zauważyłeś w tych punktach? 
Jeśli tor kulki jest na wykresie linią prostą, to znaczy, że kulka porusza się ze stałą prędkością (być może z prędkością zerową). W takim przypadku możemy obliczyć prędkość widząc, jaką odległość pokonuje piłka w ciągu jednej sekundy – dzielimy zmianę wartości x przez odpowiadającą jej zmianę wartości t. Tak więc w naszym drugim przykładzie prędkość piłki wynosi $2cm/sek$. Czy się zgadzasz?
Ćwiczenie Narysuj wykres przedstawiający ruch kulki, która porusza się do tyłu i do przodu między dwoma punktami, ze stałą prędkością (ale oczywiście okresowo zmienia kierunek).
Zrobimy teraz z naszym wykresem coś dość dziwnego. W teorii zwanej szczególną względnością , która jest tym, co sprawia, że interesujące jest myślenie o bliźniakach i podróżach kosmicznych, często musimy wykreślać promienie świetlne na naszych wykresach. Promienie świetlne poruszają się w pustej przestrzeni ze stałą i bardzo dużą (ale skończoną) prędkością; promień światła docierający do nas ze Słońca wyszedł stamtąd około $8$ minut temu. (Kiedyś wierzono, że światło porusza się nieskończenie szybko, tak że można zobaczyć gwiazdy w momencie ich obserwacji, ale obecnie wiadomo, że to nieprawda). Mówiąc dokładniej, prędkość światła wynosi około 3000000000000cm/sek$! Mogłoby to prowadzić do bardzo dziwnych skal na osiach wykresu czasoprzestrzennego, więc zdecydujemy się mierzyć odległość w inny sposób; jednostkami na osi x będą fotosekundy, czyli odległość pokonywana przez światło w ciągu jednej sekundy. (Jeśli skalą dla $t$ są lata, odpowiadającą im skalą x będą lata świetlne). 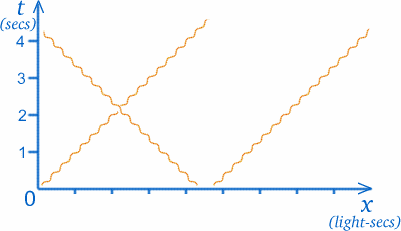
Dużą zaletą tego jest to, że ścieżka promienia świetlnego będzie zawsze pod kątem $45$ stopni do osi. Oznacza to, że promień światła przez O będzie pod równymi kątami do obu osi, jak widać na rysunku. (Chociaż światło porusza się ze stałą prędkością, więc jego droga jest linią prostą, przedstawiamy ją za pomocą linii falistej, jak pokazano na rysunku, aby odróżnić promienie świetlne od dróg innych obiektów o masie.)
?
Pomiar czasu
Mamy zwyczaj zakładać, że gdy ludzie nie zgadzają się co do tego, która jest godzina, czyjś zegarek się myli, a może ludzie są w różnych strefach czasowych! Ale to jest nawet bardziej skomplikowane niż to! Zgodnie ze szczególną względnością, dwie osoby mogą znajdować się w tym samym miejscu i korelować swoje zegarki, ale jeśli jedna z nich porusza się względem drugiej, to w konsekwencji nie będą się zgadzać co do tego, która jest godzina. Niestety, jeśli połączysz siły z przyjacielem i spróbujesz przetestować tę teorię, będziesz rozczarowany, nie dlatego, że teoria jest błędna, ale dlatego, że przy prędkości, z jaką prawdopodobnie będziesz w stanie biegać, nawet jeśli jesteś super-sportowcem, efekt będzie zbyt mały, aby go zaobserwować. Dopiero gdy prędkości stają się bardzo duże (znaczne ułamki prędkości światła), można zaobserwować to dziwne zjawisko, a i wtedy tylko przy użyciu niezwykle dokładnych zegarów.
Aby zobaczyć, jak to może działać, rozważmy „eksperyment myślowy” podobny do tego, który zasugerował Einstein. (Jest to raczej eksperyment „myślowy” niż rzeczywisty, ponieważ nie da się go w rzeczywistości przeprowadzić, z czego zdajesz sobie sprawę). Załóżmy, że obserwujesz zegar na Big Benie przez bardzo silny teleskop, oddalając się od niego bardzo szybkim pociągiem, który minął zegar dokładnie w południe (wiem, że pociągi nie przejeżdżają tuż obok Big Bena, ale udawajmy!). Gdyby pociąg mógł poruszać się z prędkością światła, co by się stało ze wskazówkami zegara? Wyglądałoby na to, że stoją w miejscu, obie wskazują $12$! Dlaczego? Dzieje się tak dlatego, że światło emitowane przez wskazówki (lub odbite od nich) w południe oddalałoby się od zegara z dokładnie taką samą prędkością, z jaką porusza się pociąg, a światło emitowane później nie mogłoby dogonić pociągu! Weird!
Can you see why this is a „thought experiment” (quite apart from the fact that trains don’t go past Big Ben)? To dlatego, że pociąg nie mógłby w rzeczywistości poruszać się z prędkością światła (o czym mówi nam szczególna względność – jakikolwiek obiekt, który cokolwiek waży, nigdy nie może poruszać się tak szybko jak światło). Ale przypuśćmy, że pociąg poruszałby się z połową prędkości światła (wciąż bardzo szybko) – zobaczylibyśmy, że wskazówki zegara poruszają się, ale wolniej niż te na naszym zegarku! Pomiar czasu zależy od tego, jak się poruszasz!
Jak to możliwe? Aby to zrozumieć, rozważmy specjalny rodzaj zegara, zegar świetlny. Raczej nie znajdziesz takiego obok swojego łóżka, budzącego cię rano. Składa się on ze źródła światła emitującego sygnały, które pokonują odległość D, a następnie są odbijane z powrotem do źródła. Przerwa czasowa lub interwał pomiędzy każdym wysłaniem sygnału a jego odebraniem określa tyknięcia zegara; występują one w odstępie $2T$, gdzie \begin{equation} {T} = {D/c} \end{equation}, gdzie $c$ oznacza prędkość światła. (Pamiętaj, że prędkość = odległość/czas, więc czas = odległość/prędkość.)
Załóżmy teraz, że poruszająca się rakieta przenosi taki zegar – doświadczenie załogi będzie takie, że tyknięcia występują w odstępach $2T$. Przypuśćmy teraz, że załoga nieruchomej rakiety obserwuje zegar poruszającej się rakiety i porównuje go ze swoim własnym, również tykającym w odstępach czasu $2T$. Co zobaczą? Poniższe diagramy powinny podpowiedzieć odpowiedź. (Przepraszam, że moje rakiety wyglądają bardziej jak ryby!) 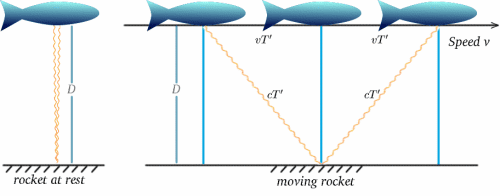
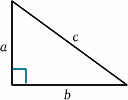
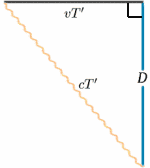
W przypadku poruszającej się rakiety, światło odbija się od lustra w połowie drogi między wysłaniem sygnału a jego odbiciem. Od nieruchomej rakiety, czas podróży wydaje się być $2T^{ prime}$ powiedzmy. Możemy to obliczyć korzystając z bardzo ważnego twierdzenia (wymyślna nazwa dla czegoś, co zostało udowodnione jako prawdziwe w matematyce!) – twierdzenia Pitagorasa.
 |
 |
Ale nie wyciągaj pochopnych wniosków – rzeczy nie zawsze są tym, czym się wydają…! Droga podróżującej bliźniaczki wygląda na dłuższą, ale czy to oznacza, że doświadczyła ona więcej czasu? Aby zobaczyć, jak podchwytliwe jest tego typu pytanie, pomyśl o sytuacji, która może być dość podobna. Załóżmy, że mieszkasz w Trumpington, po południowej stronie Cambridge, i chcesz zrobić zakupy w Tesco na północnym krańcu centrum miasta (tak blisko jak możesz, unikając stref dla pieszych), na obwodnicy lub na by-passie – patrz diagram poniżej. 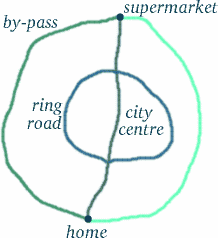
W większości pór dnia okazuje się, że najdłuższa trasa – obwodnica – zajmuje najmniej czasu, a następnie obwodnica. Czy teraz jesteś przekonany, że oczywista odpowiedź nie zawsze jest właściwa??
Widzieliśmy, jak czas jest mierzony za pomocą sygnałów świetlnych. Gdy mamy już dokładny zegar, możemy następnie zmierzyć odległość za pomocą sygnałów świetlnych lub radarowych odbitych od odległego obiektu; odległość będzie równa połowie czasu podróży światła, pomnożonego przez prędkość światła.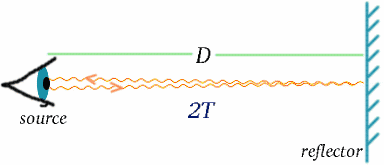
Begin{equation} {D} = {cT}quad (7) \(7) \end{equation} Podobnie jak czas, odległość jest wielkością, w której wynik pomiaru zależy od tego, jak porusza się obserwator.
Współczynniki K
Opiszę teraz ideę, która powinna nam pomóc w wykonywaniu obliczeń tego typu efektów, o których mówiłem.
Załóżmy, że astronauta B (dla Bena) znajduje się w rakiecie poruszającej się z prędkością $c/5$ od innego astronauty A (dla Alf) na stacji kosmicznej. Raz w roku, 13 marca, Alf przesyła Benowi życzenia urodzinowe. Załóżmy, że wiadomość radiowa zawierająca te życzenia w roku 2010 jest mierzona przez stację kosmiczną na odległość pół roku świetlnego, aby dotrzeć do rakiety, co zajmuje pół roku. Następna wiadomość jest wysyłana dokładnie rok później. Kiedy ten sygnał radiowy przebył pół roku do miejsca, w którym astronauta Ben odebrał poprzedni sygnał, rakieta przesunęła się o jedną piątą roku świetlnego dalej, więc ten sygnał musi przebyć dłuższą drogę, aby dogonić rakietę; w rzeczywistości czas zmierzony przez Alfa, kiedy sygnał dotarł do rakiety, to trzy czwarte roku po tym, jak został wysłany – patrz diagram poniżej. Biedny Alf dochodzi do wniosku, że wysyłane co roku życzenia urodzinowe będą odbierane przez Bena w odstępach jednego i ćwierć roku, zgodnie z zegarem Alfa. 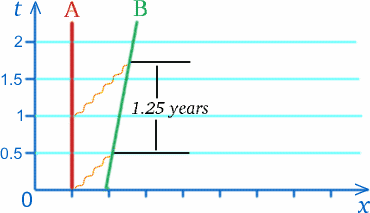
To nie mówi nam, co Ben będzie mierzył w tych odstępach czasu, ale sugeruje, że może to nie być rok! Podobny efekt wystąpi dla sygnałów wysyłanych od Bena do Alfa.
Przyjrzyjrzyjmy się teraz ogólnemu przypadkowi i uściślijmy to. Rozważmy dwóch obserwatorów Alf i Ben oddalających się od siebie ze stałymi prędkościami. 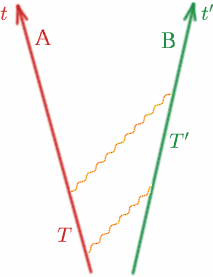
Alf wysyła sygnał świetlny, a następnie kolejny w czasie $T$ później. Ben odbiera te dwa sygnały w odstępie czasu $T^{prime}$, zgodnie ze swoim zegarem. Następnie definiujemy wielkość $K$ przez \begin{equation} {K} = {T^{prime}/T}. \quad (8) \end{equation} Zauważmy, że gdyby Alf i Ben poruszali się z tą samą prędkością (w tym samym kierunku!), to $K$ byłoby równe jeden. Zobaczymy dokładniej, jak $K$ zależy od względnej prędkości Alf’a i Ben’a. $K$ jest czasami nazywany współczynnikiem przesunięcia Dopplera, a efekt jest podobny do tego dla fal dźwiękowych – pewnie wszyscy znacie zmianę dźwięku syreny karetki lub samochodu policyjnego, gdy zbliża się, a następnie oddala.
Jak możemy zmierzyć $K$? Oczywistym sposobem jest dla obserwatorów do prowadzenia rejestrów, kiedy sygnały świetlne są wysyłane i odbierane tak, że mogą one wypracować $T$ i $T^{prime}$, a więc $K$, kiedy spotykają się później. Inną możliwością byłoby, aby jeden z nich miał bardzo potężny teleskop, za pomocą którego mógłby obserwować zegar drugiego (to jest naprawdę pociąg przejeżdżający obok Big Bena wszystko od nowa!).
Musimy przyjąć pewne założenia dotyczące tej liczby $K$, aby była ona dla nas użyteczna. Zakładamy najpierw, że gdy Alf i Ben poruszają się ze stałymi prędkościami, to $K$ nie zależy od tego, kiedy $T$ i $T^{prime}$ są mierzone, ani nie zależy od tego, jak duże jest $T$. Więc na przykład, jeśli Alf będzie czekał dwa razy dłużej między wysyłaniem sygnałów świetlnych, $K$ będzie takie samo. Sprawdź, czy potrafisz uzupełnić liczby $T_1^{pierwiastek}$, $T_2^{pierwiastek}$, $T_3^{pierwiastek}$ w tym przypadku.
?
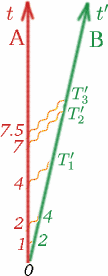
(Zauważ, że dobrze jest zacząć mierzyć czas, gdy dwaj obserwatorzy są razem i obaj mogą w tym momencie ustawić swoje stopery na zero). Tak więc w ogólności mamy
?
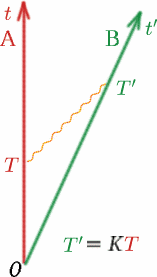
Drugą rzeczą, którą zakładamy, a która jest równie ważna, jest to, że $K$ mierzone przez Bena dla sygnałów świetlnych od Alfa jest takie samo, jak mierzone przez Alfa dla sygnałów świetlnych od Bena. Dlaczego tak zakładamy? Wyobraźmy sobie dwa identyczne samochody stojące tyłem do siebie na drodze. Samochód $A$ stoi w miejscu, a samochód $B$ rusza z prędkością $50km/h$ z dala od samochodu $A$. Pasażerowie patrzący przez tylną szybę $A$ zobaczą $B$ znikający w odpowiednim tempie. Pasażerowie w $B$ zobaczą bardzo podobny obraz, jeśli spojrzą przez tylne okno – samochód $A$ będzie wydawał się oddalać z taką samą prędkością! Czy kiedykolwiek miałeś to niesamowite doświadczenie siedzenia w pociągu i myślenia, że właśnie ruszył, kiedy okazuje się, że to sąsiedni pociąg ruszył w przeciwnym kierunku, a Twój pociąg jest nadal stacjonarny? To założenie umożliwia jednemu obserwatorowi pomiar $K$ przez radar bez współpracy z drugim. Czy ktoś może zgadnąć jak? Pozwólcie, że wam podpowiem.
Załóżmy jak zwykle, że Alf i Ben oddalają się od siebie ze stałą prędkością. Alf wysyła dwa sygnały w odstępie $T$, Ben odbija je w odstępie $T^{prime}$, a Alf odbiera je z powrotem w odstępie $T^{prime}$. Jak Alf może obliczyć $K$?
?
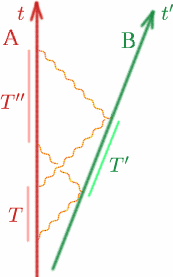
begin{equation} {T^{prime}} = {K T} \quad (9), \end{equation} \^begin{equation} {T^{prime}} = {K T^{prime}} ^quad (10) ^end{equation} Zatem \begin{equation} {T^{prime}} = {K(K T)} = {K^2 T} \quad (11) \end{equation} więc mamy \begin{equation} {K} = {{sqrt{T^{prime}/T}}. \quad (12) \end{equation} Problem W celu wykonania skomplikowanego manewru dokowania konieczne jest, aby dwa statki kosmiczne znajdowały się względem siebie w spoczynku. Opracuj prosty eksperyment sprawdzający, czy tak jest.
Zależność K od prędkości
Wiemy już, że jeśli prędkość względna Alf i Ben jest równa zero, to $K$ = $1$. Jaka jest jego wartość dla prędkości ogólnych? Istnieje sprytny sposób, aby to opracować, który wykorzystuje ideę, o której właśnie mówiliśmy, plus ideę jednoczesności. Co to oznacza? Wyjaśnię to za chwilę.
Początkowo wyobraźmy sobie naszych zwykłych dwóch obserwatorów podróżujących od siebie ze stałą prędkością $v$. Załóżmy, że gdy są razem, obaj ustawiają swoje zegary na $t = 0$. W czasie $T$ według swojego zegara Alf emituje sygnał radiowy; Ben odbija go z powrotem w czasie $T’$ według swojego zegara, a Alf odbiera go ponownie w czasie $T^{prime}$ według swojego zegara. Narysujmy obrazek jak zwykle.
?
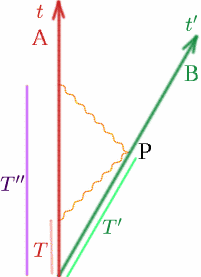
Teraz wiemy, że \u00{equation} {T^{prime}} = {K T}quad (13) \u00{equation} \^begin{equation} {T^{prime}} = {K T^{prime}} = {K^2 T}. \quad (14) \end{equation} Alf myśli więc, że czas podróży impulsu radiowego wynosi {T^{equation} {T^{prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{equation} i Alf oblicza, że odległość, $D$, między nim a Benem, jest połową odległości przebytej przez sygnał radiowy, czyli połowa prędkości razy czas: \{equation} {D} = {frac {1} {2} c(K^2-1)T}. \quad (16) \end{equation} Teraz wiemy, że odległość między Alfem a Benem ciągle się zmienia, więc musimy zapytać, kiedy (tzn. w jakim czasie) jest to odległość między Alfem a Benem. Tu właśnie potrzebujemy pojęcia równoczesności. Odległość jest wyraźnie mierzona, gdy Ben znajduje się w punkcie $P$, ale jakiemu czasowi odpowiada to dla Alfa? Cóż, Alf wie, że impuls radiowy pokonuje tę samą odległość na zewnątrz i z powrotem, więc zdarzenie $Q$, które Alf ocenia jako będące w tym samym czasie co $P$, będzie w połowie drogi między $T$ a $T^{pierwiastek}$. (Mówimy, że $Q$ jest jednoczesne z $P$ dla Alfa – oznacza to po prostu w tym samym czasie). Zatem czas w $Q$ to \begin{equation} {T_Q} = {frac {1} {2}(T+T”)} = {frac {1} {2} (K^2+1)T}. \quad (17) \end{equation} Alf wnioskuje więc, że Ben przebył odległość $D$ w czasie $T_Q$, więc jego prędkość $v$ jest dana wzorem \begin{equation} {v} = {frac {D} {T_Q}} = {frac {1} {2} c(K^2-1)T} { {frac {1}{2} (K^2+1)T}}. \quad (18) \end{equation} Mamy zatem \begin{equation} {{frac {v} {c}} = {{frac {K^2-1} {K^2+1}}. \quad (19) \end{equation} Możemy teraz rozpracować $K$ pod względem $frac {v} {c}$: \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c}})}, \quad (22) \end{equation} Dlatego {K^2} = {K^2(1- \frac{v}{c}}). {1- \frac{v}{c}}}}quad (23) \end{equation} a więc \begin{equation} {K} = \sqrt{{left({\frac{1+ \frac{v}{c}}{1- \frac{v}{c}}}}right)}}. \quad (24) \end{equation} Spróbuj wypracować kilka wartości K:
np. $v = c/4$ – to daje $K = \sqrt{5/3} = 1,291$.
Teraz spróbuj $v = c/2, 9c/10, 99c/100$.
Teraz nie ma znaczenia, czy Alf jest nieruchomy, a Ben się porusza, czy na odwrót – $K$ jest wciąż takie samo. Inaczej jest, gdy Alf i Ben zbliżają się do siebie, a nie oddalają – w takim przypadku przyjmujemy, że wartość $v$ jest ujemna, ale możemy skorzystać z tego samego wzoru.
np. jeśli Alf i Ben zbliżają się do siebie z prędkością względną $c/2$, to \begin{equation} K = \sqrt{{lewa({\frac{1+(-1/2)}{1-(-1/2)}}prawa)}} = \sqrt{{lewa({\frac{1/2}{3/2}}}prawa)}} = \sqrt{1/3}. \quad (25) \end{equation}. Obliczmy $K$ dla kilku typowych prędkości:
1) samolotów pasażerskich zbliżających się do siebie z prędkością 1000km/h$;
2) galaktyk w naszej gromadzie oddalających się od siebie z prędkościami względnymi 500km/s$;
3) samochodu zbliżającego się do policjanta z prędkością 100km/h$;
4) Ciebie idącego w kierunku przyjaciela z prędkością 5km/h$ Czy uważasz, że któryś z tych efektów byłby obserwowalny? Paradoks bliźniąt – nareszcie!
Co się dzieje? Dlaczego jest to paradoks? (Co w ogóle oznacza słowo paradoks?)
Rozważmy identyczne bliźniaczki, Albertynę i Brygidę! Albertina zostaje w domu w Londynie, podczas gdy Brigitta, ta żądna przygód, wyrusza w podróż kosmiczną. Oddala się ona od Ziemi na 6 lat, mierzonych jej zegarem, w bardzo szybkim statku kosmicznym, który porusza się z prędkością $v = 4c/5$. Następnie wraca z tą samą prędkością przez 6 lat. Zatem Brigitta mierzy czas 12 lat dla swojej podróży – jest o 12 lat starsza, gdy wraca do domu, do Albertyny w Londynie. Ale o ile lat starsza jest Albertina? Zobaczmy, czy Twoje przypuszczenie było słuszne, czy może tylko bliskie!
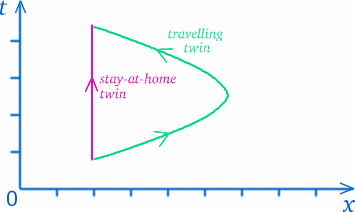
Narysujmy diagram czasoprzestrzenny: 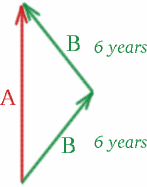
Podczas podróży Brigitty na zewnątrz bliźniaki oddalają się od siebie ze względną prędkością $v = 4c/5$, więc \begin{equation} {K^2} = {{frac{1+\frac{4}{5}}}{1-\frac{4}{5}}} = {9}, \quad (26) \end{equation} i mamy $K=3$. W drodze powrotnej Brigitta zbliża się do siebie z tą samą prędkością, więc \begin{equation} {K^2} = {\frac{1-\frac{4}{5}}}{1+\frac{4}{5}}} \quad (27) \end{equation} i mamy $K=1/3$. Aby obliczyć czas, który mierzy Albertina, musimy tylko umieścić jeden sygnał świetlny! Przypuśćmy, że Albertina wysyła sygnał w punkcie $S$, tak dobrany, że dociera on do Brigitty w punkcie $U$, w momencie, gdy ta zamierza zawrócić. 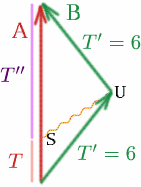
W takim razie ile wynosi $T$, jeśli $T^{prime}=6$ i $K=3$? Mamy ^begin{equation} {T^{prime}} = {K T} \quad (28) \end{equation}
więc $6=3T$ i $T=2$.
Spójrzmy teraz na to, co dzieje się w drodze powrotnej Brigitty. Ile wynosi $T^{prime}$? Mamy $T^{prime}=6$, $K=1/3$ i ^begin{equation} {T^{prime}} = {K T^{prime}}, ^quad (29) ^end{equation} więc $6=T^{prime}/3$ i $T^{prime}=18$. Zatem całkowity czas zmierzony przez Albertynę wynosi $T+T^{prime}=20$ lat, więc jest ona o 20 lat starsza, gdy się spotykają, podczas gdy Brigitta jest tylko o 12 lat starsza! Tak więc Albertina postarzała się o 8 lat więcej niż Brigitta!
Czy dobrze zgadłeś????
To, co możesz spróbować zrobić na własną rękę, to pewne eksperymenty z liczbami. Na przykład, możesz sobie wyobrazić, że Brigitta odbywa podróż trwającą, powiedzmy, 10+10=20$ lat i możesz obliczyć, jak szybko musi podróżować, aby Albertina postarzała się tylko o jeden rok więcej niż ona (tzn. na zegarze Albertiny minęło 21$ lat), kiedy Brigitta wróci. Może uda Ci się ustalić, czy możliwa byłaby realistyczna (tzn. osiągalna) podróż kosmiczna, w której bliźnięta starzałyby się inaczej o zauważalną ilość lat!
Teraz dlaczego to wszystko nazywa się paradoksem? Pamiętasz, co oznacza paradoks? Powiedzieliśmy wcześniej, że jeśli dwie osoby poruszają się ze stałą prędkością (a więc ze stałą prędkością względem siebie), to wiele z tego, co się dzieje, jest takie samo, niezależnie od tego, czy uznamy pierwszą z nich za nieruchomą, a drugą za poruszającą się, czy też na odwrót. Stosując ten argument do Albertyny i Brigitty, dlaczego nie możemy uznać, że Brigitta w swoim statku kosmicznym jest osobą, która siedzi nieruchomo, a Albertina na Ziemi odpływa, a następnie wraca. W ten sposób brzmi to dość głupio, ale mam nadzieję, że rozumiecie ideę. Wtedy spodziewalibyśmy się, że Brigitta będzie starsza od Albertyny, kiedy w końcu się spotkają. Ale powiedzieliśmy już, że Albertina jest wtedy starsza. Jak więc oba te stwierdzenia mogą być prawdziwe? To jest paradoks!
Czy widzisz, co jest nie tak??
Chodzi o to, że Brigitta nie porusza się ze stałą prędkością w stosunku do Albertyny w całej swojej podróży; ma dwa długie odcinki podróży, w których to robi, ale pomiędzy nimi jest prawdopodobnie krótki, ale bardzo ważny odcinek, w którym zwalnia, zatrzymuje się, a następnie przyspiesza w przeciwnym kierunku. To właśnie robi różnicę! Przyspieszenie jest prawdziwym fenomenem, jak zapewne wiesz z przejażdżek, które sprawiają, że czujesz się chory na jarmarku! Czy wiesz, jak można je wykryć za pomocą prostego urządzenia? 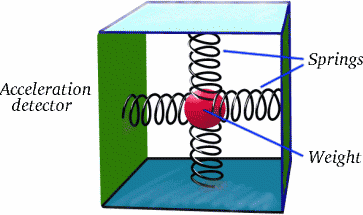
Co więc z tego wszystkiego wynika? Wydaje się to trochę niesprawiedliwe, że Brigitta może podróżować i zobaczyć więcej Wszechświata, ale kończy młodsza od swojej siostry bliźniaczki – życie nie zawsze wydaje się sprawiedliwe! Ale to powinno zachęcić Was do podróżowania – niekoniecznie w kosmos! – i bądźcie żądni przygód! Odnośniki Więcej dyskusji na temat paradoksu bliźniąt i opisanych tu technik można znaleźć w książce Flat and Curved Space-Times (Płaskie i zakrzywione czasy kosmiczne), autorstwa G.F.R. Ellisa i mojego (wydanej przez Oxford University Press w 1988 r.). Możesz również zajrzeć do książek Pana Tompkinsa, które w zabawny i przystępny sposób wprowadzają pojęcia szczególnej względności.
Możesz znaleźć recenzje książek Pana Tompkinsa i zamówić je na stronie Cambridge University Press, na przykład zobaczyć The New World of Mr Tompkins : George Gamow’s Classic Mr Tompkinsin Paperback
.