Introduktion

Om du följer detta projekt kommer du att få en fantastisk slutsats! Anta att en av ett par enäggstvillingar gör en resa i rymden och sedan återvänder för att jämföra sin (låt oss säga sin) ålder med åldern hos den andra tvillingen som har stannat kvar på samma plats på jorden. Det visar sig att den ena tvillingen kommer att vara yngre än sin syster efter resan! Du frågar dig säkert hur det kan vara möjligt, och syftet med det här projektet är att visa dig hur.
Låt oss börja med en gissningslek – vi får reda på om du har rätt i slutet! Anta att den resande tvillingen åker på en 12-årig resa – 6 år ut och 6 år tillbaka. Självklart kommer hon att vara 12 år äldre när hon kommer tillbaka. Vad du måste göra är att gissa hur mycket äldre den tvilling som inte reser kommer att vara….! Jag måste berätta för dig hur snabbt den rörliga tvillingen reser – låt oss säga fyra femtedelar av ljusets hastighet – även om jag vågar påstå att detta inte kommer att hjälpa dig särskilt mycket med din gissning! Låt mig föreslå att du gissar ett helt tal mellan 1 och 30!
Innan vi betraktar tvillingarna måste vi sätta upp vissa verktyg som vi kommer att behöva för att förstå vad som händer. Vi kommer att använda oss mycket av en viss typ av diagram som kallas rymdtidsdiagram. Oroa dig inte om du aldrig har använt grafer tidigare – vi ska försöka börja med grunderna.
?

Grafer

Den enklaste typen av grafer är bara en bild av vad som händer på en utvald plan yta. Låt oss anta att du sitter vid ett bord eller ett skrivbord och att du har två linjaler och ett stort papper. Börja i det nedre vänstra hörnet och placera en linjal längs botten och en uppåt på vänster sida, med pappret på plats mellan dem. Det du har ska se ut så här:

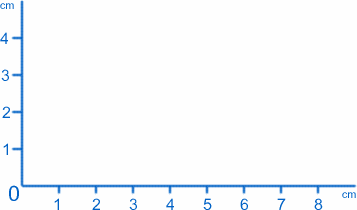
Vi ska kalla den punkt där de två linjalen möts (nollpunkten på båda skalorna) för ursprunget, eller O förkortat, och linjalen ger de två axlarna . Enligt konventionen ska vi kalla den längs botten för x-axeln och den längs sidan för y-axeln. Vi kan märka vilken punkt som helst på pappret med värdena $x$ och $y$, till exempel har ursprunget $x=0$, $y=0$. Punkten 1 cm$ från y-axeln och 2 cm$ från x-axeln har $x=1$, $y=2$ (jag har verkligen fått dem rätt!).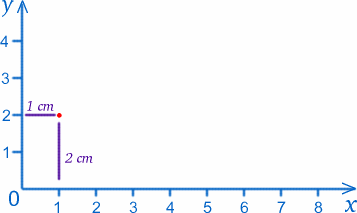

Övning Rita din egen graf och markera följande punkter:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Vilken form har de?
Föreställ dig nu några myror med mycket smutsiga fötter. Anta att en av dem går över pappret och alltid håller sig på ett avstånd av 1 cm$ från x-axeln. Dess väg skulle vara en linje som beskrivs av ekvationen $y=1$ (ett fint sätt att säga det som sägs med ord i föregående mening). En annan kanske går alltid 3 cm$ från y-axeln; ekvationen för dess bana skulle vara $x=3$. En något mer originell myra skulle kunna gå så att dess avstånd från båda axlarna alltid är detsamma; den skulle gå genom $x=1$, $y=1$; $x=2$, $y=2$; osv. och dess bana skulle ges av ekvationen $x=y$.

Rymd- och tidsdiagram

I det här avsnittet ska vi rita upp några grafer som ser mycket likartade ut som de i det föregående avsnittet, men deras innebörd kommer att vara ganska annorlunda. Vi har fortfarande två axlar, och den som är märkt $x$ representerar fortfarande avståndet i en viss riktning. Men den som var märkt $y$ är nu märkt $t$, som representerar tid, mätt i sekunder till exempel.Föreställ dig till exempel en boll vid en fast punkt 3cm$ från O; dess väg i rymdtiden kommer att vara den raka linjen $x=3$. Anta nu att bollen rullar längs en rak bana; då skulle punkter på grafen motsvara bollens positioner vid särskilda tidpunkter t.ex. $x=5$, $t=4$ skulle motsvara att bollen befinner sig $5cm$ från origo $4$ sekunder efter att tidsmätningen påbörjades.
Övningsuppgift Plotta punkter på grafen som motsvarar följande händelser i bollens historia: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Hur skulle du tolka detta?
Prova nu $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Vad lägger du märke till med dessa punkter?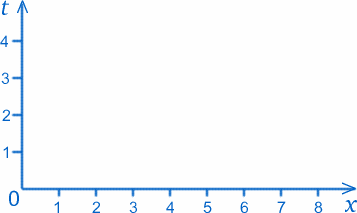
Om bollens bana är en rät linje på grafen betyder det att bollen rör sig med konstant hastighet (kanske hastighet noll). I det fallet kan vi räkna ut hastigheten genom att se hur långt bollen färdas på en sekund – vi delar förändringen i x-värdet med motsvarande förändring i t-värdet. Så i vårt andra exempel är bollens hastighet 2 cm/sek$. Håller du med?
Övningsuppgift Rita en graf som representerar rörelsen hos en boll som rör sig fram och tillbaka mellan två punkter, med konstant hastighet (men som regelbundet ändrar riktning, förstås).
Vi ska nu göra något ganska märkligt med vår graf. I den teori som kallas speciell relativitetsteori , som är det som gör det intressant att tänka på tvillingar och rymdresor, behöver vi ofta plotta ljusstrålar på våra grafer. Ljusstrålar färdas i det tomma rummet med en konstant och mycket stor (men ändlig) hastighet; en ljusstråle som når dig från solen lämnade den för ungefär $8$ minuter sedan. (Folk brukade tro att ljuset färdas oändligt snabbt så att man kunde se stjärnorna i samma ögonblick som man observerade dem, men det vet man nu att det är fel). För att vara mer exakt är ljusets hastighet ungefär $30000000000cm/sek$! Detta skulle kunna leda till mycket märkliga skalor på axlarna i ett rum-tidsdiagram, så vi väljer att mäta avståndet på ett annat sätt; enheterna på x-axeln kommer att vara ljussekunder, det vill säga den sträcka som ljuset färdas på en sekund. (Om skalan för $t$ är år kommer motsvarande x-skala att vara ljusår).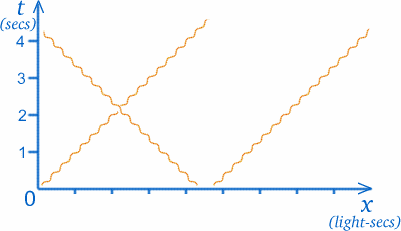
Den stora fördelen med detta är att en ljusstråles bana alltid kommer att vara i $45$ grader till axlarna. Detta innebär att en ljusstråle genom O kommer att stå i lika stora vinklar till båda axlarna, som du ser på diagrammet. (Även om ljuset färdas med konstant hastighet så att dess bana är en rät linje, representerar vi den med en vickande linje, som på bilden, för att skilja ljusstrålar från banor för andra föremål med massa.)
?

Mätning av tid

Vi har en tendens att anta att när människor är oense om vad klockan är, så är någons klocka fel, eller så kanske människorna befinner sig i olika tidszoner! Men det är ännu mer komplicerat än så! Enligt den speciella relativitetsteorin kan två personer befinna sig på samma plats och korrelera sina klockor, men om den ena rör sig i förhållande till den andra kommer de senare att vara oense om vad klockan är. tyvärr om du slår dig ihop med en vän och försöker testa den här teorin kommer du att bli besviken, inte för att teorin är felaktig, utan för att i den hastighet som du troligen kommer att kunna springa, även om du är en superidrottare, kommer effekten att vara för liten för att kunna observeras. Det är först när hastigheterna blir mycket stora (betydande bråkdelar av ljusets hastighet) som detta märkliga fenomen kan observeras, och även då endast med hjälp av extremt exakta klockor.
För att se hur detta skulle kunna fungera, låt oss betrakta ett ”tankeexperiment” som liknar det som Einstein föreslog. (Det är ett ”tankeexperiment” snarare än ett verkligt eftersom det inte går att genomföra, vilket du säkert inser). Anta att du tittar på klockan på Big Ben genom ett mycket kraftfullt teleskop, medan du rör dig bort från den på ett mycket snabbt tåg som passerade klockan exakt vid middagstid (jag vet att tåg inte passerar rakt förbi Big Ben, men låt oss låtsas!). Om tåget kunde röra sig med ljusets hastighet, vad skulle du då se hända med klockans visare? De skulle se ut att stå stilla, och båda pekar på $12$! Varför? Det beror på att det ljus som sänds ut av (eller reflekteras från) visarna vid middagstid skulle resa bort från klockan med exakt samma hastighet som du på tåget, och ljus som sänds ut vid senare tidpunkter skulle inte kunna hinna ikapp tåget! Märkligt!
Förstår du varför detta är ett ”tankeexperiment” (bortsett från det faktum att tåg inte passerar Big Ben)? Det beror på att ett tåg faktiskt inte skulle kunna röra sig med ljusets hastighet (vilket är något annat som den speciella relativitetsteorin säger oss – alla föremål som väger något kan aldrig röra sig lika snabbt som ljuset). Men anta att tåget rörde sig med halva ljusets hastighet (vilket fortfarande är mycket snabbt) – du skulle se klockans visare röra sig, men långsammare än visarna på din klocka! Tidsmätningen beror på hur du rör dig!
Hur kan detta vara möjligt? För att förstå detta kan vi betrakta en speciell sorts klocka, en ljusklocka . Det är inte troligt att du hittar en sådan vid din säng för att väcka dig på morgonen. Den består av en ljuskälla som sänder ut signaler som färdas en sträcka D och sedan reflekteras tillbaka till källan. Tidsgapet eller intervallet mellan varje gång en signal sänds ut och när den tas emot tillbaka definierar klockans tickar; de inträffar med $2T$ mellanrum, där \begin{ekvation} {T} = {D/c} \end{equation} där $c$ representerar ljusets hastighet. (Kom ihåg att hastighet = avstånd/tid, så tid = avstånd/hastighet.)

Nu antar vi att en rörlig raket bär en sådan klocka – besättningens erfarenhet kommer att vara att tickningarna sker med $2T$ mellanrum. Anta nu att besättningen på en stationär raket observerar klockan på den rörliga raketen och jämför den med sin egen, som också tickar med intervaller på $2T$. Vad kommer de att se? Diagrammen nedan bör ge svar på frågan. (Jag är ledsen att mina raketer ser mer ut som fiskar!)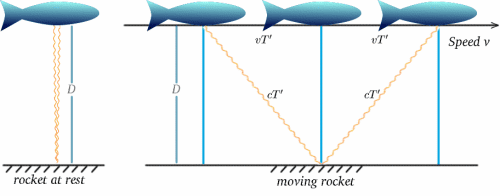
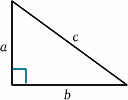
För den rörliga raketen reflekteras ljuset från spegeln på halva tiden mellan när signalen sänds och när den reflekteras tillbaka. Från den stationära raketen verkar restiden vara $2T^{ \prime}$ säg. Vi kan räkna ut detta med hjälp av en mycket viktig sats (ett fint namn för något som har bevisats vara sant inom matematiken!) – Pythagoras sats.

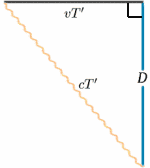\begin{ekvation} {a^2 + b^2} = {c^2} \quad (1) \end{equation} I raketdiagrammet har vi en rätvinklig triangel, så \begin{equation} D^2 + v^2 T^{’2} = {c^2 T ^{\prime 2}}\quad (2) \end{equation} Vi löser nu detta för $T^{\\prime}$: \begin{equation} {T^{\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \begin{equation} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{equation} vilket ger \begin{equation} {T^{\\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}}\quad (5) \end{equation} och så \begin{equation} {T^{\prime}}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}}, \quad (6) \end{equation} och klockfrekvenserna kommer att vara olika (om inte $v=0$). I själva verket är $T^{\prime}$$ större än $T$, så för den stationära besättningen ser det ut som om den rörliga klockan har längre intervaller mellan tickarna och därför går långsamt.
När vi väl har accepterat att det inte finns någon universell definition av tid som gäller för alla måste vi fundera på vad vi egentligen menar med att mäta tid. I någon mening mäter vi avstånd längs våra banor i rumtiden (tänk tillbaka på rumtidsdiagrammet). Tvillingarna följer olika vägar i rumtiden, så det är inte så förvånande att de har upplevt olika mängder tid.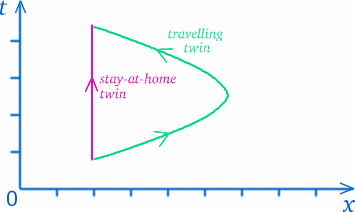
Men dra inga förhastade slutsatser – saker och ting är inte alltid vad de verkar…! Den resande tvillingens väg ser längre ut, men betyder det att hon har upplevt mer tid? För att se hur knepig den här typen av frågor är kan du tänka på en situation som kan vara ganska likartad. Anta att du bor i Trumpington, på södra sidan av Cambridge, och att du vill handla på Tesco’s i den norra delen av stadskärnan (så gott det går, utan att gå på gågator), på ringvägen eller på förbifarten – se diagrammet nedan.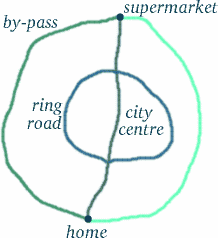
Under de flesta tider på dygnet skulle du märka att den längsta rutten – förbifarten – tar minst tid, följt av ringvägen. Är du nu övertygad om att det uppenbara svaret inte alltid är det rätta?
Vi har sett hur tid mäts med hjälp av ljussignaler. När vi har en exakt klocka kan vi sedan mäta avståndet med hjälp av ljus- eller radarsignaler som reflekteras från det avlägsna objektet; avståndet blir halva ljusets restid, multiplicerat med ljusets hastighet.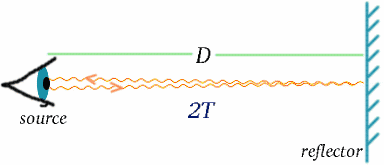

\begin{ekvation} {D} = {cT}\quad (7) \end{ekvation} Liksom tiden är avståndet en storhet där resultatet av mätningen beror på hur observatören rör sig.

K-faktorer

Jag ska nu beskriva en idé som ska hjälpa oss att göra beräkningar av den typ av effekt som jag har berättat om.
Antag att en astronaut B (för Ben) befinner sig i en raket som rör sig med hastigheten $c/5$ bort från en annan astronaut A (för Alf) på en rymdstation. En gång om året den 13 mars skickar Alf födelsedagshälsningar till Ben. Antag att radiomeddelandet med denna hälsning år 2010 uppmäts av rymdstationen att färdas ett halvt ljusår för att nå raketen och att det tar ett halvt år att göra detta. Nästa meddelande sänds exakt ett år senare. När denna radiosignal har rest ett halvt år till den plats där astronauten tog emot den föregående signalen har raketen rört sig ett femtedel ljusår längre bort, så denna signal måste resa längre för att hinna ikapp raketen. I själva verket är den tid som Alf mäter när signalen når raketen tre fjärdedelar av ett år efter det att den skickades – se diagrammet nedan. Stackars Alf drar slutsatsen att de födelsedagshälsningar som skickas varje år kommer att tas emot av Ben med ett och ett kvarts års mellanrum, enligt Alfs klocka.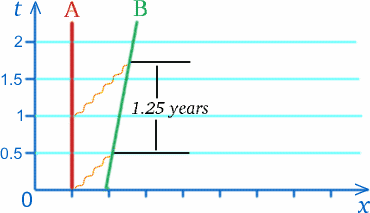
Detta säger oss inte vad Ben kommer att mäta för dessa intervaller, men det tyder på att det mycket väl inte kan vara ett år! En liknande effekt kommer att inträffa för signaler som skickas från Ben till Alf.
Nu ska vi titta på det allmänna fallet och göra detta mer exakt. Betänk två observatörer Alf och Ben som rör sig bort från varandra med konstanta hastigheter.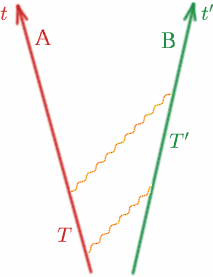
Alf skickar en ljussignal och sedan ytterligare en vid en tid $T$ senare. Ben tar emot de två signalerna vid tidpunkterna $T^{\prime}$ från varandra, enligt hans klocka. Då definierar vi en kvantitet $K$ genom \begin{ekvation} {K} = {T^{\prime}/T}. \quad (8) \end{equation} Observera att om Alf och Ben rörde sig med samma hastighet (i samma riktning!) skulle $K$ vara ett. Vi ska seelater exakt hur $K$ beror på Alf och Bens relativa hastighet. $K$ kallas ibland för dopplerförskjutningsfaktorn och effekten liknar den för ljudvågor – ni känner säkert alla till förändringen i ljudet av sirenen från en ambulans eller polisbil när den närmar sig och sedan avlägsnar sig.
Hur kan vi mäta $K$? Det uppenbara sättet är att observatörerna för register över när ljussignalerna sänds och tas emot så att de kan räkna ut $T$ och $T^{\prime}$$, och därmed $K$, när de träffas senare. En annan möjlighet är att den ena observatören har ett mycket kraftfullt teleskop med vilket han kan titta på den andra observatörens klocka (detta är verkligen tåget som kör förbi Big Ben igen!).
Vi måste göra några antaganden om detta tal $K$ för att det ska vara användbart för oss. Vi antar först att när Alf och Ben rör sig med konstanta hastigheter så beror $K$ inte på när $T$ och $T^{\prime}$ mäts, inte heller beror det på hur stor $T$ är. Om Alf till exempel väntar dubbelt så länge på att sända ljussignaler kommer $K$ att vara detsamma. Se om du kan fylla i siffrorna$T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ i det här fallet.
?

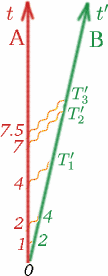
(Lägg märke till att det är okej att börja mäta tiden när de två observatörerna är tillsammans, och att de båda kan ställa in sina stoppklockor på noll vid det tillfället). Så i allmänhet har vi
?

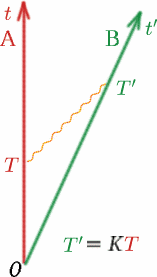
Den andra saken vi antar, som är lika viktig, är att den $K$ som Ben mäter för ljussignaler från Alf är densamma som den som Alf mäter för ljussignaler från Ben. Varför antar vi detta? Tänk dig två identiska bilar rygg mot rygg på en väg. Bilen $A$ står stilla och bilen $B$ kör iväg i en hastighet av $50 km/tim$ bort från $A$. Passagerare som tittar genom bakrutan på $A$ kommer att se $B$ försvinna i motsvarande takt. Passagerarna i $B$ kommer att se en mycket likartad bild om de tittar genom sitt bakre fönster – bil $A$ verkar röra sig iväg med samma hastighet! Har du någonsin haft den där kusliga upplevelsen att sitta i ett tåg och tro att det just har gått iväg, när det visar sig att det var granntåget som gick iväg i motsatt riktning och att ditt tåg fortfarande står stilla?
Detta antagande gör det möjligt för den ena observatören att mäta $K$ med hjälp av radar utan någon som helst medverkan från den andra observatören. Kan någon gissa hur? Låt mig ge dig en ledtråd.
Förutsätt som vanligt att Alf och Ben rör sig från varandra med konstant hastighet. Alf sänder ut två signaler med ett intervall på $T$, Ben reflekterar dem med intervallet $T^{\prime}$$ och Alf tar emot dem tillbaka igen med intervallet $T^{\prime\prime}$. Hur kan Alf räkna ut $K$?
?

Svar

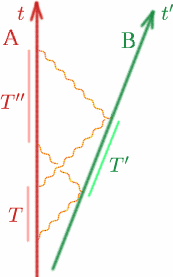
\begin{ekvation} {T^{\prime}} = {K T} \quad (9), \end{equation} \begin{equation} {T^{\\prime\prime}} = {K T^{{\prime}}\quad (10) \end{equation} Därför \begin{equation} {T^{\\prime\prime}} = {K(K T)} = {K^2 T}\quad (11) \end{equation} så vi har \begin{equation} {K} = {\sqrt{T^{\prime\prime}/T}}. \quad (12) \end{equation} Problem För att kunna utföra en komplicerad dockningsmanöver är det viktigt att två rymdfarkoster hålls i vila i förhållande till varandra. Utforma ett enkelt experiment för att kontrollera att så är fallet.

Sambandet mellan K och hastighet

Vi vet redan att om den relativa hastigheten för Alf och Ben är noll, så är $K$ = $1$. Vad är dess värde för allmänna hastigheter? Det finns ett smart sätt att räkna ut detta, som använder sig av den idé som vi just har talat om, plus idén om simultanitet. Vad innebär det? Jag ska förklara om det om en minut.
Först ska vi föreställa oss våra vanliga två observatörer som reser bort från varandra med konstant hastighet $v$. Låt oss anta att när de är tillsammans ställer de båda sina klockor till $t = 0$. Vid tiden $T$ enligt hans klocka sänder Alf ut en radiosignal; Ben reflekterar den tillbaka vid tiden $T’$ enligt hans klocka och Alf får tillbaka den igen vid tiden $T^{\prime\prime}$ enligt hans klocka. Låt oss rita en bild som vanligt.
?

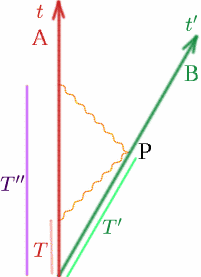
Nu vet vi att \begin{ekvation} {T^{\prime}}} = {K T}\kvad (13) \end{ekvation} \begin{ekvation} {T^{\\prime\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{equation} Alf tror alltså att restiden för radiopulsen är \begin{ekvation} {T^{\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{ekvation} och Alf räknar ut att avståndet, $D$, mellan honom själv och Ben är halva den sträcka som radiosignalen tillryggalägger, vilket är halva hastigheten gånger tiden: \begin{ekvation} {D} = {\frac {1} {2} c(K^2-1)T}. \kvad (16) \end{ekvation} Nu vet vi att avståndet mellan Alf och Ben ständigt förändras, så vi måste fråga oss när (dvs. vid vilken tidpunkt) detta är avståndet mellan Alf och Ben. Det är här vi behöver idén om simultanitet. Avståndet mäts tydligt när Ben befinner sig i punkten $P$, men vilken tid motsvarar detta för Alf? Alf vet att radiopulsen färdas lika långt ut och tillbaka, så händelsen $Q$, som Alf bedömer vara vid samma tidpunkt som $P$, kommer att vara halvvägs mellan $T$ och $T^{\prime\prime}$. (Vi säger att $Q$ är samtidigt med $P$ för Alf – det betyder bara samtidigt). Så tiden vid $Q$ är \begin{ekvation} {T_Q} = {\frac {1} {2}(T+T”)} = {\frac {1} {2} (K^2+1)T}}}. \quad (17) \end{equation} Alf drar alltså slutsatsen att Ben har tillryggalagt en sträcka $D$ på tiden $T_Q$, så hans hastighet $v$ ges av \begin{equation} {v} = {\frac {D} {T_Q}} = {\frac {\frac {\frac {1}} {\frac {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \quad (18) \end{ekvation} Därför har vi \begin{ekvation} {\frac {v} {c}}} = {\frac {K^2-1} {K^2+1}}}. \quad (19) \end{equation} Vi kan nu räkna ut $K$ i termer av $\frac {v} {c}$: \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c}} + \frac{v}{c}}} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Därför \begin{equation} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}}\quad (23) \end{equation} och så \begin{equation} {K} = \sqrt{{\left({\frac{1+\frac{v}{c}{c}}}{1-\frac{v}{c}}}\right)}}. \quad (24) \end{ekvation} Prova att räkna ut några värden på K:
till exempel $v = c/4$ – det ger $K = \sqrt{5/3} = 1,291$.
Prova nu $v = c/2, 9c/10, 99c/100$.
Nu spelar det ingen roll om Alf står stilla och Ben rör sig eller tvärtom – $K$ är fortfarande densamma. Det som är annorlunda är om Alf och Ben närmar sig varandra snarare än rör sig från varandra – i det fallet tar vi värdet av $v$ som negativt, men vi kan använda samma formel.
T.ex. om Alf och Ben närmar sig varandra med relativ hastighet $c/2$, \begin{equation} K = \sqrt{{\left({\frac{1+(-1/2)}{1-(-1/2)}}\right)}} = \sqrt{{\left({\frac{1/2}{3/2}}\right)}} = \sqrt{1/3}. \quad (25) \end{ekvation}. Låt oss räkna ut $K$ för några typiska hastigheter:
1) flygplan som närmar sig varandra med en hastighet på 1000 km/tim$;
2) galaxer i vårt kluster som rör sig från varandra med relativa hastigheter på 500 km/s$;
3) en bil som närmar sig en polis med en hastighet på 100 km/tim$;
4) du som går mot din vän med en hastighet på 5 km/tim$ Tror du att någon av dessa effekter skulle vara observerbara? Tvillingparadoxen – äntligen!
Vad händer? Varför är det en paradox? (Vad betyder ordet paradox egentligen?)
Låt oss tänka på enäggstvillingarna Albertina och Brigitta! Albertina stannar hemma i London medan Brigitta, den äventyrliga tvillingen, åker på en rymdresa. Hon reser bort från jorden i 6 år, mätt med hennes klocka, i ett mycket snabbt rymdskepp som färdas med $v = 4c/5$. Hon återvänder sedan med samma hastighet i 6 år. Brigitta mäter alltså en tid på 12 år för sin resa – hon är 12 år äldre när hon kommer hem till Albertina i London. Men hur mycket äldre är Albertina? Låt oss se om din gissning var rätt eller kanske bara nära!
Låt oss rita ett rymdtidsdiagram: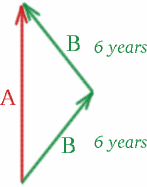
På Brigittas resa utåt rör sig tvillingarna isär med relativ hastighet $v = 4c/5$, så \begin{ekvation} {K^2} = {\frac{1+\frac{4}{5}}}{1-\frac{4}{5}}} = {9}, \quad (26) \end{ekvation} och vi har $K=3$. På Brigittas återresa närmar de sig varandra med samma hastighet, så \begin{ekvation} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}}\quad (27) \end{ekvation} och $K=1/3$. Allt vi behöver göra för att räkna ut den tid som Albertina mäter är att sätta in en ljussignal! Några förslag på var?
Antag att Albertina sänder en signal vid punkten $S$$, som väljs så att den når Brigitta vid $U$, precis när hon är på väg att vända om.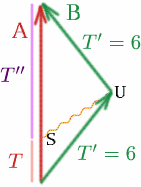
Vad är då $T$ om $T^{\prime}=6$ och $K=3$? Vi har \begin{ekvation} {T^{\\prime}} = {K T} \quad (28) \end{equation}
så $6=3T$ och $T=2$.
Se nu på vad som händer på Brigittas hemresa. Vad är $T^{\\prime\prime}$? Vi har $T^{\prime}=6$, $K=1/3$ och \begin{ekvation} {T^{\prime}} = {K T^{\prime\prime}}, \quad (29) \end{ekvation} så $6=T^{\prime\prime}/3$ och $T^{\prime\prime}=18$. Därför är den totala tid som Albertina mäter $T+T^{{\prime\prime}=20$ år, så hon är 20 år äldre när de träffas, medan Brigitta bara är 12 år äldre! Albertina har alltså åldrats 8 år mer än Brigitta!
Så gissade du rätt????
Vad du kan försöka göra på egen hand är några experiment med siffror. Du kan till exempel föreställa dig att Brigitta gör en resa på 10+10=20$ år, och du kan räkna ut hur snabbt hon måste resa för att Albertina ska ha åldrats med bara ett år mer än hon (dvs. 21$ år har gått på Albertinas klocka) när Brigitta återvänder. Kanske kan du räkna ut om det skulle vara möjligt att göra en realistisk (dvs. genomförbar) rymdresa under vilken tvillingar skulle åldras olika mycket!
Nu varför kallas allt detta för en paradox? Minns du vad paradox betyder? Vi sa tidigare att om två personer rör sig med konstanta hastigheter (och därmed konstanta hastigheter i förhållande till varandra) är mycket av det som händer detsamma oavsett om vi betraktar den första som stationär och den andra som rör sig, eller tvärtom. Om vi tillämpar det argumentet på Albertina och Brigitta, varför kan vi då inte betrakta Brigitta i sitt rymdskepp som den person som sitter stilla, och Albertina på jorden som seglar iväg och sedan kommer tillbaka. Det låter ganska fånigt, men jag hoppas att ni förstår vad jag menar. Då skulle vi förvänta oss att Brigitta är äldre än Albertina när de slutligen möts. Men vi har redan sagt att Albertina är äldre då. Hur kan båda dessa påståenden vara sanna? Det är paradoxen!
Kan du se vad som är fel?
Punkten är att Brigitta inte rör sig med konstant hastighet i förhållande till Albertina under hela sin resa; hon har två långa reseavsnitt där hon gör det, men däremellan finns det ett möjligen kort men mycket viktigt avsnitt där hon saktar ner, stannar och sedan accelererar i motsatt riktning. Acceleration är ett verkligt fenomen, vilket ni säkert känner till från de åkattraktioner som får er att må illa på ett tivoli! Vet du hur det kan upptäckas med en enkel utrustning?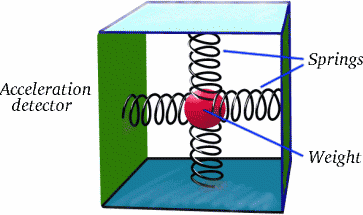
Och vad tycker du om allt detta? Det verkar lite orättvist att Brigitta får resa och se mer av universum men blir yngre än sin tvillingsyster som stannar hemma – livet är inte alltid rättvist! Men det borde uppmuntra dig att resa – inte nödvändigtvis i rymden! – och vara äventyrlig! Referens För mer information om tvillingparadoxen och de tekniker som beskrivs här kan du försöka läsa boken Flat and Curved Space-Times , av G. F. R. Ellis och mig själv (utgiven av Oxford University Press 1988). Du kan också titta på Mr Tompkins-böckerna som introducerar den speciella relativitetsteorins begrepp på ett underhållande och lättillgängligt sätt.

Du kan hitta recensioner av Mr Tompkins-böckerna och beställa dem från Cambridge University Press hemsida, till exempel se The New World of Mr Tompkins : George Gamow’s Classic Mr Tompkinsin Paperback