Inleiding

Als u dit project volgt, zult u tot een verbazingwekkende conclusie komen! Stel dat een van een paar eeneiige tweelingen een ruimtereis maakt en dan terugkeert om zijn of haar (laten we zeggen haar) leeftijd te vergelijken met die van de andere tweeling die op dezelfde plaats op aarde is gebleven. Het blijkt dat na de reis de ene tweeling jonger zal zijn dan haar zus! Je vraagt je vast af hoe dat kan, en het doel van dit project is om je te laten zien hoe dat kan.
Laten we beginnen met een raadspelletje – aan het eind zullen we zien of je het bij het rechte eind hebt! Stel dat de reizende tweeling een reis van 12 jaar maakt – 6 jaar heen en 6 jaar terug. Het is duidelijk dat ze 12 jaar ouder zal zijn als ze terugkomt. Wat je moet doen is raden hoeveel ouder de niet reizende tweeling zal zijn….! Ik moet je vertellen hoe snel de bewegende tweeling reist – laten we zeggen viervijfde van de lichtsnelheid – hoewel ik durf te zeggen dat dit je niet veel zal helpen met je gok! Ik stel voor dat u een geheel getal tussen 1 en 30 raadt! Voordat we de tweeling bekijken, moeten we een aantal hulpmiddelen instellen die we nodig zullen hebben om te begrijpen wat er aan de hand is. We zullen veel gebruik maken van een soort grafiek, het ruimte-tijd diagram. Maakt u zich geen zorgen als u nog nooit grafieken hebt gebruikt – we zullen proberen bij de basis te beginnen.
?

Grafieken

De eenvoudigste soort grafiek is gewoon een afbeelding van wat er gebeurt op een gekozen plat oppervlak. Laten we aannemen dat u aan een tafel of een bureau zit, en dat u twee linialen en een groot stuk papier hebt. Begin in de linker benedenhoek en leg één liniaal langs de onderkant en één langs de linkerkant omhoog, met het papier ertussen in positie. Het resultaat ziet er dan als volgt uit:

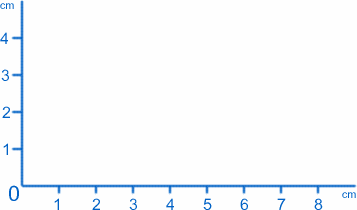
Wij noemen het punt waar de twee linialen elkaar raken (het nulpunt op beide schalen) de oorsprong, kortweg O, en de linialen de twee assen. Volgens afspraak noemen we de as langs de onderkant de x-as, en die langs de zijkant de y-as. We kunnen elk punt op het papier labelen met de waarden van $x$ en $y$. De oorsprong heeft bijvoorbeeld $x=0$, $y=0$. Het punt $1cm$ van de y-as en $2cm$ van de x-as heeft $x=1$, $y=2$ (ik heb ze echt goed omgedraaid!).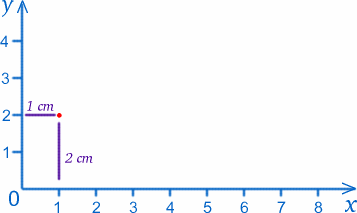

Oefening Teken je eigen grafiek en markeer de volgende punten:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Welke vorm vormen ze?
Stel je nu een paar mieren voor met heel vuile voeten. Stel dat er een over het papier loopt en steeds op een afstand van $1cm$ van de x-as blijft. Zijn pad zou een lijn zijn, beschreven door de vergelijking $y=1$ (een mooie manier om te zeggen wat in de vorige zin in woorden is gezegd). Een andere mier loopt misschien altijd 3cm$ van de y-as af; de vergelijking van zijn pad is dan $x=3$. Een wat originelere mier zou zo kunnen lopen dat zijn afstand tot beide assen altijd gelijk is; hij zou door $x=1$, $y=1$; $x=2$, $y=2$; enzovoort gaan en zijn pad zou worden gegeven door de vergelijking $x=y$.

Ruimte-tijd diagrammen

In dit gedeelte zullen we enkele grafieken tekenen die erg lijken op die in het vorige gedeelte, maar hun betekenis zal nogal verschillend zijn. We hebben nog steeds twee assen, en de as met het opschrift $x$ geeft nog steeds de afstand in een bepaalde richting aan. Stel je bijvoorbeeld een bal voor op een vast punt op 3 cm van O; zijn pad in de ruimte-tijd zal de rechte lijn $x=3$ zijn. Stel nu dat de bal over een recht pad rolt; dan zouden punten op de grafiek overeenkomen met posities van de bal op bepaalde tijdstippen, b.v. $x=5$, $t=4$ zou overeenkomen met het feit dat de bal $5cm$ van de oorsprong is $4$ seconden nadat de tijdmeting begon.
Oefening Plot punten op de grafiek die overeenkomen met de volgende gebeurtenissen in de geschiedenis van de bal: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Hoe zou je dit interpreteren?
Probeer nu $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Wat valt je op aan deze punten?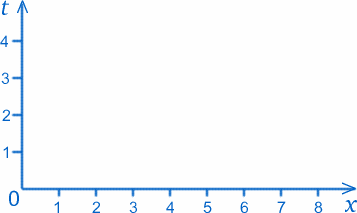
Als het pad van de bal een rechte lijn is op de grafiek, betekent dit dat de bal met constante snelheid beweegt (misschien snelheid nul). In dat geval kunnen we de snelheid berekenen door te kijken hoe ver de bal in één seconde aflegt – we delen de verandering in de x-waarde door de overeenkomstige verandering in de t-waarde. In ons tweede voorbeeld is de snelheid van de bal dus $2cm/sec$. Ben je het daarmee eens?
Oefening Teken een grafiek van de beweging van een bal die heen en weer beweegt tussen twee punten, met constante snelheid (maar natuurlijk wel regelmatig van richting veranderend).
We gaan nu iets tamelijk vreemds doen met onze grafiek. In de speciale relativiteitstheorie, die het interessant maakt om na te denken over tweelingen en ruimtereizen, moeten we vaak lichtstralen op onze grafieken plotten. Nu reizen lichtstralen in de lege ruimte met een constante en zeer grote (maar eindige) snelheid; een lichtstraal die jou vanuit de zon bereikt, is daar ongeveer $8$ minuten geleden vertrokken. (Vroeger dacht men dat licht oneindig snel ging, zodat je de sterren kon zien op het moment dat je ze waarnam, maar nu weet men dat dit niet klopt). Om precies te zijn, de snelheid van het licht is ongeveer $30000000000cm/sec$! Dit zou kunnen leiden tot een aantal zeer vreemde schalen op de assen van een ruimte-tijd grafiek, dus zullen we ervoor kiezen om afstand op een andere manier te meten; de eenheden op de x-as zullen lichtseconden zijn, d.w.z. de afstand afgelegd door het licht in één seconde. (Als de schaal voor $t$ jaren is, zal de overeenkomstige x-schaal lichtjaren zijn).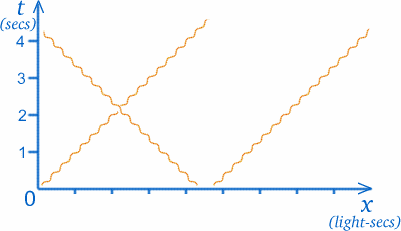
Het grote voordeel hiervan is dat het pad van een lichtstraal altijd $45$ graden ten opzichte van de assen zal staan. Dit betekent dat een lichtstraal door O een gelijke hoek met beide assen zal maken, zoals je op het diagram ziet. (Hoewel licht met constante snelheid reist en zijn pad dus een rechte lijn is, stellen we het voor met een kronkelige lijn, zoals afgebeeld, om lichtstralen te onderscheiden van paden van andere voorwerpen met massa.)
?

Het meten van tijd

We zijn geneigd aan te nemen dat wanneer mensen het niet eens zijn over hoe laat het is, iemands horloge verkeerd is, of dat de mensen misschien in verschillende tijdzones zitten! Maar het is nog ingewikkelder dan dat! Volgens de speciale relativiteit kunnen twee mensen op dezelfde plaats zijn en hun horloges met elkaar correleren, maar als de een beweegt ten opzichte van de ander, zullen ze het vervolgens oneens zijn over hoe laat het is.Helaas, als u samen met een vriend probeert deze theorie te testen, zult u teleurgesteld zijn, niet omdat de theorie onjuist is, maar omdat bij de snelheid die u waarschijnlijk zult kunnen lopen, zelfs als u een superatleet bent, het effect te klein zal zijn om waar te nemen. Het is slechts wanneer de snelheden zeer groot worden (aanzienlijke fracties van de lichtsnelheid) dat dit vreemde fenomeen kan worden waargenomen en, zelfs dan, slechts door het gebruik van uiterst nauwkeurige klokken.
Om te zien hoe dit zou kunnen werken, laat ons een “gedachte-experiment” beschouwen gelijkaardig aan datgene wat Einstein voorstelde. (Het is eerder een “gedachte”-experiment dan een echt experiment, omdat het niet echt kan worden uitgevoerd, zoals u zult beseffen). Stel dat je door een zeer krachtige telescoop naar de klok op de Big Ben kijkt, terwijl je je ervan verwijdert met een zeer snelle trein die precies om 12 uur langs de klok rijdt (ik weet dat treinen niet vlak langs de Big Ben rijden, maar laten we doen alsof!). Als de trein zich met de snelheid van het licht zou kunnen voortbewegen, wat zou je dan zien gebeuren met de wijzers van de klok? Ze zouden stil lijken te staan en allebei naar $12$ wijzen! Waarom? Omdat het licht dat ’s middags door de wijzers wordt uitgezonden (of door de wijzers wordt weerkaatst) met precies dezelfde snelheid van de klok weg zou reizen als u in de trein, en het licht dat op latere tijdstippen wordt uitgezonden de trein niet zou kunnen inhalen! Vreemd!
Begrijpt u nu waarom dit een “gedachte-experiment” is (nog afgezien van het feit dat treinen niet langs de Big Ben rijden)? Het is omdat een trein zich in feite niet met de snelheid van het licht kan voortbewegen (dat is iets anders dat de speciale relativiteit ons vertelt – elk voorwerp dat iets weegt kan zich nooit zo snel als het licht voortbewegen). Maar stel dat de trein zich met de helft van de lichtsnelheid voortbewoog (nog steeds erg snel) – dan zou je de wijzers van de klok zien bewegen, maar langzamer dan die op je horloge! Het meten van de tijd hangt af van hoe je beweegt! Hoe kan dat? Laten we, om dit te begrijpen, eens kijken naar een speciaal soort klok, een lichtklok. Het is niet waarschijnlijk dat u zo’n klok naast uw bed vindt om u ’s morgens wakker te maken. Hij bestaat uit een lichtbron die signalen uitzendt die een afstand D afleggen en dan naar de bron worden teruggekaatst. Het tijdsinterval tussen het uitzenden van een signaal en het terugontvangen ervan bepaalt het tikken van de klok; dit gebeurt met een tussenpoos van $2T$, waarbij \begin{equation} {T} = {D/c} \waarbij $c$ de lichtsnelheid is. (Bedenk dat snelheid = afstand/tijd, dus tijd = afstand/snelheid.)

Nemen we nu aan dat een bewegende raket zo’n klok draagt – de ervaring van de bemanning zal zijn dat de tikken met tussenpozen van $2T$ voorkomen. Stel nu dat de bemanning van een stilstaande raket de klok van de bewegende raket observeert en vergelijkt met hun eigen klok, die ook met tussenpozen van $2T$ tikt. Wat zullen zij zien? De diagrammen hieronder zouden het antwoord moeten suggereren. (Het spijt me dat mijn raketten meer op vissen lijken!)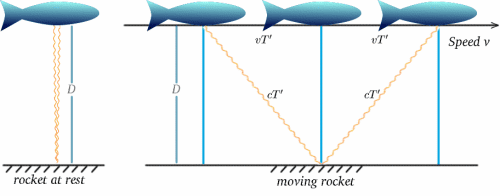
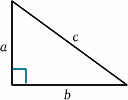
Voor de bewegende raket wordt het licht door de spiegel weerkaatst op de helft van de tijd tussen het moment waarop het signaal wordt uitgezonden en het moment waarop het wordt teruggekaatst. Voor de stilstaande raket lijkt de reistijd $2T^{ \prime}$ te zijn. We kunnen dit uitrekenen met behulp van een zeer belangrijke stelling (een mooie naam voor iets waarvan in de wiskunde is bewezen dat het waar is!) – die van Pythagoras.

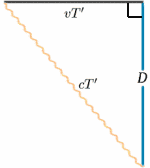\^quad (1) ^eend{equation} In het diagram van de raket hebben we een rechthoekige driehoek, dus begin{equation} D^2 + v^2 T^{‘2} = {c^2 T ^{primeur 2}} {quad (2) \end{equation} We lossen dit nu op voor $T^{{‘prime}$: \{T^{\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \begin{equation} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \eind{equation}, zodat begin{equation} {T^{prime}} = {{D}} {c \sqrt{(1 – v^2/{c^2})}}, \quad (5) \end{equation} en dus \begin{equation} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}}, \quad (6) \end{equation} en de kloksnelheden zullen verschillend zijn (tenzij natuurlijk $v=0$). In feite is $T^{eenvoud}$ groter dan $T$, zodat het voor de stilstaande bemanning lijkt alsof de bewegende klok langere intervallen tussen de tikken heeft en dus langzaam gaat.
Als we eenmaal accepteren dat er geen universele definitie van tijd is die voor iedereen geldt, moeten we nadenken over wat we werkelijk bedoelen met het meten van tijd. In zekere zin meten we afstanden langs onze paden in de ruimte-tijd (denk terug aan het ruimte-tijd diagram). De tweeling volgt verschillende paden in de ruimte-tijd, dus is het niet zo verwonderlijk dat zij verschillende hoeveelheden tijd hebben ervaren.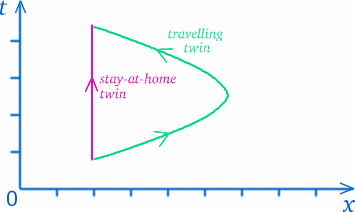
Maar trek niet te snel conclusies – dingen zijn niet altijd wat ze lijken…! Het pad van de reizende tweeling lijkt langer, maar betekent dat dat zij meer tijd heeft meegemaakt? Om te zien hoe lastig dit soort vragen is, denk eens aan een situatie die er wel eens op zou kunnen lijken. Stel dat u in Trumpington woont, aan de zuidkant van Cambridge, en boodschappen wilt doen bij Tesco’s aan de noordkant van het stadscentrum (zo goed als u kunt, voetgangerszones vermijdend), op de ringweg of op de rondweg – zie het schema hieronder.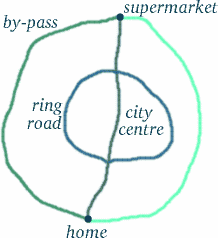
Op de meeste momenten van de dag zou u merken dat de langste route – de rondweg – de minste tijd kost, gevolgd door de ringweg. Ben je er nu van overtuigd dat het voor de hand liggende antwoord niet altijd het juiste is?
We hebben gezien hoe de tijd wordt gemeten met behulp van lichtsignalen. Als we eenmaal een nauwkeurige klok hebben, kunnen we de afstand meten met licht- of radarsignalen die door het verre voorwerp worden weerkaatst; de afstand is dan de helft van de reistijd van het licht, vermenigvuldigd met de lichtsnelheid.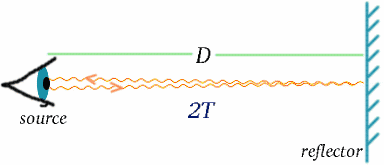

>Begin{equation} {D} = {cT}}quad (7) \end{equation} Net als tijd is afstand een grootheid waarbij het resultaat van de meting afhangt van de manier waarop de waarnemer beweegt.

K-factoren

Ik ga nu een idee beschrijven dat ons moet helpen berekeningen uit te voeren van het soort effect waarover ik jullie heb verteld.
Voorstel dat een astronaut B (voor Ben) zich in een raket met snelheid $c/5$ verwijdert van een andere astronaut A (voor Alf) in een ruimtestation. Eens per jaar op 13 maart stuurt Alf een verjaardagsgroet naar Ben. Stel dat de radioboodschap met deze groet in het jaar 2010 volgens de metingen van het ruimtestation een afstand van een half lichtjaar moet afleggen om de raket te bereiken, en daar een half jaar over doet. Het volgende bericht wordt precies een jaar later verzonden. Wanneer dit radiosignaal een half jaar heeft gereisd tot waar Ben de astronaut het vorige signaal ontving, is de raket een vijfde lichtjaar verder, zodat dit signaal langer moet reizen om de raket in te halen; in feite is de door Alf gemeten tijd wanneer het signaal de raket bereikt driekwart jaar nadat het werd verzonden – zie het diagram hieronder. De arme Alf concludeert dat de verjaardagsgroeten die jaarlijks worden verzonden, door Ben zullen worden ontvangen met tussenpozen van een en een kwart jaar, volgens Alf’s klok.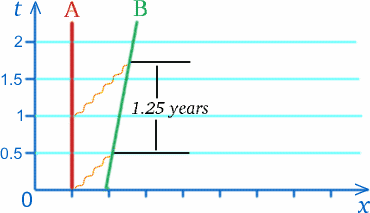
Dit vertelt ons niet wat Ben voor deze intervallen zal meten, maar het suggereert wel dat het wel eens geen jaar zou kunnen zijn! Een soortgelijk effect zal optreden voor signalen die van Ben naar Alf worden gezonden.
Nu gaan we naar het algemene geval kijken en dit nauwkeuriger maken. Beschouw twee waarnemers, Alf en Ben, die zich met constante snelheid van elkaar verwijderen.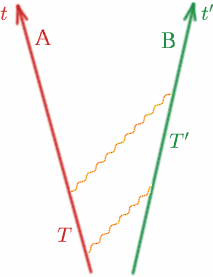
Alf zendt een lichtsignaal en vervolgens nog een op tijdstip $T$ later. Ben ontvangt de twee signalen op een tijdstip dat volgens zijn klok $T^{prime}$ verschilt. Dan definiëren we een grootheid $K$ door {K} = {T^{\prime}/T}. \quad (8) \eind{equation} Merk op dat als Alf en Ben met dezelfde snelheid (in dezelfde richting!) zouden bewegen, $K$ één zou zijn. We zullen later precies zien hoe $K$ afhangt van de relatieve snelheid van Alf en Ben. $K$ wordt ook wel de Doppler-verschuivingsfactor genoemd en het effect is vergelijkbaar met dat van geluidsgolven – u kent vast allemaal de verandering in geluid van de sirene van een ambulance of politieauto als die nadert en dan weer wegtrekt.
Hoe kunnen we $K$ meten? De meest voor de hand liggende manier is dat de waarnemers bijhouden wanneer de lichtsignalen worden uitgezonden en ontvangen, zodat ze later bij een ontmoeting $T$ en $T^{prime}$, en dus $K$, kunnen uitrekenen. Een andere mogelijkheid is dat de ene een zeer krachtige telescoop heeft waarmee hij de klok van de andere in de gaten kan houden (dit is eigenlijk weer de trein die langs de Big Ben rijdt!).
We moeten enkele veronderstellingen maken over dit getal $K$ om het voor ons nuttig te laten zijn. We nemen eerst aan dat wanneer Alf en Ben met constante snelheid bewegen, dat $K$ niet afhangt van wanneer $T$ en $T^{prime}$ gemeten worden, en ook niet van hoe groot $T$ is. Dus als Alf bijvoorbeeld twee keer zo lang wacht met het versturen van lichtsignalen, zal $K$ hetzelfde zijn. Kijk of je de getallen $T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ in dit geval kunt invullen.
?

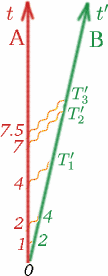
(Merk op dat het OK is om de tijd te beginnen meten als de twee waarnemers samen zijn, en ze kunnen allebei hun stopwatches op dat moment op nul zetten). In het algemeen hebben we dus
?

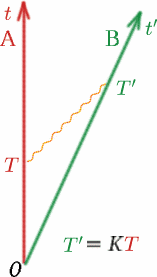
Het tweede dat we aannemen, en dat is even belangrijk, is dat de $K$ die Ben meet voor lichtsignalen van Alf dezelfde is als die Alf meet voor lichtsignalen van Ben. Waarom nemen we dit aan? Stel je twee identieke auto’s rug aan rug op een weg voor. Auto $A$ blijft stilstaan en auto $B$ rijdt weg met een snelheid van $50 km/uur$ weg van $A$. Passagiers die door de achterruit van $A$ kijken, zullen $B$ met de juiste snelheid zien verdwijnen. Passagiers in $B$ zullen een zeer vergelijkbaar beeld zien als ze door hun achterruit kijken – auto $A$ zal met dezelfde snelheid weg lijken te rijden! Heeft u wel eens de griezelige ervaring gehad dat u in een trein zat en dacht dat die net wegreed, terwijl het de naburige trein bleek te zijn die in tegengestelde richting wegreed en uw trein nog steeds stilstaat?
Deze veronderstelling maakt het voor de ene waarnemer mogelijk om $K$ met radar te meten zonder enige medewerking van de andere. Kan iemand raden hoe? Ik zal u een hint geven.
Voorstel zoals gewoonlijk dat Alf en Ben met constante snelheid uit elkaar bewegen. Alf zendt twee signalen uit met een interval van $T$, Ben weerkaatst ze met een interval van $T^{prime}$ en Alf ontvangt ze weer terug met een interval van $T^{prime}$. Hoe kan Alf $K$ uitrekenen?
?

Antwoord

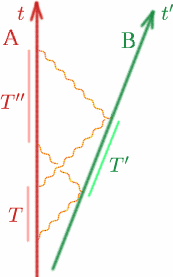
Begin{equation} {T^{\prime}} = {K T} \kwadraat (9), einde \begin{equation} {T^{\prime}} = {K T^{\prime}} kwadraat (10) einde{equation} Daarom is \begin{equation} {T^{\prime}} = {K(K T)} = {K^2 T}}}quad (11) \end{equation} dus hebben we \begin{equation} {K} = {\sqrt{T^{\prime}/T}}. \kwadraat (12) einde{equation} Probleem Om een ingewikkeld koppelmanoeuvre uit te voeren, is het essentieel dat twee ruimtevaartuigen ten opzichte van elkaar in rust zijn. Bedenk een eenvoudig experiment om na te gaan of dit zo is.

Het verband tussen K en snelheid

We weten al dat als de relatieve snelheid van Alf en Ben nul is, dan $K$ = $1$. Wat is de waarde ervan voor algemene snelheden? Er is een slimme manier om dit uit te werken, die gebruik maakt van het idee waar we het net over hadden, plus het idee van gelijktijdigheid. Wat houdt dat in? Ik zal het zo uitleggen.
Stellen we ons eerst onze gebruikelijke twee waarnemers voor die met constante snelheid $v$ van elkaar weg bewegen. Laten we aannemen dat wanneer ze samen zijn, ze allebei hun klok op $t = 0$ zetten. Op tijdstip $T$ volgens zijn klok zendt Alf een radiosignaal uit; Ben kaatst het terug op tijdstip $T’$ volgens zijn klok en Alf krijgt het weer terug op tijdstip $T^{prime}$ volgens zijn klok. Laten we zoals gewoonlijk een tekening maken.
?

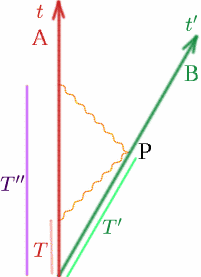
Nu weten we dat \begin{equation} {T^{prime}} = {K T}}quad (13) \end{equation} \Begin {quad} {T^{\prime}} = {K T^{\prime}} = {K^2 T}}. \^quad (14) ^eind{equation} Alf denkt dus dat de reistijd van de radiopuls de helft is van de afstand die het radiosignaal heeft afgelegd, dat is de helft van de snelheid maal de tijd: \Begin {quation} {D} = {\frac {1} {2} c(K^2-1)T}. \(16) Einde{equation} Nu weten we dat de afstand tussen Alf en Ben voortdurend verandert, dus moeten we ons afvragen wanneer (d.w.z. op welk tijdstip) dit de afstand tussen Alf en Ben is. Hier hebben we het idee van simultaniteit nodig. De afstand wordt duidelijk gemeten wanneer Ben op het punt $P$ is, maar met welk tijdstip komt dit overeen voor Alf? Wel, Alf weet dat de radiopuls dezelfde afstand heen en terug aflegt, dus de gebeurtenis $Q$, waarvan Alf oordeelt dat die op hetzelfde moment is als $P$, zal halverwege tussen $T$ en $T^{prime}$ liggen. (We zeggen dat $Q$ voor Alf gelijktijdig is met $P$ – het betekent gewoon op hetzelfde moment). Dus de tijd op $Q$ is begin{equation} {T_Q} = {\frac {1} {2}(T+T”)} = {\frac {1} {2} (K^2+1)T}. \Einde{equation} Alf concludeert dus dat Ben in tijd $T_Q$ een afstand $D$ heeft afgelegd, zodat zijn snelheid $v$ gegeven wordt door \begin{equation} {v} = {\frac {D}} {T_Q}} = {\frac {\frac {1}} {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \Einde{equation} Daarom geldt dat {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \{quadr(19)} {einde{quadr} We kunnen nu $K$ uitrekenen in termen van $\frac {v} {c}$: \{begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \{K^2 \frac{v}{c}} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Dus begin {quation} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}} {quad (23) \end{equation}} en dus \begin{equation} {K} = \sqrt{ {links({\frac{1+ \frac{v}{c}}{1- \frac{v}{c}}}}} rechts)}}. \Einde {quad (24) Probeer enkele waarden van K uit te rekenen:
bijvoorbeeld $v = c/4$ – dat geeft $K = \sqrt{5/3} = 1,291$.
Probeer nu eens $v = c/2, 9c/10, 99c/100$.
Nu maakt het niet uit of Alf stilstaat en Ben beweegt of andersom – $K$ is nog steeds hetzelfde. Wat anders is, is als Alf en Ben elkaar naderen in plaats van uit elkaar te bewegen – in dat geval nemen we de waarde van $v$ als negatief, maar we kunnen dezelfde formule gebruiken.
Bijv. als Alf en Ben elkaar naderen met relatieve snelheid $c/2$, dan geldt K = \sqrt{{links({\frac{1+(-1/2)}{1-(-1/2)}}}} = \sqrt{{links({\frac{1/2}{3/2}}}} = \sqrt{1/3}. \Einde citaat (25). Laten we $K$ eens berekenen voor enkele typische snelheden:
1) vliegtuigen die elkaar naderen met een snelheid van $1000km/uur$;
2) melkwegstelsels in onze cluster die uit elkaar bewegen met relatieve snelheden van $500km/s$;
3) een auto die een politieagent nadert met een snelheid van $100km/uur$;
4) jij die naar je vriend toe loopt met een snelheid van $5km/uur$ Denk je dat een van deze effecten waarneembaar zou zijn? De tweelingparadox – eindelijk! Wat gebeurt er? Waarom is het een paradox? (Wat betekent het woord paradox eigenlijk?)
Laten we eens kijken naar een eeneiige tweeling, Albertina en Brigitta! Albertina blijft thuis in Londen, terwijl Brigitta, de avontuurlijke, op ruimtereis gaat. Zij reist 6 jaar weg van de Aarde, gemeten met haar klok, in een zeer snel ruimteschip dat reist met $v = 4c/5$. Daarna keert ze met dezelfde snelheid gedurende 6 jaar terug. Brigitta meet dus een tijd van 12 jaar voor haar reis – ze is 12 jaar ouder als ze weer thuiskomt bij Albertina in Londen. Maar hoeveel ouder is Albertina? Laten we eens kijken of je gok juist was of misschien er net naast!
Laten we een ruimte-tijd diagram tekenen: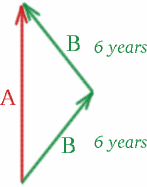
Op de heenreis van Brigitta beweegt de tweeling zich met een relatieve snelheid van $v = 4c/5$ uit elkaar, zodat {K^2} = {\frac{1+\frac{4}{5}}{1-\frac{4}{5}} = {9}, \quad (26) \end{equation} en we hebben $K=3$. Op de terugreis van Brigitta naderen ze elkaar met dezelfde snelheid, dus \begin{equation} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}}quad (27) \eind{equation} en $K=1/3$. Het enige wat we moeten doen om de tijd te berekenen die Albertina meet is een lichtsignaal plaatsen!
Stel dat Albertina een signaal zendt op het punt $S$, dat zo is gekozen dat het Brigitta op $U$ bereikt, net op het moment dat zij op het punt staat zich om te draaien.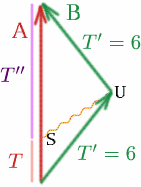
Wat is dan $T$ als $T^{prime}=6$ en $K=3$? Dan geldt: {T^{\prime}} = {K T} \Dus $6=3T$ en $T=2$.
Nu kijken we wat er gebeurt op de terugreis van Brigitta. Wat is $T^{\prime}$? We hebben $T^{\prime}=6$, $K=1/3$ en ^begin{equation} {T^{\prime}} = {K T^{\prime}}, ^quad (29) ^eind{equation} dus $6=T^{\prime}/3$ en $T^{\prime}=18$. De totale tijd gemeten door Albertina is dus $T+T^{\prime}=20$ jaar, dus zij is 20 jaar ouder als ze elkaar ontmoeten, terwijl Brigitta maar 12 jaar ouder is! Dus Albertina is 8 jaar ouder geworden dan Brigitta! Heb je het goed geraden? ????
Wat je zelf kunt proberen is wat experimenten met getallen. Je kunt je bijvoorbeeld voorstellen dat Brigitta een reis van bijvoorbeeld $10+10=20$ jaar maakt, en je kunt uitrekenen hoe snel ze moet reizen wil Albertina slechts één jaar ouder zijn geworden dan zij (d.w.z. er is $21$ jaar verstreken op Albertina’s klok) als Brigitta terugkomt. Misschien kunt u uitzoeken of het mogelijk is een realistische (d.w.z. haalbare) ruimtereis te maken waarbij tweelingen merkbaar ouder worden! Waarom wordt dit alles nu een paradox genoemd? Weet u nog wat paradox betekent ? We hebben eerder gezegd dat als twee mensen met constante snelheid bewegen (en dus constante snelheid ten opzichte van elkaar), veel van wat er gebeurt hetzelfde is, of we de eerste nu als stilstaand beschouwen en de tweede als bewegend, of andersom. Als we dat argument toepassen op Albertina en Brigitta, waarom kunnen we Brigitta in haar ruimteschip dan niet beschouwen als de persoon die stilzit, en Albertina op Aarde die wegvaart en dan terugkomt. Zo gezegd, klinkt het nogal dwaas, maar ik hoop dat je het idee begrijpt. Dan zouden we verwachten dat Brigitta ouder is dan Albertina als ze elkaar eindelijk ontmoeten. Maar we hebben al gezegd dat Albertina dan ouder is. Hoe kunnen beide beweringen waar zijn? Dat is de paradox! Zie je wat er mis is? Het punt is dat Brigitta zich niet tijdens haar hele reis met constante snelheid verplaatst ten opzichte van Albertina; ze heeft twee lange stukken van de reis waarin ze dat doet, maar daartussen is er een mogelijk kort maar zeer belangrijk stuk waar ze vertraagt, stopt en dan versnelt in de tegenovergestelde richting. Versnelling is een echt verschijnsel, zoals u waarschijnlijk weet van de attracties die u op een kermis misselijk maken! Weet u hoe dit met een eenvoudig apparaatje kan worden opgespoord?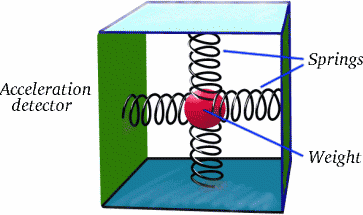
En wat vind je van dit alles? Het lijkt een beetje oneerlijk dat Brigitta mag reizen en meer van het heelal mag zien, maar uiteindelijk jonger is dan haar tweelingzus die thuisblijft – het leven lijkt niet altijd eerlijk! Maar het zou je moeten aanmoedigen om te reizen – niet noodzakelijk in de ruimte! – en avontuurlijk te zijn! Referentie Voor meer discussie over de tweelingparadox en de hier beschreven technieken kun je kijken naar het boek Flat and Curved Space-Times , van G.F.R. Ellis en mijzelf (uitgegeven door Oxford University Press in 1988). U zou ook de Mr. Tompkins boeken kunnen bekijken die de concepten van speciale relativiteit op een amusante en toegankelijke manier introduceren.

U kunt recensies vinden van de Mr. Tompkins boeken en ze bestellen op de Cambridge University Press website, bijvoorbeeld zie The New World of Mr. Tompkins : George Gamow’s Classic Mr. Tompkinsin Paperback