どちらの双子が年上か?
はじめに
この企画を進めていくと、驚くべき結論に導かれます! 一卵性双生児の片方が宇宙へ旅に出て、帰ってきて、地球の同じ場所に残っているもう片方の双子と自分(仮に彼女)の年齢を比べたとします。 その結果、一卵性双生児の片方は姉より年下であることが判明しました。 このプロジェクトの目的は、その方法を示すことです。
まず、推測ゲームから始めましょう。 旅をしている双子が、6年出て6年戻るという12年の旅に出たとします。 当然、帰ってきたときには12歳年をとっているはずです。 あなたがしなければならないのは、旅をしていない双子の年齢がいくつになるかを当てることです……! 移動する双子の速度は光速の5分の4とします。しかし、これはあなたの推測にあまり役立たないでしょう。 1から30の間の整数を当てることを提案しよう!
双子のことを考える前に、何が起こっているかを理解するために必要なある種の道具を用意する必要がある。 時空間図と呼ばれるある種のグラフを多用することになります。 グラフを使ったことがなくても心配しないでください。
?
グラフ
最も単純なグラフは、選んだ平面で何が起こっているかを描いたものです。 テーブルや机に座り、2本の定規と1枚の大きな紙を持っていると仮定しましょう。 左下の角から、定規を下に1つ、左上に1つ置き、その間に紙を挟み込みます。
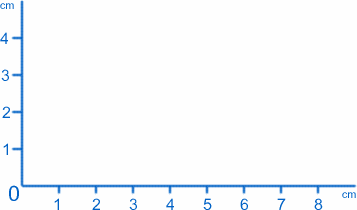
2つの定規が交わる点 (両方の目盛りでゼロ) を原点、略して O と呼び、定規を2つの軸にします。 慣例に従って、下にあるものを x 軸、横にあるものを y 軸と呼ぶことにします。 例えば、原点は $x=0$, $y=0$ である。 y軸から1cm$、x軸から2cm$の点は、$x=1$, $y=2$です(本当にこの通りなんです!)。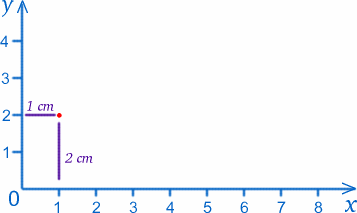
練習問題 自分でグラフを描き、次の点に印をつけましょう:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
それらはどんな形になるか
今度はとても汚い足のアリを想像してみましょう。 1匹は常にx軸から$1cm$の距離を保ちながら紙の上を歩いているとします。 その経路は直線となり、$y=1$という方程式で記述されます(前の文章で述べたことを言葉で表現したものです)。 別のものは、y 軸から常に $3cm$ 離れて歩くかもしれない。その経路の方程式は $x=3$ となる。 もっと独創的なアリは、両軸からの距離が常に同じになるように歩くかもしれません。 $x=1$, $y=1$; $x=2$, $y=2$; などを通り、その経路は $x=y$ という方程式で与えられます。 軸は相変わらず2本で、$x$と書かれた軸はある方向の距離を表しています。 例えば、O から 3cm$ 離れたところにボールがあるとする。そのボールの時空での経路は直線 $x=3$ となる。 例えば、$x=5$, $t=4$ は、ボールが原点から $4$ 秒後に $5cm$ のところにあることに対応します。
練習問題 ボールの歴史における次の出来事に対応する点をグラフ上にプロットしてください: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. 7199>次に、$x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$を考えてみましょう。 これらの点について、何か気がつくことがありますか? 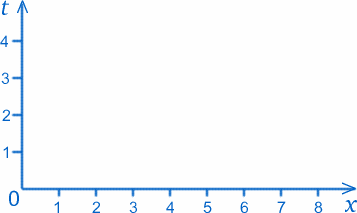
グラフ上でボールの軌道が直線であれば、ボールが一定の速度(おそらく速度ゼロ)で動いていることを意味します。 この場合、ボールが1秒間にどれだけの距離を移動したかを見ることで、速度を計算できます。x値の変化を対応するt値の変化で割るのです。 つまり、2つ目の例題では、ボールの速さは $2cm/sec$ となります。
練習問題 2点間を一定の速度で往復する(もちろん周期的に方向を変える)ボールの運動を表すグラフを描きましょう。 双子や宇宙旅行を考える上で面白いのは、特殊相対性理論と呼ばれる理論で、しばしば光線をグラフに描くことが必要です。 今、光線は何もない空間を一定の非常に大きな速度(ただし有限)で進んでいます。太陽から届く光線は約$8$分前にそこを出発しています(昔は光は無限に速く進むので、星を見た瞬間に見えると信じられていましたが、今では間違いであることが分かっています)。 正確には、光の速度は約300000000cm/sec$です。 これでは時空間グラフの軸がおかしなことになってしまうので、ここでは距離の測り方を変えてみることにする。 (t$の尺度が年であれば、対応するx尺度は光年となる)。 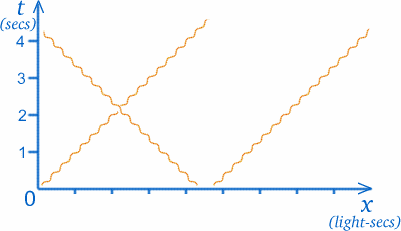
これの大きな利点は、光線の経路が軸に対して常に$45$度であることです。 つまり、Oを通る光線は、図にあるように、両軸に対して等しい角度を持つことになります。 (光は一定の速度で進むのでその経路は直線ですが、光線と質量を持つ他の物体の経路を区別するために、図のようにくねくねした線で表します。)
?
時間の測定
人々が今何時かについて意見が違うとき、誰かの時計が間違っているか、人々が異なるタイムゾーンにいるかだと思いがちです!しかし、それは間違いです。 しかし、それはもっと複雑なのです! 残念ながら、友人とチームを組んでこの理論を試してみても、理論が間違っているからではなく、あなたが走れるような速度では、たとえ超アスリートであっても、効果が小さすぎて観察できないため、がっかりすることでしょう。 この奇妙な現象が観察されるのは、速度が非常に大きくなったとき(光速の何分の一か)だけで、それも極めて正確な時計を使った場合だけです。
これがどのように機能するかを見るために、アインシュタインが提案したものと同様の「思考実験」を考えてみましょう。 (これは、実際に行うことができないので、「思考」実験であることはおわかりいただけるだろう)。 非常に強力な望遠鏡でビッグベンの時計を見ながら、そこから非常に速い列車で遠ざかり、ちょうど正午にその時計を通り過ぎたとしよう(列車がビッグベンのすぐ前を通ることはないことは知っているが、そのふりをしてみよう!)。 さて、もし列車が光速で移動できたとしたら、時計の針はどうなるのでしょうか? 12$を指したまま止まっているように見えるでしょう。 なぜか? それは、真昼に針が発した(あるいは針に反射した)光は、列車に乗っているあなたと全く同じ速度で時計から遠ざかり、それ以降の時間に発した光は列車に追いつくことができないからなのです! 奇妙だ!
これがなぜ「思考実験」なのかわかりますか(列車がビッグベンを通り過ぎないという事実とは全く別に)? それは、列車が実際には光速で動くことができないからです(これは特殊相対性理論が教えてくれる別のことですが、重さのある物体は決して光と同じ速さで動くことはできないのです)。 しかし、列車が光速の半分の速さで動いたとしたら(それでも非常に速い)、時計の針は動くが、あなたの時計の針よりゆっくり動くのがわかるだろう 時間の計測は、自分がどのように動いているかに依存するのです!
どうしてそうなるのでしょうか? これを理解するために、特殊な時計、光時計について考えてみましょう。 このような時計がベッドの横に置いてあって、朝、あなたを目覚めさせることはないでしょう。 この時計は、光源が信号を発し、それが距離Dを移動して光源に反射される仕組みになっています。 信号が送信され、それが受信されて戻ってくるまでの時間差または間隔が、時計の目盛りを定義しています。 \但し、$c$は光速を表す。 (速度=距離/時間なので、時間=距離/速度であることを忘れずに。)
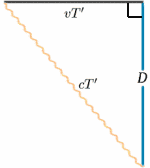
さて、動いているロケットがこのような時計を搭載しているとしよう–乗員の経験では、刻みは $2T$ の間隔で発生すると思うだろう。 ここで、静止しているロケットの乗組員が、動いているロケットの時計を観察し、自分たちの時計と比較すると、やはり2T$の間隔で時を刻んでいる。 何が見えるでしょうか? 下の図から答えがわかると思います。 (5939>
動いているロケットは、信号を送ってから反射して戻ってくるまでの中間の時間で鏡に光が反射していることがわかります。 静止しているロケットからは、移動時間が $2T^{ \prime}$ と言っているように見える。 これはピタゴラスの定理を使って計算できます。
 |
 |
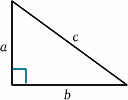
{a^2 + b^2} = {c^2} とします。 ロケットの図では、直角三角形があるので、♪begin{equation}となります。 D^2 + v^2 T^{‘2} = {c^2 T ^{prime 2}}}quad (2) \end{equation} 次に、これを $T^{prime}$ について解きます。 \⑯{begin{equation} {T^{} (c^2 – v^2)} = {D^2}, ⑯{equation} (3) ⑭{end{equation} $T^{prime}$を解きます。 \ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ {c \sqrt{(1 – v^2/{c^2})}}}quad (5) \end{equation} and so \begin{equation} {T^{prime}} = {frac {T} {sqrt{(1 – v^2/{c^2})}}, \quad (6) \end{equation} and clock rates will be different from the different (unless of course $v=0$). 実際、$T^{prime}$は$T$より大きいので、静止しているクルーには動いている時計の方が刻みの間隔が長く、ゆっくり進んでいるように見えます。
万人に通用する時間の定義がないことを認めたら、時間を測ることの本当の意味を考えなければなりません。 ある意味で、私たちは時空間の経路に沿った距離を測定しています(時空間図に戻って考えてみてください)。 双子は時空の中で異なる経路をたどっているので、彼らが経験した時間は異なってもそれほど不思議ではありません。 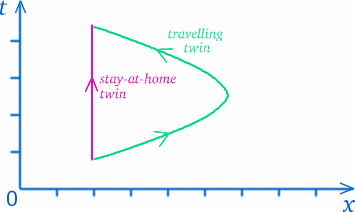
しかし、結論を急ぐな!物事は常に見かけ通りとは限らないのだ…。 旅をしている双子の道は長く見えますが、それは彼女がより多くの時間を経験したということでしょうか? この種の問題がいかに厄介であるかを理解するために、似たような状況を考えてみましょう。 例えば,あなたがケンブリッジの南側にあるトランピントンに住んでいて,市の中心部の北側にあるテスコに買い物に行きたいとする(できるだけ,歩行者天国を避けて). 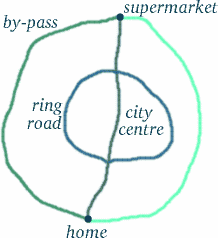
一日のほとんどの時間帯で、最も長いルートであるバイパスに最も時間がかかり、次にリングロードが続くことがわかります。
ここまで、光信号を使って時間を計測する方法について見てきました。 正確な時計があれば、遠くの物体から反射してくる光やレーダーの信号を使って距離を測ることができます。距離は光の移動時間の半分に光速を掛けたものになります。
K-factors
これから、今までお話ししたような効果の計算をするのに役立つ考え方を説明します。
宇宙飛行士B(ベンの場合)がロケットに乗って、宇宙ステーションにいる別の宇宙飛行士A(アルフの場合)から速度 $c/5$ で離れているとします。 年に一度、3月13日にアルフはベンに誕生日の挨拶を送る。 2010年のこの挨拶を伝える無線メッセージは、宇宙ステーションで測定したところ、 半光年の距離を移動してロケットに到達し、その間に半年がかかったとする。 次のメッセージはちょうど1年後に送信されます。 この信号が、ベン宇宙飛行士が前の信号を受信した場所まで半年間移動したとき、ロケットは5分の1光年先に移動しているので、この信号はロケットに追いつくためにもっと長い距離を移動しなければなりません。 哀れなアルフは、アルフの時計によれば、毎年送る誕生日の挨拶は、1年4分の1の間隔でベンに届くと結論付けている。 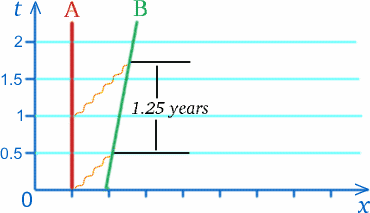
これは、Benがこの間隔をどう測定するかはわかりませんが、1年でない可能性があることは示唆されています! 同様の効果はベンからアルフに送られる信号にも起こります。
さて、一般的なケースを見て、これをより正確にしましょう。 2人の観測者アルフとベンが一定の速度で互いに遠ざかると考える。 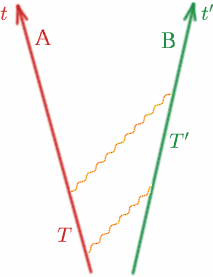
アルフは光信号を送り、さらに時間$T$後に別の信号を送る。 ベンは自分の時計にしたがって、2つの信号を時間$T^{prime}$の差で受信する。 そこで、量$K$を次のように定義する。 \begin{equation} {K} = {T^{Θprime}/T}。 なお、アルフとベンが同じ速度で(同じ方向に!)移動していれば、$K$は1である。 K$ がアルフとベンの相対速度にどのように依存するかは、もう少し詳しく見てみましょう。 K$ はドップラーシフト係数と呼ばれることもあり、その効果は音波のそれと似ています。救急車やパトカーのサイレンが近づいたり遠ざかったりするときの音の変化は皆さんご存知でしょう。 明らかに、観測者が光信号の送受信を記録しておき、後で会ったときに$T$と$T^{prime}$、ひいては$K$を計算できるようにすることである。 もう一つの可能性は、一方が非常に強力な望遠鏡を持っていて、もう一方の時計を見ることである(これはまさにビッグベンを通過する列車の再来だ!)
この数$K$について、私たちに役立つようにいくつかの仮定をしておく必要がある。 まず、アルフとベンが一定の速度で動いているとき、$K$は$T$と$T^{prime}$をいつ測ったかによらず、$T$の大きさにもよらないことを仮定します。 ですから、例えばアルフが光信号を送るまでの時間を2倍にしても、$K$は同じになります。 この場合の数字$T_1^{prime}$, $T_2^{prime}$, $T_3^{prime}$ を埋めてみてください。
?
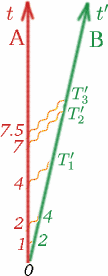
(なお、時間の計測を始めるのは2人の観測者が揃ったときで、その時点でストップウォッチをゼロにしておけばOKです。) ですから、一般的には
?
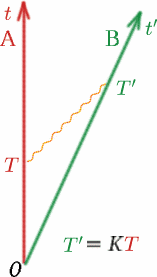
第二に、これも同様に重要ですが、ベンがアルフからの光信号に対して測定した$K$は、アルフがベンからの光信号に対して測定したものと同じであると仮定しています。 なぜこのように仮定するのでしょうか。 道路で2台の同じ車が背中合わせに走っていると想像してください。 車$A$は静止し、車$B$は$A$から時速$50kmで遠ざかっていく。 A$の後ろの窓から見ている乗客は、$B$が適切な速度で消えていくのを見ることができる。 B$の乗客が自分の後ろの窓から見ると、非常によく似た絵が見える – 車$A$が同じ速度で遠ざかっていくように見えるのだ 列車に乗っていて、列車が走り去ったと思ったら、隣の列車が反対方向に走り去り、自分の列車は静止していた、というような不思議な経験をしたことはありませんか。
この仮定により、一方の観測者が他方に協力しなくても、レーダーで$K$を測定することができます。 どうすればいいか、わかる人はいますか? ヒントをあげましょう。
いつものように、アルフとベンが一定の速度で離れて移動しているとします。 アルフは2つの信号を$T$間隔で発信し、ベンは$T^{prime}$間隔でそれを反射し、アルフは$T^{prime}$間隔でそれを受信する。 アルフはどうやって$K$を計算するのか?
?
◇begin{equation} {T^{Cacheprime}} = {K T} ◇begin{equation} {T^{Cacheprime}} = {K T} ◇begin{equation} {T^{Cacheprime}} = {K T \(9)、(10)、(11)、(12)、(13)、(14)、(15) \begin{equation} {T^{Centa}} = {K T^{Centa}}quad (10) \end{equation}. したがって、 \begin{equation} {T^{Copyright} = {K(K T)} = {K^2 T}quad (11) \end{equation} ですから、 \begin{equation} {K} = {}sqrt{T^{Copyright}/T}} となります。 \(12) ⑭end{equation}となります。 問題 複雑なドッキング操作を行うには、2つの宇宙船が相対的に静止していることが不可欠である。
Kと速度の関係
アルフとベンの相対速度が0であれば、$K$ = $1$ であることは既に知っている。 一般的な速度の場合、その値はどうなるのでしょうか。 これを計算するには、先ほどの考え方に加えて、同時性の考え方を利用した賢い方法があります。 どういうことでしょうか?
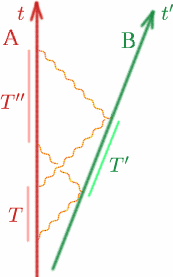
まず、いつもの2つの観測者が一定の速度 $v$ で遠ざかる様子を想像してみましょう。 二人が一緒にいるとき、二人とも時計を $t = 0$ に合わせたとしましょう。 アルフの時計で時刻 $T$ にアルフが電波を発信し、ベンの時計で時刻 $T’$ に反射し、アルフの時計で時刻 $T^{prime\prime}$ に再び反射してきたとする。 例によって絵を描いてみましょう。
?
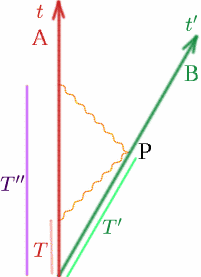
今、 \begin{equation} {T^{cacheprime}} = {K T}quad (13) \end{equation} が分かりました。 \begin{equation} {T^{Cheat}} = {K T^{Cheat}} = {K^2 T}. \⑭⑯⑯⑯エンド そこで、アルフは、電波パルスの移動時間は♪{begin{equation} {T^{Prime}-T} = {K^2 T-T} = {(K^2-1)T}, ♪{quad (15) ♪end{equation} と考え、自分とベンとの距離$D$は電波の伝わる距離の半分、つまり速度の半分×時間である、と計算する。 \⑭D= {frac {1} {2} c(K^2-1)T} となります。 さて、アルフとベンの距離は常に変化していることがわかったので、「これがいつ(つまり何時)アルフとベンの距離になるのか」を考える必要があります。 ここで、同時性という考え方が必要になります。 ベンが点 $P$ にいるときに距離が測定されるのは明らかですが、これがアルフにとって何時に相当するのでしょうか。 さて、アルフは電波パルスの往復距離が同じであることを知っているので、アルフが$P$と同時と判断した事象$Q$は、$T$と$T^{prime\ prime}$の中間に位置することになります。 (アルフにとって$Q$は$P$と同時であると言いますが、それは単に同時という意味です)。 ということは、$Q$の時刻は \begin{equation} {T_Q} = {}frac {1} となります。 {2}(T+T”)} = {frac {1} (T+T”) {2} (K^2+1)T}とする。 したがって、アルフは、ベンが時間$T_Q$の間に距離$D$を移動したと結論付けるので、彼の速度$v$は、以下のように与えられる: \begin{equation} {v} = {frac {D} }. {T_Q}} = {{frac {1}} {2} c(K^2-1)T} {frac {1}{2} (K^2+1)T}}となる。 したがって、{begin{equation}} {frac {v} {c}} = {frac {K^2-1} {K^2+1}} が得られます。 \(19) ⑭end{equation}となります。 ここで、$K$を$frac {v} {c}$の項で計算することができる。 \(K^2+1)\frac {v} {c}} = {K^2-1}, \begin{equation} { (20) ⑭end{equation} で計算できます。 \ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ。 + \frac{v}{c}} = {K^2-1}, \end{equation} (21)⑷. \Ȃ{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation}. 従って、ⅳbegin{equation} {K^2} = {{frac {1+ \frac{v}{c}}}} となる。 {1- \frac{v}{c}}}quad (23) \end{equation} よって、 \begin{equation} {K} = \sqrt{{left({}frac{1+|prefrac{v}}{1-|prefrac{v}}}right)}} となる。 \Ȃ (24) Ȃエンド{equation}となります。
例えば $v = c/4$ とすると $K = \sqrt{5/3} = 1.291$ となります。
今度は $v = c/2, 9c/10, 99c/100$ としてみましょう。
ここで、アルフとベンが動いていてもいなくても、$K$は変わりません。
例えば、アルフとベンが相対速度$c/2$で接近している場合、
同じ式が使えます。 K = \sqrt{{left({}frac{1+(-1/2)}{1-(-1/2)}}}right)}} = \sqrt{{left({}frac{1/2}{3/2}}right)}} = \sqrt{1/3}. \(25) ⑭エンド{式}.
1)時速1000kmで接近する旅客機$;
2)時速500kmで離れていく銀河団$;
3)時速100kmで警官に近づく車$;
4)時速5kmで友人に向かって歩くあなた$これらの効果の中で観測できるものがありますか? 双子のパラドックス – ついに!
何が起こるのでしょうか? なぜパラドックスなのでしょうか? (パラドックスという言葉の意味は?)
一卵性双生児のアルベルティーナとブリギッタを考えてみましょう!
アルベルティーナとブリギッタは、一卵性双生児です。 アルベルティーナはロンドンの家にいて、冒険好きなブリギッタは宇宙旅行に行きます。 彼女は、$v = 4c/5$で航行する非常に速い宇宙船に乗って、時計で測ると6年間地球から離れたところにいる。 その後、同じ速度で6年かけて戻ってくる。 つまり、ブリギッタがロンドンのアルベルティーナのもとに戻ったとき、彼女は12歳年をとっている。 でも、アルベルティーナは何歳年上なのでしょうか? あなたの推測が正しかったのか、それとももう少しだったのか、見てみましょう!
時空図を書いてみましょう。 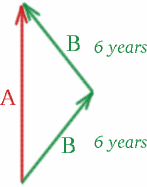
ブリギッタの往路では、双子は相対速度$v = 4c/5$で離れていくので、 \begin{equation} {K^2} = {}frac{1+frac{4}}{1-frac{4}} = {9}, \quad (26) \end{equation} となり$K=3$となります。 Brigittaの帰り道、2人は同じ速さで接近するので、 \begin{equation} {K^2} = {{1-frac{4}}{1+frac{4}}}quad (27) \end{equation} となり$K=1/3$となります。 あとは、信号機を1台入れるだけで、アルベルティーナが計測する時間を計算することができます。 7199>アルベルティーナが、ブリギッタがちょうど振り向こうとする地点$U$に届くように選んだ点$S$で信号を送ったとする。 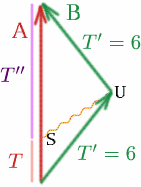
では、$T^{prime}=6$、$K=3$のとき、$T$は何でしょうか。 ここで、{T^{prime}}={K T}となります。 \quad (28) \end{equation}
だから $6=3T$ と $T=2$。
今度は Brigitta の帰路で何が起こるか見てみましょう。 T^{prime}$ は何でしょうか。 T^{prime}=6$, $K=1/3$ で、 \begin{equation} {T^{}} = {K T^{}}, \quad (29) \end{equation} なので $6=T^{prime}/3$, $T^{prime}=18$ となります。 したがって、アルベルティーナが測った時間の合計は$T+T^{Θprime}=20$年なので、出会った時点で20歳年上なのに対し、ブリギッタは12歳年上でしかない!? つまり、アルベルティーナはブリギッタより8歳多く年をとっているのです!
では、正解でしたか?
自分でできることとしては、数字を使った実験がありますね。 例えば、ブリギッタが10+10=20$年の旅をしたと想像して、ブリギッタが戻ってきたときに、アルベルティーナが自分より1年だけ年をとっている(つまり、アルベルティーナの時計では21$年経過している)ためには、どのくらいの速さで旅をしなければならないかを計算することができる。 おそらく、双子の年齢が顕著に異なるような現実的な(つまり達成可能な)宇宙旅行が可能かどうか調べられるでしょう!
さて、なぜこのようなことがパラドックスと呼ばれているのでしょうか? パラドックスとはどういう意味か覚えていますか? 先ほど、2人の人間が一定の速度で動いている場合(つまり、お互いの相対速度が一定の場合)、1人目が静止していて2人目が動いていると考えても、その逆でも、起こることの多くは同じである、と述べました。 この議論をアルベルティーナとブリギッタに当てはめると、宇宙船に乗ったブリギッタはじっとしている人、地球にいるアルベルティーナは出航して戻ってくる人と考えることができるのではないでしょうか。 というと、かなりバカバカしいですが、お分かりいただけるでしょうか。 そうすると、ブリギッタはアルベルティーナより年上で、やっと会えたということになる。 しかし、その時はすでにアルベルティーナの方が年上だと言っているのです。 どうして両方が正しいのでしょうか? これはパラドックスです!
何が間違っているかわかりますか?
ポイントは、ブリギッタは全行程でアルベルティーナに対して一定の速度で動いているわけではないことです。 これが、すべての違いを生むのです!加速は、お祭りで気分が悪くなる乗り物を見ればわかるように、実際にある現象なのです。 加速度を簡単な装置で検出する方法をご存知ですか? 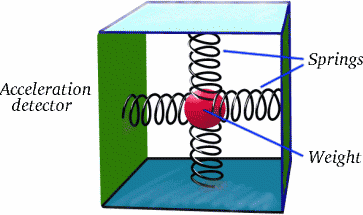
では、これらのことをどう考えるか? ブリギッタが旅行して宇宙をもっと見ることができるのに、家に閉じこもっている双子の妹より若いというのは、ちょっと不公平な気がします。 しかし、これは、必ずしも宇宙を旅する必要はないのです。 – と冒険心をくすぐられるはずです。 参考文献 双子のパラドックスとここで述べた手法については、G. F. R. Ellisと私による「Flat and Curved Space-Times 」(1988年にオックスフォード大学出版局から出版)という本を見てみるとよいでしょう。 また、特殊相対性理論の概念を面白くて親しみやすい方法で紹介しているトンプキンス氏の本も見てみるとよいでしょう。
トンプキンス氏の本のレビューを見たり、ケンブリッジ大学出版局のホームページから注文できます。