Introduzione

Se seguirai questo progetto, sarai portato ad una conclusione sorprendente! Supponiamo che uno di una coppia di gemelli identici faccia un viaggio nello spazio e poi ritorni per confrontare la sua (diciamo la sua) età con quella dell’altro gemello che è rimasto nella stessa posizione sulla Terra. Si scopre che dopo il viaggio, un gemello sarà più giovane di sua sorella! Ti starai chiedendo come ciò sia possibile, e lo scopo di questo progetto è di mostrarti come.
Iniziamo con un gioco di indovinelli – scopriremo se hai ragione alla fine! Supponiamo che la gemella viaggiatrice faccia un viaggio di 12 anni – 6 anni fuori e 6 anni indietro. Ovviamente avrà 12 anni in più quando tornerà. Quello che devi fare è indovinare quanto più vecchio sarà il gemello non viaggiatore….! Ho bisogno di dirvi a che velocità viaggia il gemello in movimento – diciamo quattro quinti della velocità della luce – anche se oserei dire che questo non vi aiuterà molto nella vostra ipotesi! Vi suggerisco di indovinare un numero intero tra 1 e 30!
Prima di considerare i gemelli, dobbiamo predisporre alcuni strumenti di cui avremo bisogno per capire cosa sta succedendo. Faremo molto uso di un certo tipo di grafico chiamato diagramma spazio-temporale. Non preoccupatevi se non avete mai usato i grafici prima – cercheremo di iniziare dalle basi.
?

Grafi

Il tipo più semplice di grafico è solo un’immagine di ciò che sta succedendo su una superficie piana scelta. Supponiamo che tu sia seduto a un tavolo o a una scrivania, e che tu abbia due righelli e un grande pezzo di carta. Partendo dall’angolo in basso a sinistra, mettete un righello lungo il fondo e uno sul lato sinistro, con la carta in posizione tra loro. Quello che hai dovrebbe assomigliare a questo:

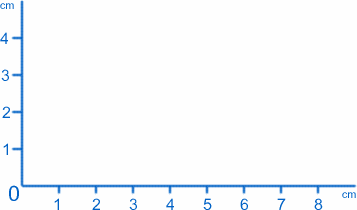
Chiameremo il punto in cui i due righelli si incontrano (lo zero su entrambe le scale) l’origine, o O in breve, e i righelli forniscono i due assi. Seguendo la convenzione, chiameremo l’asse x lungo il fondo e l’asse y lungo il lato. Possiamo etichettare qualsiasi punto della carta con i suoi valori di $x$ e $y$: per esempio, l’origine ha $x=0$, $y=0$. Il punto a $1cm$ dall’asse delle y e $2cm$ dall’asse delle x ha $x=1$, $y=2$ (ho davvero capito bene!).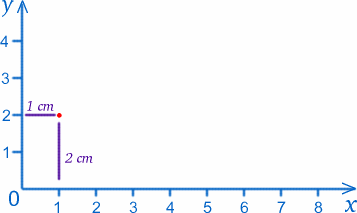

Esercitazione Disegna il tuo grafico e segna i seguenti punti:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Che forma hanno? Supponiamo che una cammini sulla carta rimanendo sempre ad una distanza di $1cm$ dall’asse x. Il suo percorso sarebbe una linea, descritta dall’equazione $y=1$ (un modo elegante per dire ciò che è detto a parole nella frase precedente). Un’altra potrebbe camminare sempre a $3cm$ dall’asse y; l’equazione del suo percorso sarebbe $x=3$. Una formica un po’ più originale potrebbe camminare in modo che la sua distanza da entrambi gli assi sia sempre la stessa; passerebbe per $x=1$, $y=1$; $x=2$, $y=2$; ecc e il suo percorso sarebbe dato dall’equazione $x=y$.

Diagrammi spazio-temporali

In questa sezione, disegneremo alcuni grafici che sembrano molto simili a quelli della sezione precedente, ma il loro significato sarà piuttosto diverso. Abbiamo ancora due assi, e quello etichettato $x$ rappresenta ancora la distanza in una certa direzione. Tuttavia quello che era etichettato $y$ è ora etichettato $t$, che rappresenta il tempo, misurato in secondi diciamo.Immaginate per esempio una palla in un punto fisso a $3cm$ da O; il suo percorso nello spazio-tempo sarà la linea retta $x=3$. Ora supponiamo che la pallina rotoli lungo un percorso rettilineo; allora i punti sul grafico corrisponderebbero alle posizioni della pallina in momenti particolari, per esempio $x=5$, $t=4$ corrisponderebbe alla pallina che si trova a $5cm$ dall’origine $4$ secondi dopo l’inizio della misurazione del tempo.
Esercizio Traccia i punti sul grafico corrispondenti ai seguenti eventi nella storia della pallina: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Come lo interpreteresti?
Prova ora con $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Cosa notate su questi punti?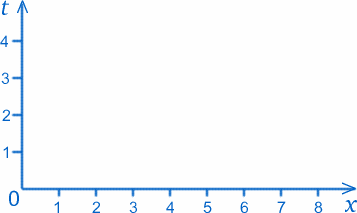
Se il percorso della palla è una linea retta sul grafico, significa che la palla si sta muovendo con velocità costante (forse velocità zero). In questo caso possiamo calcolare la velocità vedendo quanto viaggia la palla in un secondo – dividiamo il cambiamento del valore di x per il corrispondente cambiamento del valore di t. Quindi, nel nostro secondo esempio, la velocità della palla è $2cm/sec$. Sei d’accordo?
Esercizio Disegna un grafico che rappresenti il moto di una palla che si muove avanti e indietro tra due punti, con velocità costante (ma cambiando periodicamente direzione, ovviamente).
Ora faremo qualcosa di piuttosto strano al nostro grafico. Nella teoria chiamata relatività speciale, che è ciò che rende interessante pensare ai gemelli e ai viaggi nello spazio, abbiamo spesso bisogno di tracciare i raggi di luce sui nostri grafici. Ora i raggi di luce viaggiano nello spazio vuoto con una velocità costante e molto grande (ma finita); un raggio di luce che vi raggiunge dal sole è partito da lì circa $8$ minuti fa (un tempo si credeva che la luce viaggiasse infinitamente veloce in modo da poter vedere le stelle nel momento in cui le si osservava, ma ora si sa che questo è sbagliato). Per essere più precisi, la velocità della luce è di circa $30000000000cm/sec$! Questo potrebbe portare a delle scale molto strane sugli assi di un grafico dello spazio-tempo, quindi sceglieremo di misurare la distanza in modo diverso; le unità sull’asse x saranno i secondi-luce, cioè la distanza percorsa dalla luce in un secondo. (Se la scala per $t$ è anni, la corrispondente scala x sarà anni luce).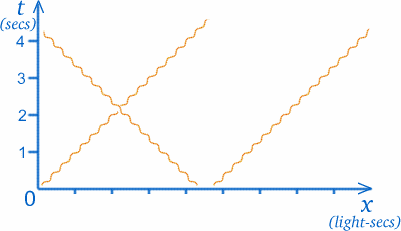
Il grande vantaggio di questo è che il percorso di un raggio di luce sarà sempre a $45$ gradi rispetto agli assi. Questo significa che un raggio di luce attraverso O sarà ad angoli uguali per entrambi gli assi, come si vede nel diagramma. (Anche se la luce viaggia a velocità costante, quindi il suo percorso è una linea retta, la rappresentiamo con una linea ondulata, come mostrato, per distinguere i raggi di luce dai percorsi di altri oggetti con massa.)
?

Misurare il tempo

Tendiamo a supporre che quando le persone non sono d’accordo su che ora sia, l’orologio di qualcuno è sbagliato, o forse le persone sono in fusi orari diversi! Ma è ancora più complicato di così! Secondo la relatività speciale, due persone possono trovarsi nello stesso posto e correlare i loro orologi, ma se uno si muove rispetto all’altro, in seguito non saranno d’accordo su che ora è. Sfortunatamente se fai squadra con un amico e provi a testare questa teoria, rimarrai deluso, non perché la teoria sia sbagliata, ma perché alla velocità a cui probabilmente sarai in grado di correre, anche se sei un super-atleta, l’effetto sarà troppo piccolo da osservare. È solo quando le velocità diventano molto grandi (frazioni considerevoli della velocità della luce) che questo strano fenomeno può essere osservato e, anche allora, solo utilizzando orologi estremamente precisi.
Per vedere come questo potrebbe funzionare, consideriamo un “esperimento del pensiero” simile a quello suggerito da Einstein. (Si tratta di un esperimento “pensato” piuttosto che reale perché non può essere fatto realmente, come vi renderete conto). Supponete di guardare l’orologio del Big Ben attraverso un telescopio molto potente, mentre vi allontanate da esso su un treno molto veloce che passa davanti all’orologio esattamente a mezzogiorno (so che i treni non passano davanti al Big Ben, ma facciamo finta!) Ora, se il treno potesse muoversi alla velocità della luce, cosa vedresti accadere alle lancette dell’orologio? Sembrerebbero ferme, entrambe rivolte a $12$! Perché? Perché la luce emessa (o riflessa) dalle lancette a mezzogiorno si allontanerebbe dall’orologio esattamente alla stessa velocità con cui ti muovi tu sul treno, e la luce emessa in momenti successivi non potrebbe raggiungere il treno! Strano!
Capisci perché questo è un “esperimento di pensiero” (a parte il fatto che i treni non passano davanti al Big Ben)? È perché un treno non potrebbe effettivamente muoversi con la velocità della luce (che è un’altra cosa che ci dice la relatività speciale – qualsiasi oggetto che pesa qualcosa non può mai muoversi alla stessa velocità della luce). Ma supponiamo che il treno si muova a metà della velocità della luce (ancora molto veloce) – vedresti le lancette dell’orologio muoversi, ma più lentamente di quelle del tuo orologio! La misurazione del tempo dipende da come ci si muove!
Come può essere? Per capirlo, consideriamo un tipo speciale di orologio, un orologio leggero. Non è probabile che ne troviate uno accanto al vostro letto che vi sveglia al mattino. Consiste in una fonte di luce che emette segnali che viaggiano per una distanza D e vengono poi riflessi alla fonte. L’intervallo di tempo tra ogni volta che un segnale viene emesso e quando viene ricevuto indietro, definisce i ticchettii dell’orologio; essi si verificano a distanza di $2T$, dove \inizio{equazione} {T} = {D/c} \con $c$ che rappresenta la velocità della luce. (Ricorda che la velocità = distanza/tempo, quindi il tempo = distanza/velocità.)

Ora supponiamo che un razzo in movimento abbia un tale orologio – l’esperienza dell’equipaggio sarà che i ticchettii avvengono ad intervalli di $2T$. Ora supponiamo che l’equipaggio di un razzo fermo osservi l’orologio del razzo in movimento e lo confronti con il proprio, anch’esso con un ticchettio a intervalli di $2T$. Cosa vedranno? I diagrammi qui sotto dovrebbero suggerire la risposta. (Mi dispiace che i miei razzi assomiglino di più a dei pesci!)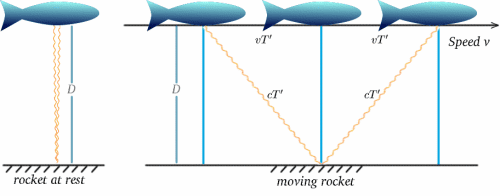
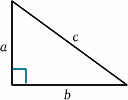
Per il razzo in movimento, la luce viene riflessa dallo specchio a metà strada tra quando il segnale viene inviato e quando viene riflesso. Dal razzo fermo, il tempo di viaggio sembra essere $2T^{ \primo}$ diciamo. Possiamo risolvere questo problema usando un teorema molto importante (un nome di fantasia per qualcosa che è stato dimostrato essere vero in matematica!) – quello di Pitagora.

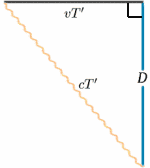{begin{equazione} {a^2 + b^2} = {c^2} \quadro (1) \fine equazione} Nel diagramma del razzo, abbiamo un triangolo rettangolo, quindi \begin{equazione} D^2 + v^2 T^{‘2} = {c^2 T ^{primo 2} \quadro (2) \end{equazione} Ora risolviamo questo per $T^primo}$: \T^primo 2} (c^2 – v^2)} = {D^2}, \quadro (3) \fine equazione} \inizio equazione {T^{primo 2} c^2 (1 – v^2/{c^2})} = {D^2} \quadrato (4),\fine dell’equazione,\dando come risultato {T^T^primo} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})\quadro (5) \end{equazione} e così \begin{equazione} {T^{prime}} = {frac {T} {sqrt{ 1 – v^2/{c^2})\quadro (6) \end{equazione} e le velocità di clock saranno diverse (a meno che, naturalmente, $v=0$). Infatti $T^{primo}$ è più grande di $T$, quindi all’equipaggio fermo sembra che l’orologio in movimento abbia intervalli più lunghi tra i ticchettii e quindi stia andando lento.
Una volta accettato che non esiste una definizione universale di tempo che valga per tutti, dobbiamo pensare a cosa intendiamo veramente per misurare il tempo. In un certo senso, stiamo misurando le distanze lungo i nostri percorsi nello spazio-tempo (ripensiamo al diagramma spazio-tempo). I gemelli seguono percorsi diversi nello spazio-tempo, quindi non è così sorprendente che abbiano sperimentato quantità diverse di tempo.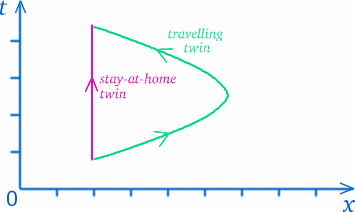
Ma non saltare alle conclusioni – le cose non sono sempre come sembrano…! Il percorso della gemella viaggiatrice sembra più lungo, ma questo significa che ha vissuto più tempo? Per vedere quanto sia complicato questo tipo di domanda, pensa a una situazione che potrebbe essere piuttosto simile. Supponiamo che tu viva a Trumpington, nella parte sud di Cambridge, e che tu voglia andare a fare la spesa da Tesco all’estremità nord del centro città (il più possibile, evitando le zone pedonali), sulla circonvallazione o sulla tangenziale – vedi il diagramma qui sotto.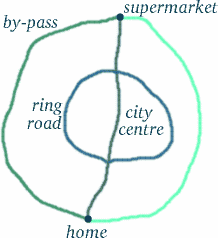
Nella maggior parte delle ore del giorno, troverà che il percorso più lungo – la tangenziale – richiede meno tempo, seguito dalla tangenziale. Ora sei convinto che la risposta più ovvia non è sempre quella giusta?
Abbiamo visto come si misura il tempo usando i segnali luminosi. Una volta che abbiamo un orologio accurato, possiamo misurare la distanza usando i segnali luminosi o radar riflessi dall’oggetto distante; la distanza sarà la metà del tempo di percorrenza della luce, moltiplicato per la velocità della luce.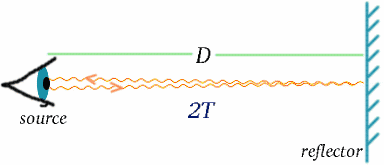

Equazione iniziale {D} = {cT}quadrato (7) \end{equazione} Come il tempo, la distanza è una quantità in cui il risultato della misura dipende dal modo in cui l’osservatore si sta muovendo.

Fattori K

Vi descrivo ora un’idea che dovrebbe aiutarci a fare calcoli del tipo di effetto di cui vi ho parlato.
Supponiamo che un astronauta B (per Ben) sia in un razzo che si muove a velocità $c/5$ lontano da un altro astronauta A (per Alf) in una stazione spaziale. Una volta all’anno, il 13 marzo, Alf manda gli auguri di compleanno a Ben. Supponiamo che il messaggio radio che porta questi auguri nell’anno 2010 sia misurato dalla stazione spaziale per percorrere una distanza di mezzo anno luce per raggiungere il razzo, impiegando mezzo anno per farlo. Il messaggio successivo viene inviato esattamente un anno dopo. Quando questo segnale radio ha viaggiato per mezzo anno fino al punto in cui l’astronauta ha ricevuto il segnale precedente, il razzo si è spostato un quinto di anno luce più avanti, quindi questo segnale deve viaggiare più a lungo per raggiungere il razzo; infatti, il tempo misurato da Alf quando il segnale raggiunge il razzo è tre quarti di un anno dopo che è stato inviato – vedi il diagramma sotto. Il povero Alf conclude che gli auguri di compleanno inviati ogni anno saranno ricevuti da Ben a intervalli di un anno e un quarto, secondo l’orologio di Alf.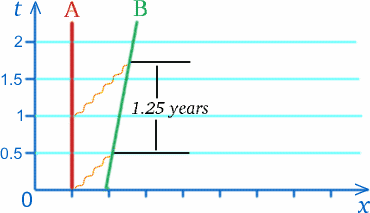
Questo non ci dice cosa misurerà Ben per questi intervalli, ma suggerisce che potrebbe benissimo non essere un anno! Un effetto simile avverrà per i segnali inviati da Ben ad Alf.
Ora guardiamo il caso generale e rendiamo questo più preciso. Consideriamo due osservatori Alf e Ben che si allontanano l’uno dall’altro a velocità costante.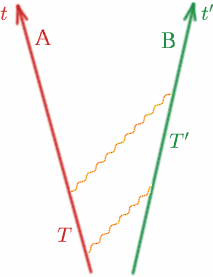
Alf invia un segnale luminoso e poi un altro al tempo $T$ successivo. Ben riceve i due segnali a distanza di $T^{primo}$, secondo il suo orologio. Allora definiamo una quantità $K$ con la seguente equazione: {K} = {T^{primo}/T}. \quadrato (8) \fine equazione} Si noti che se Alf e Ben si muovessero con la stessa velocità (nella stessa direzione!), $K$ sarebbe uno. Vedremo meglio come $K$ dipende dalla velocità relativa di Alf e Ben. $K$ è a volte chiamato fattore di spostamento Doppler e l’effetto è simile a quello delle onde sonore – dovete tutti conoscere il cambiamento di suono della sirena di un’ambulanza o di un’auto della polizia quando si avvicina e poi si allontana.
Come possiamo misurare $K$? Il modo più ovvio è che gli osservatori registrino quando i segnali luminosi vengono inviati e ricevuti in modo da poter calcolare $T$ e $T^{primo}$, e quindi $K$, quando si incontrano più tardi. Un’altra possibilità sarebbe che uno dei due abbia un telescopio molto potente con cui guardare l’orologio dell’altro (questo è davvero il treno che passa davanti al Big Ben di nuovo!).
Dobbiamo fare alcune ipotesi su questo numero $K$ perché ci sia utile. Assumiamo innanzitutto che quando Alf e Ben si muovono a velocità costante, allora $K$ non dipende da quando $T$ e $T^{primo}$ vengono misurati, né dipende da quanto è grande $T$. Quindi, per esempio, se Alf aspetta il doppio del tempo tra un segnale luminoso e l’altro, $K$ sarà lo stesso. Vedi se riesci a riempire i numeri $T_1^{primo}$, $T_2^{primo}$, $T_3^{primo}$ in questo caso.
?

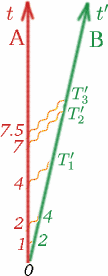
(Nota che va bene iniziare a misurare il tempo quando i due osservatori sono insieme, ed entrambi possono impostare i loro cronometri a zero in quel momento). Quindi in generale abbiamo
?

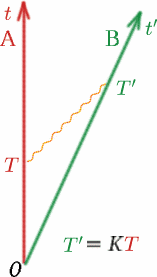
La seconda cosa che assumiamo, che è altrettanto importante, è che il $K$ misurato da Ben per i segnali di luce da Alf sia lo stesso di quello misurato da Alf per i segnali di luce da Ben. Perché assumiamo questo? Immaginate due auto identiche una dietro l’altra su una strada. L’auto $A$ rimane ferma e l’auto $B$ si allontana da $A$ a $50km/h$. I passeggeri che guardano dal finestrino posteriore di $A$ vedranno $B$ scomparire alla velocità appropriata. I passeggeri di $B$ vedranno un’immagine molto simile se guardano attraverso il loro finestrino posteriore – l’auto $A$ sembrerà allontanarsi alla stessa velocità! Avete mai avuto quella strana esperienza di essere seduti in un treno e pensare che si sia appena mosso, quando si scopre che era il treno vicino che si muoveva nella direzione opposta e il vostro treno era ancora fermo?
Questa assunzione rende possibile per un osservatore misurare $K$ con il radar senza alcuna cooperazione da parte dell’altro. Qualcuno può indovinare come? Lasciate che vi dia un indizio.
Supponiamo come al solito che Alf e Ben si stiano allontanando con velocità costante. Alf invia due segnali ad un intervallo di $T$, Ben li riflette ad un intervallo $T^{primo}$ e Alf li riceve di nuovo ad un intervallo $T^{primo\primo}$. Come può Alf calcolare $K$?
?

Rispondere

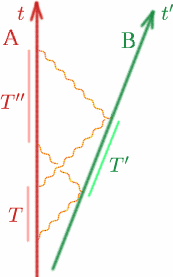
La relazione tra K e la velocità

Sappiamo già che se la velocità relativa di Alf e Ben è zero, allora $K$ = $1$. Qual è il suo valore per le velocità generali? C’è un modo intelligente di risolverlo, che usa l’idea di cui abbiamo appena parlato, più l’idea di simultaneità. Che cosa significa? Lo spiegherò tra un minuto.
Prima di tutto immaginiamo i nostri soliti due osservatori che si allontanano l’uno dall’altro con velocità costante $v$. Supponiamo che quando sono insieme, entrambi impostino i loro orologi su $t = 0$. Al tempo $T$ del suo orologio, Alf emette un segnale radio; Ben lo riflette al tempo $T’$ del suo orologio e Alf lo riceve di nuovo al tempo $T^{primo\primo}$ del suo orologio. Facciamo un disegno come al solito.
?

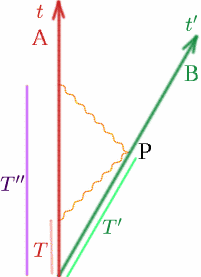
Ora sappiamo che \begin{equazione} {T^{\primo}} = {K T}\quadro (13) \end{equazione} \begin{equazione} {T^{primo}} = {K T^{primo}} = {K^2 T}. \(14) fine della equazione Così Alf pensa che il tempo di percorrenza dell’impulso radio sia \begin{equazione} {T^{prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quadro (15) \end{equazione} e Alf calcola che la distanza, $D$, tra lui e Ben, è la metà della distanza percorsa dal segnale radio, che è metà della velocità per il tempo: \D = 1 {2} c(K^2-1)T}. \(16) fine equazione Ora sappiamo che la distanza tra Alf e Ben cambia costantemente, quindi dobbiamo chiedere quando (cioè in quale momento) questa è la distanza tra Alf e Ben. È qui che abbiamo bisogno dell’idea di simultaneità. La distanza è chiaramente misurata quando Ben si trova nel punto $P$, ma a che tempo corrisponde questo per Alf? Bene, Alf sa che l’impulso radio percorre la stessa distanza all’andata e al ritorno, quindi l’evento $Q$, che Alf giudica essere allo stesso tempo di $P$, sarà a metà strada tra $T$ e $T^{primo\primo}$. (Diciamo che $Q$ è simultaneo a $P$ per Alf – significa semplicemente allo stesso tempo). Quindi il tempo a $Q$ è {T_Q} = {frac {1} {2}(T+T”)} = {frac {1} {2} (K^2+1)T}. \quadrato (17) \fine equazione} Così Alf conclude che Ben ha percorso una distanza $D$ nel tempo $T_Q$, quindi la sua velocità $v$ è data da \begin{equazione} {v} = {\frac {D} {T_Q}} = {frac {frac {1} {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \(18) fine dell’equazione Si ha quindi \begin{equazione} {frac {v} {c}} = {frac {K^2-1} {K^2+1}}. \(19) fine equazione Possiamo ora calcolare $K$ in termini di $ffrac {v} {c}$: \{(K^2+1)\frac {v} {c}} = {K^2-1}, \quadro (20) \fine equazione} \inizio equazione {K^2 \frac{v}{c} + \frac{v}c}} = {K^2-1}, \quadro (21) \fine{equazione} \1+ \frac{v}c} ={K^2(1- \frac{v}c})}, \quadro (22) \end{equazione} Perciò K^2} = {K^2} = {frac {1+ \frac{v}{c} {1- \frac{v}{c}}} e quindi \begin{equazione} {K} = \sqrt{ a sinistra({frac{1+frac{v}{c}}{1- \frac{v}{c}} a destra)}. \quadrato (24) \fine equazione} Prova a calcolare alcuni valori di K:
per esempio $v = c/4$ – che dà $K = \sqrt{5/3} = 1.291$.
Ora prova $v = c/2, 9c/10, 99c/100$.
Ora non importa se Alf è fermo e Ben è in movimento o il contrario – $K$ è ancora lo stesso. Ciò che è diverso è se Alf e Ben si stanno avvicinando l’un l’altro piuttosto che allontanarsi – in quel caso, prendiamo il valore di $v$ per essere negativo, ma possiamo usare la stessa formula.
es. se Alf e Ben si avvicinano l’un l’altro con velocità relativa $c/2$, \begin{equazione} K = \sqrt{{sinistra({frac{1+(-1/2)}{1-(-1/2)}destra)}} = \sqrt{sinistra({frac{1/2}{3/2}}destra)} = \sqrt{1/3}. \(25) fine dell’equazione. Calcoliamo $K$ per alcune velocità tipiche:
1) aerei di linea che si avvicinano l’un l’altro con velocità di $1000km/hr$;
2) galassie nel nostro ammasso che si allontanano con velocità relative di $500km/s$;
3) una macchina che si avvicina a un poliziotto a $100km/hr$;
4) tu che cammini verso un tuo amico a $5km/hr$ Pensi che qualcuno di questi effetti sia osservabile? Il paradosso dei gemelli – finalmente!
Cosa succede? Perché è un paradosso? (Cosa significa la parola paradosso?)
Consideriamo due gemelle identiche, Albertina e Brigitta! Albertina rimane a casa a Londra, mentre Brigitta, quella avventurosa, parte per un viaggio nello spazio. Si allontana dalla Terra per 6 anni, come misurato dal suo orologio, in una nave spaziale molto veloce che viaggia a $v = 4c/5$. Poi ritorna alla stessa velocità per 6 anni. Così Brigitta misura un tempo di 12 anni per il suo viaggio – è 12 anni più vecchia quando torna a casa da Albertina a Londra. Ma quanto è più vecchia Albertina? Vediamo se la tua ipotesi era giusta o forse solo vicina!
Disegniamo un diagramma spazio-temporale: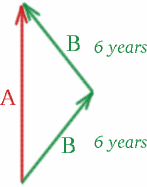
Nel viaggio di andata di Brigitta, i gemelli si allontanano con velocità relativa $v = 4c/5$, per cui \iniziare{equazione} {K^2} = {frac{1+frac{4}{5}}{1-\frac{4}{5}} = {9}, \quadro (26) \fine{equazione} e abbiamo $K=3$. Nel viaggio di ritorno di Brigitta, si avvicinano con la stessa velocità, quindi \inizio equazione} {K^2} = {frac{1-\frac{4}{5}{1+\frac{4}{5}} \quadro (27) \fine equazione} e $K=1/3$. Tutto quello che dobbiamo fare per calcolare il tempo che Albertina misura è mettere un segnale luminoso! Qualche suggerimento su dove?
Supponiamo che Albertina mandi un segnale nel punto $S$, scelto in modo che raggiunga Brigitta a $U$, proprio mentre sta per girare.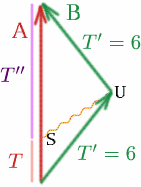
Qual è allora $T$ se $T^{primo}=6$ e $K=3$? Abbiamo \begin{equazione} {T^{primo}} = {K T} \quadro (28) \fine{equazione}
quindi $6=3T$ e $T=2$.
Ora guarda cosa succede nel viaggio di ritorno di Brigitta. Che cos’è $T^{primo\primo\? Abbiamo $T^{prime}=6$, $K=1/3$ e \inizio equazione} {T^{prime}} = {K T^{prime\prime}}, \quadro (29) \fine equazione} quindi $6=T^{prime\prime}/3$ e $T^{prime\prime}=18$. Quindi il tempo totale misurato da Albertina è $T+T^{primo\primo\primo}=20$ anni, quindi lei ha 20 anni in più quando si incontrano, mentre Brigitta ne ha solo 12! Quindi Albertina è invecchiata di 8 anni più di Brigitta!
Allora hai indovinato????
Quello che puoi provare a fare da solo è qualche esperimento con i numeri. Per esempio, puoi immaginare che Brigitta faccia un viaggio di $10+10=20$ anni, e puoi calcolare quanto velocemente deve viaggiare perché Albertina sia invecchiata di un solo anno più di lei (cioè sono passati $21$ anni sull’orologio di Albertina) quando Brigitta ritorna. Forse puoi capire se è possibile che ci sia un viaggio spaziale realistico (cioè realizzabile) in cui i gemelli invecchino in modo diverso di una quantità notevole!
Ora perché tutto questo si chiama paradosso? Ricordate cosa significa paradosso? Abbiamo detto prima che se due persone si muovono a velocità costante (e quindi a velocità costante l’una rispetto all’altra), molto di ciò che accade è lo stesso sia che consideriamo la prima ferma e la seconda in movimento, sia il contrario. Applicando questo ragionamento ad Albertina e Brigitta, perché non possiamo considerare Brigitta nella sua astronave come la persona che sta ferma, e Albertina sulla Terra che si allontana e poi ritorna. Detto così, sembra piuttosto sciocco, ma spero che abbiate capito l’idea. Allora ci aspetteremmo che Brigitta sia più vecchia di Albertina quando finalmente si incontrano. Ma abbiamo già detto che Albertina è più vecchia allora. Come potrebbero essere vere entrambe le affermazioni? Questo è il paradosso!
Vedete cosa c’è di sbagliato?
Il punto è che Brigitta non si muove a velocità costante rispetto ad Albertina per tutto il suo viaggio; ha due lunghi tratti di viaggio in cui lo fa, ma in mezzo c’è un tratto forse breve ma molto importante in cui decelera, si ferma e poi accelera nella direzione opposta. È questo che fa la differenza! L’accelerazione è un fenomeno reale, come probabilmente sapete dalle giostre che vi fanno star male in una fiera! Sapete come si può rilevare con un semplice apparecchio?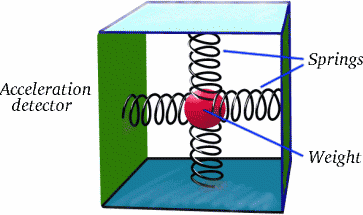
Allora, cosa ne pensa di tutto questo? Sembra un po’ ingiusto che Brigitta viaggi e veda più Universo ma finisca più giovane della sua gemella casalinga – la vita non sembra sempre giusta! Ma dovrebbe incoraggiarti a viaggiare – non necessariamente nello spazio! – e ad essere avventurosi! Riferimento Per ulteriori discussioni sul paradosso dei gemelli e sulle tecniche qui descritte, puoi provare a guardare il libro Flat and Curved Space-Times, di G. F. R. Ellis e me (pubblicato dalla Oxford University Press nel 1988). Potresti anche guardare i libri di Mr. Tompkins che introducono i concetti della relatività speciale in modo divertente e accessibile.

Puoi trovare recensioni dei libri di Mr. Tompkins e ordinarli dal sito della Cambridge University Press, per esempio vedi The New World of Mr Tompkins : George Gamow’s Classic Mr.