Előszó

Ha végigköveted ezt a projektet, elképesztő végkifejletre jutsz! Tegyük fel, hogy egy egypetéjű ikerpár egyik tagja elutazik az űrbe, majd visszatérve összehasonlítja a saját (mondjuk az ő) életkorát a másik ikerpáréval, aki ugyanott maradt a Földön. Kiderül, hogy az utazás után az egyik iker fiatalabb lesz a nővérénél! Bizonyára azt kérdezed, hogyan lehetséges ez, és ennek a projektnek az a célja, hogy megmutassuk, hogyan lehetséges.
Kezdjük egy találgatással – a végén kiderül, hogy igazad volt-e! Tegyük fel, hogy az utazó iker egy 12 éves utazásra indul – 6 év kifelé és 6 év vissza. Nyilvánvalóan 12 évvel lesz idősebb, amikor visszajön. Neked azt kell kitalálnod, hogy a nem utazó ikertestvér mennyivel lesz idősebb….! Meg kell mondanom, hogy a mozgó iker milyen gyorsan utazik – mondjuk a fénysebesség négyötödével -, bár merem állítani, hogy ez nem fog túl sokat segíteni a tippelésben! Hadd javasoljam, hogy tippeljetek egy egész számot 1 és 30 között!
Mielőtt megvizsgálnánk az ikreket, fel kell állítanunk bizonyos eszközöket, amelyekre szükségünk lesz ahhoz, hogy megértsük, mi történik. Sokat fogjuk használni a tér-idő diagramnak nevezett grafikonok egy bizonyos fajtáját. Ne aggódj, ha még soha nem használtál grafikonokat – megpróbáljuk az alapoktól kezdeni.
?

Grafikonok

A legegyszerűbb fajta grafikon csak egy kép arról, ami egy kiválasztott sík felületen történik. Tegyük fel, hogy egy asztalnál vagy íróasztalnál ülsz, és van nálad két vonalzó és egy nagy darab papír. A bal alsó sarokból kiindulva helyezd el az egyik vonalzót az alsó, a másikat a bal oldal mentén felfelé, a papírt pedig helyezd közéjük. Amit kapsz, annak így kell kinéznie:

Azt a pontot, ahol a két vonalzó találkozik (mindkét skálán a nulla), nevezzük origónak, röviden O-nak, a vonalzó pedig a két tengelyt adja . A konvenciót követve az alul elhelyezkedőt nevezzük x-tengelynek, az oldalt felfelé haladót pedig y-tengelynek. A papír bármely pontját megjelölhetjük az $x$ és $y$ értékével, például az origónak $x=0$, $y=0$. Az y-tengelytől 1 cm$-re és az x-tengelytől 2 cm$-re lévő pontnak $x=1$, $y=2$ (ezeket tényleg helyesen írtam!).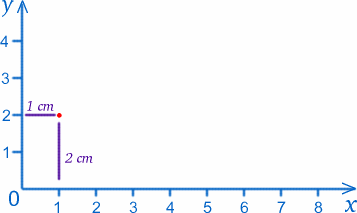

GYakorlat Rajzold meg a saját grafikonodat, és jelöld a következő pontokat:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Milyen alakúak?
Most képzelj el néhány hangyát nagyon piszkos lábakkal. Tegyük fel, hogy az egyik végigsétál a papíron, és mindig $1cm$ távolságban marad az x-tengelytől. Az útja egy egyenes lenne, amelyet az $y=1$ egyenlet ír le (az előző mondatban szavakkal elmondottak szép megfogalmazása). Egy másik mindig $3cm$ távolságra járhat az y-tengelytől; pályájának egyenlete $x=3$ lenne. Egy még eredetibb hangya járhatna úgy, hogy a távolsága mindkét tengelytől mindig azonos legyen; végigmegy $x=1$, $y=1$; $x=2$, $y=2$; stb. és az útját az $x=y$ egyenlet adná meg.

Tér-idő diagramok

Ebben a szakaszban néhány olyan grafikont fogunk rajzolni, amelyek nagyon hasonlítanak az előző szakaszban leírtakra, de a jelentésük meglehetősen eltérő lesz. Továbbra is két tengelyünk van, és az $x$ feliratú továbbra is a távolságot jelöli egy bizonyos irányban. Az eddigi $y$ feliratú tengelyt azonban most $t$-vel jelöljük, ami az időt jelöli, mondjuk másodpercekben mérve.Képzeljünk el például egy labdát, amely az O-tól 3 cm$-re van egy fix ponton; az útja a téridőben az $x=3$ egyenes lesz. Most tegyük fel, hogy a golyó egy egyenes pályán gurul; ekkor a grafikon pontjai a golyó adott időpontokban elfoglalt helyzeteinek felelnek meg, pl. $x=5$, $t=4$ megfelelne annak, hogy a golyó 5cm$-re van az origótól $4$ másodperccel az időmérés kezdete után.
GYakorlat Rajzoljunk pontokat a grafikonra, amelyek a golyó történetének következő eseményeihez tartoznak: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Hogyan értelmeznéd ezt?
Most próbáld meg a $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$ értékeket. Mit veszel észre ezeken a pontokon?
Ha a golyó pályája egyenes vonal a grafikonon, az azt jelenti, hogy a golyó állandó sebességgel (esetleg nulla sebességgel) mozog. Ebben az esetben a sebességet úgy tudjuk kiszámítani, hogy megnézzük, milyen messzire jut a labda egy másodperc alatt – az x-érték változását elosztjuk a t-érték megfelelő változásával. Tehát a második példánkban a labda sebessége $2cm/sec$. Egyetértesz?
GYakorlat Rajzolj egy grafikont, amely egy olyan labda mozgását ábrázolja, amely két pont között állandó sebességgel (de természetesen periodikusan változó irányban) halad előre-hátra.
Most valami meglehetősen furcsa dolgot fogunk csinálni a grafikonunkkal. A speciális relativitáselméletnek nevezett elméletben , ami miatt érdekes az ikrekről és az űrutazásról gondolkodni, gyakran fénysugarakat kell ábrázolnunk a grafikonjainkon. A fénysugarak az üres térben állandó és nagyon nagy (de véges) sebességgel haladnak; a Napról hozzánk érkező fénysugár körülbelül $8$ perccel ezelőtt indult el onnan. (Régebben azt hitték, hogy a fény végtelenül gyorsan terjed, így a csillagokat abban a pillanatban láthatjuk, amikor megfigyeljük őket, de ma már tudjuk, hogy ez tévedés.) Pontosabban, a fény sebessége körülbelül $300000000000000cm/sec$! Ez nagyon furcsa skálákat eredményezhet a tér-idő grafikon tengelyein, ezért a távolságot másképp fogjuk mérni; az x-tengelyen az egységek fénymásodpercek lesznek, azaz a fény által egy másodperc alatt megtett távolság. (Ha az $t$ skála év, a megfelelő x-skála fényév lesz).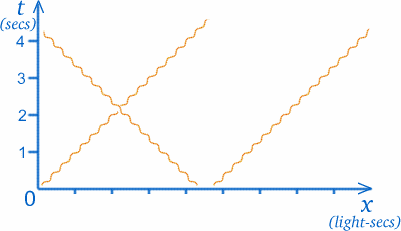
Ennek nagy előnye, hogy egy fénysugár útja mindig $45$ fokban lesz a tengelyekhez képest. Ez azt jelenti, hogy egy O-n áthaladó fénysugár mindkét tengelyhez egyenlő szögben fog állni, ahogy az ábrán látható. (Bár a fény állandó sebességgel halad, így az útja egyenes, mi mégis egy kacskaringós vonallal ábrázoljuk, ahogy az ábrán látható, hogy megkülönböztessük a fénysugarakat más tömegű tárgyak útjától.)
?

Az idő mérése

Hajlamosak vagyunk azt feltételezni, hogy amikor az emberek nem értenek egyet abban, hogy mennyi az idő, akkor valakinek az órája rossz, vagy esetleg az emberek különböző időzónákban vannak! Pedig a dolog ennél sokkal bonyolultabb! A speciális relativitáselmélet szerint két ember lehet ugyanazon a helyen, és korrelálhatnak az óráik, de ha az egyik a másikhoz képest mozog, akkor később nem fognak egyetérteni abban, hogy mennyi az idő. sajnos, ha összeállsz egy barátoddal, és megpróbálod tesztelni ezt az elméletet, csalódni fogsz, de nem azért, mert az elmélet téves, hanem mert azon a sebességen, amit valószínűleg képes leszel futni, még ha szuper atléta is vagy, a hatás túl kicsi lesz ahhoz, hogy megfigyeld. Csak ha a sebességek nagyon nagyok lesznek (a fénysebesség jelentős töredékei), akkor lehet megfigyelni ezt a furcsa jelenséget, és még akkor is csak rendkívül pontos órák használatával.
Hogy lássuk, hogyan működhet ez, nézzünk meg egy “gondolatkísérletet”, hasonlót ahhoz, amit Einstein javasolt. (Ez inkább “gondolatkísérlet”, mint valós kísérlet, mert valójában nem lehet elvégezni, amint azt önök is belátják). Tegyük fel, hogy egy nagyon erős távcsövön keresztül nézzük a Big Ben óráját, miközben távolodunk tőle egy nagyon gyors vonaton, amely pontosan délben halad el az óra mellett (tudom, hogy a vonatok nem mennek el a Big Ben mellett, de tegyünk úgy, mintha!). Ha a vonat fénysebességgel tudna haladni, mit látnátok, mi történne az óra mutatóival? Úgy tűnne, mintha megállnának, és mindkettő a 12$-ra mutatna! Miért? Azért, mert a délben a mutatók által kibocsátott (vagy visszavert) fény pontosan ugyanolyan sebességgel haladna el az órától, mint te a vonaton, és a későbbi időpontokban kibocsátott fény nem tudná utolérni a vonatot! Furcsa!
Megérted, hogy ez miért “gondolatkísérlet” (eltekintve attól a ténytől, hogy a vonatok nem mennek el a Big Ben mellett)? Azért, mert egy vonat valójában nem tudna a fénysebességgel haladni (amit a speciális relativitáselmélet is megmond – bármilyen tárgy, ami bármit is nyom, soha nem tud olyan gyorsan mozogni, mint a fény). De tegyük fel, hogy a vonat a fénysebesség felével halad (ami még mindig nagyon gyors) – látnád, hogy az óra mutatói mozognak, de lassabban, mint az órád mutatói! Az idő mérése attól függ, hogyan mozogsz!
Hogyan lehetséges ez? Hogy ezt megértsük, tekintsünk egy különleges óratípust, a fényórát . Nem valószínű, hogy az ágyad mellett találsz egy ilyet, ami reggel felébreszt. Ez egy fényforrásból áll, amely jeleket bocsát ki, amelyek D távolságot tesznek meg, majd visszaverődnek a fényforráshoz. A jelkibocsátás és a visszaérkezés között eltelt idő határozza meg az óra ketyegését; ezek a ketyegések $2T$ időközönként következnek be, ahol \begin{egyenlet} {T} = {D/c} \end{egyenlet}, ahol $c$ a fénysebességet jelenti. (Ne feledjük, hogy a sebesség = távolság/idő, tehát az idő = távolság/sebesség.)

Tegyük fel, hogy egy mozgó rakétán van egy ilyen óra – a legénység tapasztalata az lesz, hogy a ketyegések $2T$ időközönként következnek be. Most tegyük fel, hogy egy álló rakéta legénysége megfigyeli a mozgó rakéta óráját, és összehasonlítja a sajátjával, amely szintén $2T$ időközönként ketyeg. Mit fognak látni? Az alábbi ábrákból kiderül a válasz. (Sajnálom, hogy a rakétáim inkább halakra hasonlítanak!)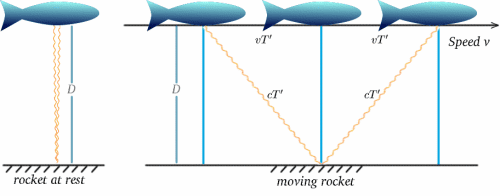
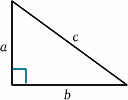
A mozgó rakéta esetében a fény a tükörről a jel elküldése és visszaverődése közötti idő felénél verődik vissza. Az álló rakétáról az utazási idő mondjuk $2T^{ \prime}$-nak tűnik. Ezt egy nagyon fontos tétel (díszes neve annak, amiről a matematikában bebizonyosodott, hogy igaz!) – Pitagorasz tétele – segítségével kiszámíthatjuk.

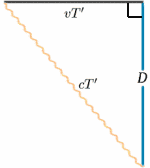\begin{egyenlet} {a^2 + b^2} = {c^2} \quad (1) \end{egyenlet} A rakétadiagramon derékszögű háromszöget kapunk, tehát \begin{egyenlet} D^2 + v^2 T^{‘2} = {c^2 T ^{\prime 2}}\quad (2) \end{egyenlet} Ezt most megoldjuk a $T^{\prime}$-ra: \begin{egyenlet} {T^{\\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{egyenlet} \begin{equation} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{egyenlet} ad \begin{egyenlet} {T^{\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}}\quad (5) \end{egyenlet} és így \begin{egyenlet} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}}, \quad (6) \end{egyenlet} és az órajelek különbözőek lesznek (kivéve persze, ha $v=0$). Valójában $T^{\prime}$ nagyobb, mint $T$, így az álló személyzet számára úgy tűnik, mintha a mozgó óra ketyegései között hosszabbak lennének az intervallumok, tehát lassabban halad.
Mihelyt elfogadjuk, hogy az időnek nincs univerzális, mindenkire érvényes definíciója, el kell gondolkodnunk azon, hogy valójában mit értünk időmérés alatt. Bizonyos értelemben távolságokat mérünk a téridőben megtett utunk mentén (gondoljunk vissza a téridő diagramra). Az ikrek különböző utakat követnek a téridőben, így nem olyan meglepő, hogy különböző mennyiségű időt tapasztaltak.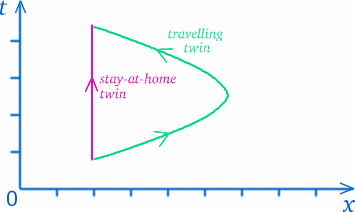
De ne vonjunk le elhamarkodott következtetéseket – a dolgok nem mindig azok, aminek látszanak…! Az utazó iker útja hosszabbnak tűnik, de vajon ez azt jelenti, hogy több időt tapasztalt? Hogy lássuk, mennyire trükkös ez a fajta kérdés, gondoljunk egy olyan helyzetre, amely meglehetősen hasonló lehet. Tegyük fel, hogy Cambridge déli részén, Trumpingtonban laksz, és a városközpont északi szélén lévő Tescóban szeretnél vásárolni (amennyire csak lehet, elkerülve a gyalogos zónákat), a körgyűrűn vagy a kerülőúton – lásd az alábbi ábrát.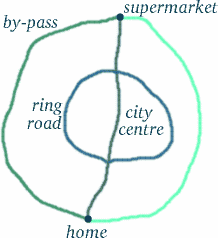
A legtöbb napszakban a leghosszabb útvonal – az elkerülő út – veszi igénybe a legkevesebb időt, ezt követi a körgyűrű. Most már meg van győződve arról, hogy nem mindig a nyilvánvaló válasz a helyes?
Láttuk, hogyan mérik az időt a fényjelzések segítségével. Ha már van egy pontos óránk, akkor a távolságot a távoli objektumról visszavert fény- vagy radarjelek segítségével mérhetjük; a távolság a fény utazási idejének fele lesz, megszorozva a fénysebességgel.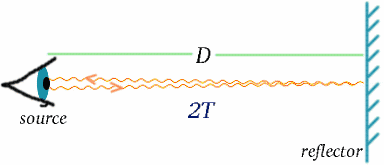

\begin{egyenlet} {D} = {cT}\négyzet (7) \end{egyenlet} Az időhöz hasonlóan a távolság is olyan mennyiség, ahol a mérés eredménye attól függ, hogy a megfigyelő milyen irányban mozog.

K-tényezők

Az alábbiakban egy olyan elképzelést fogok leírni, amelynek segítségével számításokat végezhetünk az általam említett típusú hatásokról.
Tegyük fel, hogy egy űrhajós B (azaz Ben) egy rakétában $c/5$ sebességgel távolodik egy másik űrhajóstól A (azaz Alf) egy űrállomáson. Évente egyszer, március 13-án Alf születésnapi üdvözletet küld Bennek. Tegyük fel, hogy a 2010-es évben ezt az üdvözletet közvetítő rádióüzenet az űrállomás mérése szerint fél fényév távolságot tesz meg, hogy elérje a rakétát, és ehhez fél év kell. A következő üzenetet pontosan egy évvel később küldik el. Amikor ez a rádiójel fél évet utazott addig a helyig, ahol Ben az űrhajós az előző jelet kapta, a rakéta egy fényév ötödével tovább haladt, így ennek a jelnek hosszabb utat kell megtennie, hogy utolérje a rakétát; valójában az Alf által mért idő, amikor a jel eléri a rakétát, háromnegyed évvel a küldés után van – lásd az alábbi ábrát. Szegény Alf arra a következtetésre jut, hogy az évente küldött születésnapi üdvözleteket Alf órája szerint másfél évenként kapja meg Ben.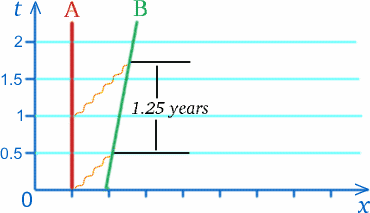
Ez nem árulja el, hogy Ben mit fog mérni ezekben az időközökben, de azt igen, hogy ez nem biztos, hogy egy év lesz! Hasonló hatás fog bekövetkezni a Ben által Alfnak küldött jelek esetében is.
Most nézzük meg az általános esetet, és pontosítjuk ezt. Tekintsünk két megfigyelőt, Alfot és Bent, akik állandó sebességgel távolodnak egymástól.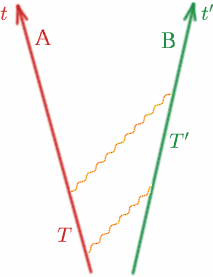
Alf küld egy fényjelet, majd $T$ idővel később egy másikat. Ben az ő órája szerint a két jelet egymástól $T^{\prime}$ távolságra lévő időpontokban fogadja. Ekkor egy $K$ mennyiséget határozunk meg \begin{egyenlet} {K} = {T^{\\prime}/T}. \quad (8) \end{egyenlet} Megjegyezzük, hogy ha Alf és Ben azonos sebességgel (azonos irányban!) mozogna, akkor $K$ egy lenne. Majd meglátjuk, hogy pontosan hogyan függ $K$ Alf és Ben relatív sebességétől. $K$-t néha Doppler-eltolódási tényezőnek is nevezik, és a hatás hasonló a hanghullámokéhoz – bizonyára mindannyian ismeritek a mentő- vagy rendőrautó szirénájának hangjának változását, ahogy közeledik, majd távolodik.
Hogyan tudjuk mérni $K$-t? A legkézenfekvőbb módja az, hogy a megfigyelők feljegyzik a fényjelek küldésének és vételének időpontját, hogy később, amikor találkoznak, kiszámíthassák a $T$ és a $T^{\prime}$, és így a $K$ értékét. Egy másik lehetőség az lenne, ha az egyiknek lenne egy nagyon erős távcsöve, amellyel a másik óráját figyelhetné (ez tényleg a Big Ben mellett elhaladó vonat lenne az egész!).
Meg kell tennünk néhány feltételezést ezzel a $K$ számmal kapcsolatban ahhoz, hogy hasznos legyen számunkra. Először is feltételezzük, hogy amikor Alf és Ben állandó sebességgel mozog, akkor $K$ nem függ attól, hogy mikor mérjük $T$ és $T^{\prime}$, és attól sem, hogy mekkora $T$. Tehát például, ha Alf kétszer annyi időt vár a fényjelek küldése között, a $K$ ugyanannyi lesz. Próbáld meg kitölteni a számokat$T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ ebben az esetben.
?

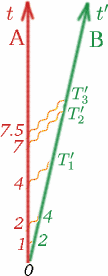
(Vedd észre, hogy az időmérést akkor lehet elkezdeni, amikor a két megfigyelő együtt van, és abban a pillanatban mindketten nullára állíthatják a stopperórájukat). Tehát általánosságban
?

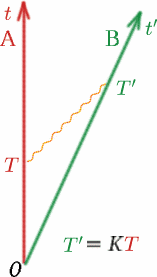
A második dolog, amit feltételezünk, és ami ugyanilyen fontos, hogy a Ben által mért $K$ az Alftól érkező fényjelekre ugyanaz, mint amit Alf a Bentől érkező fényjelekre mért. Miért feltételezzük ezt? Képzeljünk el két egyforma autót egymás mögött egy úton. Az $A$ autó mozdulatlanul áll, a $B$ autó pedig $50km/óra$ sebességgel távolodik az $A$ autótól. Az $A$ hátsó ablakán kinéző utasok azt látják, hogy $B$ a megfelelő sebességgel eltűnik. A $B$ utasai nagyon hasonló képet látnak, ha a hátsó ablakon keresztül néznek be – az $A$ autó ugyanolyan sebességgel távolodik! Volt már olyan hátborzongató élménye, amikor egy vonaton ülve azt hitte, hogy a vonat éppen elindult, amikor kiderült, hogy a szomszédos vonat indult el az ellenkező irányba, és az ön vonata még mindig álló helyzetben van?
Ez a feltételezés lehetővé teszi, hogy az egyik megfigyelő radarral mérje a $K$-t anélkül, hogy a másik együttműködne vele. Ki tudja valaki kitalálni, hogyan? Hadd adjak egy tippet.
Tegyük fel a szokásos módon, hogy Alf és Ben állandó sebességgel távolodnak egymástól. Alf két jelet küld ki $T$ időközönként, Ben ezeket $T^{\prime}$ időközönként visszaveri, Alf pedig $T^{\prime\prime}$ időközönként fogadja vissza. Hogyan tudja Alf kiszámítani $K$-t?
?

Válasz

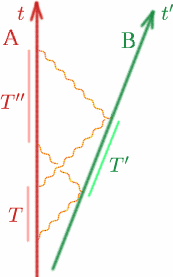
\begin{egyenlet} {T^{\\prime}} = {K T} \quad (9), \end{egyenlet} \begin{egyenlet} {T^{\prime\prime}} = {K T^{\prime}}\négyzet (10) \end{egyenlet} Tehát \begin{egyenlet} {T^{\prime\prime}} = {K(K T)} = {K^2 T}\négyzet (11) \end{egyenlet} tehát \begin{egyenlet} {K} = {\sqrt{T^{\prime\prime}/T}}}. \négyzet (12) \end{egyenlet} Probléma A bonyolult dokkolási manőver végrehajtásához elengedhetetlen, hogy a két űrhajót egymáshoz képest nyugalomban tartsuk. Tervezzünk egy egyszerű kísérletet annak ellenőrzésére, hogy ez így van-e.

A K és a sebesség kapcsolata

Már tudjuk, hogy ha Alf és Ben relatív sebessége nulla, akkor $K$ = $1$. Mi az értéke általános sebességek esetén? Van egy okos módja ennek a kiszámításának, amely az imént tárgyalt gondolatot, valamint az egyidejűség gondolatát használja. Ez mit jelent? Egy perc múlva elmagyarázom.
Először is képzeljük el a szokásos két megfigyelőnket, akik állandó $v$ sebességgel távolodnak egymástól. Tegyük fel, hogy amikor együtt vannak, mindketten $t = 0$-ra állítják az órájukat. Alf az ő órája szerint $T$ időpontban Alf rádiójelet bocsát ki; Ben az ő órája szerint $T’$ időpontban visszaveri azt, Alf pedig az ő órája szerint $T^{\\prime\prime}$ időpontban kapja vissza. Rajzoljunk egy képet a szokásos módon.
?

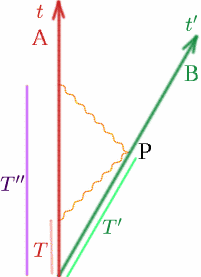
Most már tudjuk, hogy \begin{egyenlet} {T^{\prime}} = {K T}\quad (13) \end{egyenlet} \begin{equation} {T^{\prime\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{egyenlet} Alf tehát úgy gondolja, hogy a rádióimpulzus utazási ideje \begin{egyenlet} {T^{\\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{egyenlet} és Alf kiszámítja, hogy a távolság, $D$, közte és Ben között a rádiójel által megtett távolság fele, ami a sebesség fele szorozva az idővel: \begin{egyenlet} {D} = {\frac {1} {2} c(K^2-1)T}. \quad (16) \end{egyenlet} Most már tudjuk, hogy az Alf és Ben közötti távolság folyamatosan változik, ezért meg kell kérdeznünk, hogy mikor (azaz milyen időpontban) ez a távolság Alf és Ben között. Itt van szükségünk a szimultaneitás gondolatára. A távolságot egyértelműen akkor mérjük, amikor Ben a $P$ pontban van, de ez Alf számára milyen időpontnak felel meg? Nos, Alf tudja, hogy a rádióimpulzus ugyanolyan távolságot tesz meg kifelé és vissza, így a $Q$ esemény, amelyről Alf úgy ítéli meg, hogy ugyanabban az időben van, mint $P$, félúton lesz $T$ és $T^{\\prime\prime}$ között. (Azt mondjuk, hogy Alf számára $Q$ egyidejűleg történik $P$-vel – ez csak azt jelenti, hogy egy időben). Tehát az idő $Q$-nál \begin{egyenlet} {T_Q} = {\frac {1} {2}(T+T”’)} = {\frac {1} {2} (K^2+1)T}. \quad (17) \end{egyenlet} Alf tehát arra a következtetésre jut, hogy Ben $D$ távolságot tett meg $T_Q$ idő alatt, így a sebességét $v$ a \begin{egyenlet} {v} = {\frac {D} {T_Q}} = {\frac {\frac {\frac {1}} {\frac {1}{2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \quad (18) \end{egyenlet} Ezért \begin{equation} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \quad (19) \end{egyenlet} Most már ki tudjuk számítani $K$-t a $\frac {v} {c}$ függvényében: \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{egyenlet} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Tehát \begin{egyenlet} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}}\négyzet (23) \end{egyenlet} és így \begin{egyenlet} {K} = \sqrt{{{\left({\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}\right)}}. \quad (24) \end{egyenlet} Próbáljuk ki K néhány értékét:
pl. $v = c/4$ – ez $K = \sqrt{5/3} = 1.291$.
Most próbáljuk ki $v = c/2, 9c/10, 99c/100$.
Most már mindegy, hogy Alf mozdulatlanul áll, Ben pedig mozog, vagy fordítva – $K$ akkor is ugyanaz. Más a helyzet, ha Alf és Ben inkább közelednek egymáshoz, mint távolodnak egymástól – ebben az esetben a $v$ értékét negatívnak vesszük, de ugyanezt a képletet használhatjuk.
pl. ha Alf és Ben relatív sebességgel $c/2$ közeledik egymáshoz, \begin{equation} K = \sqrt{\left({\frac{1+(-1/2)}{1-(-1/2)}}}\right)}} = \sqrt{{\left({\frac{1/2}{3/2}}}\right)}} = \sqrt{1/3}. \quad (25) \end{egyenlet}. Számoljuk ki $K$-t néhány tipikus sebességre:
1) 1000km/óra sebességgel közeledő utasszállító repülőgépek$;
2) a halmazunkban lévő galaxisok $500km/s$ relatív sebességgel távolodnak egymástól;
3) egy rendőrhöz $100km/óra sebességgel közeledő autó$;
4) Ön 5km/óra sebességgel sétál a barátja felé$ Ön szerint ezek közül bármelyik hatás megfigyelhető lenne? Az ikerparadoxon – végre!
Mi történik? Miért paradoxon ez? (Mit jelent egyáltalán a paradoxon szó?)
Lássuk az egypetéjű ikreket, Albertinát és Brigittát! Albertina otthon marad Londonban, míg Brigitta, a kalandvágyó, űrutazásra indul. Az órája által mért 6 évig utazik távol a Földtől egy nagyon gyors űrhajóval, amely $v = 4c/5$ sebességgel halad. Ezután ugyanezzel a sebességgel tér vissza 6 évre. Brigitta tehát 12 évet mér az utazása alatt – 12 évvel idősebb, mire hazaér Albertinához Londonba. De mennyivel idősebb Albertina? Lássuk, hogy a tipped helyes volt-e, vagy talán csak közel volt hozzá!
Rajzoljunk egy tér-idő diagramot: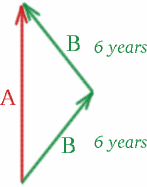
Brigitta kifelé tartó útján az ikrek $v = 4c/5$ relatív sebességgel távolodnak egymástól, így \begin{egyenlet} {K^2} = {\frac{1+\frac{4}{5}}}{1-\frac{4}{5}}}} = {9}, \quad (26) \end{egyenlet} és $K=3$. Brigitta visszaúton ugyanolyan sebességgel közelítik meg egymást, így \begin{egyenlet} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}}\quad (27) \end{egyenlet} és $K=1/3$. Mindössze annyit kell tennünk, hogy kiszámoljuk az Albertina által mért időt, hogy egy fényjelet teszünk be! Valami javaslat, hogy hova?
Tegyük fel, hogy Albertina egy jelet küld a $S$ ponton, amelyet úgy választunk ki, hogy az éppen akkor érje el Brigittát az $U$ ponton, amikor az éppen megfordulni készül.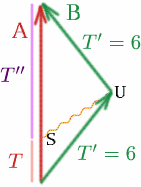
Ezután mennyi a $T$, ha $T^{\prime}=6$ és $K=3$? Van \begin{egyenlet} {T^{\\prime}} = {K T} \quad (28) \end{egyenlet}
szóval $6=3T$ és $T=2$.
Most nézzük meg, mi történik Brigitta visszaútján. Mennyi a $T^{\\prime\prime}$? Van $T^{\prime}=6$, $K=1/3$ és \begin{egyenlet} {T^{\prime}} = {K T^{\prime\prime}}, \quad (29) \end{egyenlet} tehát $6=T^{\prime\prime}/3$ és $T^{\prime\prime}=18$. Ezért az Albertina által mért teljes idő $T+T^{\prime\prime}=20$ év, tehát ő 20 évvel idősebb, amikor találkoznak, míg Brigitta csak12 évvel! Tehát Albertina 8 évvel többet öregedett, mint Brigitta!
Szóval jól tippeltél????
Mit egyedül is megpróbálhatsz, az néhány kísérlet a számokkal. Például elképzelheted, hogy Brigitta mondjuk 10+10=20$ évet utazik, és kiszámolhatod, hogy milyen gyorsan kell utaznia ahhoz, hogy Albertina csak egy évvel öregedett többet, mint ő (azaz Albertina óráján 21$ év telt el), mire Brigitta visszatér. Talán ki tudod számolni, hogy lehetséges lenne-e olyan reális (azaz megvalósítható) űrutazás, amely során az ikrek észrevehetően eltérő mértékben öregednének!
Most miért nevezik mindezt paradoxonnak ? Emlékszel mit jelent a paradoxon ? Korábban azt mondtuk, hogy ha két ember állandó sebességgel (és így egymáshoz képest állandó sebességgel) mozog, akkor sok minden ugyanúgy történik, akár az elsőt tekintjük állónak, a másodikat mozgónak, akár fordítva. Ezt az érvet Albertinára és Brigittára alkalmazva,miért nem tekinthetjük Brigittát az űrhajójában álló személynek, Albertinát pedig a Földön elhajózó, majd visszatérő személynek. Így megfogalmazva elég bután hangzik, de remélem, érted a lényeget. Akkor azt várnánk, hogy Brigitta idősebb legyen Albertinánál, amikor végre találkoznak. De már mondtuk, hogy Albertina akkor már idősebb. Hogyan lehetne mindkét állítás igaz? Ez aparadoxon!
Azt látod, hogy mi a baj?
A lényeg az, hogy Brigitta nem halad állandó sebességgel Albertinához képest az egész útja során; van két hosszú útszakasza, ahol ezt teszi, de a kettő között van egy esetleg rövid, de nagyon fontos szakasz, ahol lelassul, megáll, majd az ellenkező irányba gyorsul. Ez az, ami mindent megváltoztat!!! A gyorsulás egy valódi jelenség, ahogyan azt valószínűleg tudjátok a vásárokon a rosszullétet okozó hullámvasutakról! Tudod, hogyan lehet ezt egy egyszerű eszközzel kimutatni?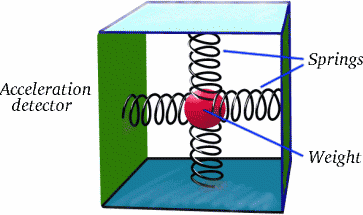
Mit gondolsz minderről? Kicsit igazságtalannak tűnik, hogy Brigitta utazhat és többet láthat az Univerzumból, de végül fiatalabb lesz, mint az otthon maradó ikertestvére – az élet nem mindig tűnik igazságosnak! De ez arra kellene, hogy ösztönözzön, hogy utazzon – nem feltétlenül az űrben! – és legyetek kalandvágyóak! Hivatkozás Az ikerparadoxonról és az itt leírt technikákról bővebben G. F. R. Ellis és jómagam Flat and Curved Space-Times című könyvében olvashatsz (1988-ban jelent meg az Oxford University Press kiadónál). Megnézheted a Tompkins úr könyveit is, amelyek szórakoztató és közérthető módon mutatják be a speciális relativitáselmélet fogalmait.

A Tompkins úr könyveiről kritikákat találsz, és megrendelheted őket a Cambridge University Press honlapján, például lásd: The New World of Mr Tompkins : George Gamow’s Classic Mr. Tompkinsin Paperback

.