Einleitung

Wenn Sie dieses Projekt weiterverfolgen, werden Sie zu einer erstaunlichen Schlussfolgerung geführt! Nehmen wir an, einer der beiden eineiigen Zwillinge begibt sich auf eine Reise in den Weltraum und kehrt dann zurück, um sein (sagen wir ihr) Alter mit dem des anderen Zwillings zu vergleichen, der am selben Ort auf der Erde geblieben ist. Es stellt sich heraus, dass der eine Zwilling nach der Reise jünger ist als seine Schwester! Du fragst dich sicher, wie das möglich ist, und das Ziel dieses Projekts ist es, dir zu zeigen, wie das geht.
Beginnen wir mit einem Ratespiel – wir werden am Ende herausfinden, ob du richtig liegst! Angenommen, der reisende Zwilling geht auf eine 12-jährige Reise – 6 Jahre hin und 6 Jahre zurück. Natürlich wird sie 12 Jahre älter sein, wenn sie zurückkommt. Sie müssen nun erraten, wie viel älter der nicht reisende Zwilling sein wird….! Ich muss dir sagen, wie schnell der sich bewegende Zwilling reist – sagen wir vier Fünftel der Lichtgeschwindigkeit – obwohl ich wage zu behaupten, dass dir das bei deiner Schätzung nicht allzu sehr helfen wird! Ich schlage vor, dass du eine ganze Zahl zwischen 1 und 30 errätst!
Bevor wir uns mit den Zwillingen beschäftigen, müssen wir uns einige Hilfsmittel zulegen, die wir brauchen, um zu verstehen, was vor sich geht. Wir werden viel Gebrauch von einer bestimmten Art von Diagramm machen, dem sogenannten Raum-Zeit-Diagramm. Machen Sie sich keine Sorgen, wenn Sie noch nie mit Graphen gearbeitet haben – wir werden versuchen, mit den Grundlagen zu beginnen.
…

Graphen

Die einfachste Art von Graphen ist nur ein Bild dessen, was auf einer ausgewählten flachen Oberfläche geschieht. Nehmen wir an, du sitzt an einem Tisch oder einem Schreibtisch und hast zwei Lineale und ein großes Blatt Papier. Beginnen Sie in der linken unteren Ecke und legen Sie ein Lineal an der Unterseite und eines an der linken Seite entlang, wobei das Papier dazwischen liegt. Das Ergebnis sollte folgendermaßen aussehen:

Den Punkt, an dem sich die beiden Lineale treffen (der Nullpunkt auf beiden Skalen), nennen wir den Ursprung, kurz O, und die Lineale bilden die beiden Achsen. Der Konvention folgend bezeichnen wir die Achse entlang der Unterseite als x-Achse und die Achse entlang der Seite als y-Achse. Wir können jeden Punkt auf dem Papier mit den Werten $x$ und $y$ bezeichnen, z.B. hat der Ursprung $x=0$, $y=0$. Der Punkt $1cm$ von der y-Achse und $2cm$ von der x-Achse hat $x=1$, $y=2$ (ich habe das wirklich richtig herum!).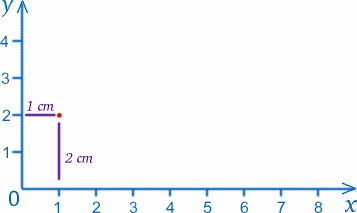

Übung Zeichne deinen eigenen Graphen und markiere die folgenden Punkte:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Welche Form bilden sie?
Nun stelle dir einige Ameisen mit sehr schmutzigen Füßen vor. Nehmen wir an, eine läuft über das Papier und bleibt dabei immer $1cm$ von der x-Achse entfernt. Ihr Weg wäre eine Linie, die durch die Gleichung $y=1$ beschrieben wird (eine schöne Umschreibung für das, was im vorigen Satz in Worten gesagt wurde). Eine andere könnte immer $3cm$ von der y-Achse entfernt laufen; die Gleichung ihrer Bahn wäre $x=3$. Eine etwas originellere Ameise könnte so laufen, dass ihr Abstand von beiden Achsen immer gleich ist; sie würde durch $x=1$, $y=1$; $x=2$, $y=2$; usw. gehen und ihr Weg wäre durch die Gleichung $x=y$ gegeben.

Raum-Zeit-Diagramme

In diesem Abschnitt werden wir einige Diagramme zeichnen, die denjenigen im vorherigen Abschnitt sehr ähnlich sehen, aber ihre Bedeutung wird etwas anders sein. Wir haben immer noch zwei Achsen, und die mit $x$ beschriftete steht immer noch für die Entfernung in einer bestimmten Richtung. Die mit $y$ beschriftete Achse ist nun jedoch mit $t$ beschriftet und steht für die Zeit, z.B. gemessen in Sekunden. Stellen Sie sich z.B. einen Ball vor, der sich an einem festen Punkt $3cm$ von O entfernt befindet; seine Bahn in der Raumzeit ist die Gerade $x=3$. Nehmen wir nun an, der Ball rollt auf einer geraden Bahn; dann würden Punkte auf dem Graphen Positionen des Balls zu bestimmten Zeitpunkten entsprechen, z.B. $x=5$, $t=4$ würde bedeuten, dass der Ball $5cm$ vom Ursprung $4$ Sekunden nach Beginn der Zeitmessung entfernt ist.
Übung Zeichnen Sie Punkte auf den Graphen, die den folgenden Ereignissen in der Geschichte des Balls entsprechen: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Wie würden Sie das interpretieren?
Nun versuchen Sie $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Was fällt Ihnen an diesen Punkten auf?
Wenn der Weg des Balls eine gerade Linie auf dem Graphen ist, bedeutet das, dass sich der Ball mit konstanter Geschwindigkeit (vielleicht Geschwindigkeit Null) bewegt. In diesem Fall können wir die Geschwindigkeit berechnen, indem wir sehen, wie weit der Ball in einer Sekunde kommt – wir dividieren die Änderung des x-Wertes durch die entsprechende Änderung des t-Wertes. In unserem zweiten Beispiel beträgt die Geschwindigkeit des Balles also $2cm/sec$. Sind Sie einverstanden?
Übung Zeichnen Sie einen Graphen, der die Bewegung einer Kugel darstellt, die sich zwischen zwei Punkten mit konstanter Geschwindigkeit hin- und herbewegt (aber natürlich periodisch die Richtung ändert).
Wir werden nun etwas ziemlich Seltsames mit unserem Graphen machen. In der speziellen Relativitätstheorie, die es interessant macht, über Zwillinge und Raumfahrt nachzudenken, müssen wir oft Lichtstrahlen in unsere Diagramme einzeichnen. Nun bewegen sich Lichtstrahlen im leeren Raum mit einer konstanten und sehr großen (aber endlichen) Geschwindigkeit; ein Lichtstrahl, der Sie von der Sonne erreicht, hat diese vor etwa $8$ Minuten verlassen. (Früher glaubte man, dass sich Licht unendlich schnell bewegt, so dass man die Sterne in dem Moment sehen konnte, in dem man sie beobachtete, aber das ist heute bekanntlich falsch.) Um genauer zu sein, beträgt die Lichtgeschwindigkeit etwa $30000000000cm/sec$! Das könnte zu sehr merkwürdigen Skalen auf den Achsen eines Raum-Zeit-Diagramms führen, also werden wir die Entfernung auf eine andere Art und Weise messen; die Einheiten auf der x-Achse werden Lichtsekunden sein, d.h. die Entfernung, die das Licht in einer Sekunde zurücklegt. (Wenn die Skala für $t$ Jahre ist, ist die entsprechende x-Skala Lichtjahre.)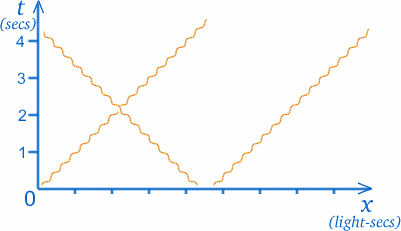
Der große Vorteil dabei ist, dass der Weg eines Lichtstrahls immer in einem Winkel von $45$ zu den Achsen steht. Das bedeutet, dass ein Lichtstrahl durch O in gleichen Winkeln zu beiden Achsen verläuft, wie man im Diagramm sehen kann. (Obwohl sich das Licht mit konstanter Geschwindigkeit fortbewegt und sein Weg eine gerade Linie ist, stellen wir ihn, wie gezeigt, durch eine gewundene Linie dar, um Lichtstrahlen von den Wegen anderer Objekte mit Masse zu unterscheiden.)
?

Zeitmessung

Wir neigen zu der Annahme, dass, wenn die Leute sich nicht einig sind, wie spät es ist, die Uhr von jemandem falsch geht, oder vielleicht befinden sich die Leute in verschiedenen Zeitzonen! Aber es ist noch komplizierter als das! Wenn Sie sich mit einem Freund zusammentun und versuchen, diese Theorie zu testen, werden Sie leider enttäuscht sein, nicht weil die Theorie falsch ist, sondern weil bei der Geschwindigkeit, mit der Sie wahrscheinlich laufen können, selbst wenn Sie ein Supersportler sind, der Effekt zu gering ist, um ihn zu beobachten. Erst wenn die Geschwindigkeiten sehr groß werden (beträchtliche Bruchteile der Lichtgeschwindigkeit), kann dieses seltsame Phänomen beobachtet werden, und selbst dann nur unter Verwendung extrem genauer Uhren.
Um zu sehen, wie dies funktionieren könnte, betrachten wir ein „Gedankenexperiment“, das dem von Einstein vorgeschlagenen ähnelt. (Es handelt sich um ein „Gedankenexperiment“ und nicht um ein reales Experiment, weil es, wie Sie feststellen werden, nicht wirklich durchgeführt werden kann.) Nehmen wir an, Sie beobachten die Uhr am Big Ben durch ein sehr leistungsfähiges Teleskop, während Sie sich in einem sehr schnellen Zug von ihr entfernen, der genau zur Mittagszeit an der Uhr vorbeifährt (ich weiß, dass Züge nicht direkt am Big Ben vorbeifahren, aber tun wir einfach so!) Wenn der Zug nun mit Lichtgeschwindigkeit fahren könnte, was würde dann mit den Zeigern der Uhr passieren? Sie würden scheinbar stillstehen, beide zeigen auf $12$! Und warum? Weil das Licht, das von den Zeigern zur Mittagszeit ausgestrahlt (oder reflektiert) wird, sich mit genau der gleichen Geschwindigkeit von der Uhr wegbewegen würde wie du im Zug, und das Licht, das zu einem späteren Zeitpunkt ausgestrahlt wird, könnte den Zug nicht mehr einholen! Seltsam!
Verstehen Sie, warum das ein „Gedankenexperiment“ ist (ganz abgesehen davon, dass Züge nicht am Big Ben vorbeifahren)? Der Grund ist, dass sich ein Zug nicht mit Lichtgeschwindigkeit fortbewegen kann (was uns die spezielle Relativitätstheorie ebenfalls sagt – ein Objekt, das etwas wiegt, kann sich niemals so schnell wie das Licht bewegen). Aber nehmen wir an, der Zug würde sich mit halber Lichtgeschwindigkeit bewegen (immer noch sehr schnell) – Sie würden sehen, wie sich die Zeiger der Uhr bewegen, aber langsamer als die Ihrer Uhr! Die Messung der Zeit hängt davon ab, wie man sich bewegt!
Wie kann das sein? Um dies zu verstehen, betrachten wir eine besondere Art von Uhr, eine Lichtuhr. Es ist unwahrscheinlich, dass Sie eine solche Uhr neben Ihrem Bett finden, wenn Sie morgens geweckt werden. Sie besteht aus einer Lichtquelle, die Signale aussendet, die eine Strecke D zurücklegen und dann zur Quelle reflektiert werden. Die Zeitlücke oder das Intervall zwischen dem Aussenden eines Signals und dem Rückempfang definiert die Ticks der Uhr; sie treten im Abstand von $2T$ auf, wobei \begin{equation} {T} = {D/c} \end{equation}, wobei $c$ die Lichtgeschwindigkeit darstellt. (Zur Erinnerung: Geschwindigkeit = Entfernung/Zeit, also Zeit = Entfernung/Geschwindigkeit.)

Nehmen wir nun an, dass eine sich bewegende Rakete eine solche Uhr trägt – die Erfahrung der Besatzung wird sein, dass die Ticks in Abständen von $2T$ auftreten. Nehmen wir nun an, die Besatzung einer stationären Rakete beobachtet die Uhr der sich bewegenden Rakete und vergleicht sie mit ihrer eigenen, die ebenfalls in Intervallen von $2T$ tickt. Was werden sie sehen? Die folgenden Diagramme sollten die Antwort nahelegen. (Es tut mir leid, dass meine Raketen eher wie Fische aussehen!)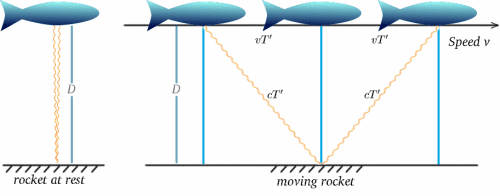
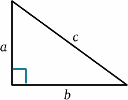
Für die sich bewegende Rakete wird das Licht vom Spiegel in der Hälfte der Zeit zwischen dem Senden des Signals und dem Zurückwerfen reflektiert. Bei der stationären Rakete scheint die Reisezeit etwa $2T^{ \prime}$ zu betragen. Wir können dies mit Hilfe eines sehr wichtigen Satzes (ein schicker Name für etwas, das in der Mathematik als wahr erwiesen wurde!) berechnen – dem Satz des Pythagoras.

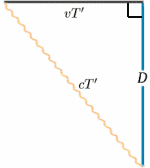\begin{equation} {a^2 + b^2} = {c^2} \quad (1) \end{equation} Im Raketendiagramm haben wir ein rechtwinkliges Dreieck, also \begin{equation} D^2 + v^2 T^{‚2} = {c^2 T ^{\{prime 2}}\quad (2) \end{equation} Wir lösen dies nun für $T^{\{prime}$: \begin{equation} {T^{\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \begin{equation} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{equation} ergibt \begin{equation} {T^{\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}\quad (5) \end{equation} und somit \begin{equation} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}, \quad (6) \end{equation} und die Taktraten werden unterschiedlich sein (es sei denn natürlich $v=0$). Tatsächlich ist $T^{\prime}$ größer als $T$, so dass es für die stationäre Besatzung so aussieht, als ob die bewegte Uhr längere Intervalle zwischen den Ticks hat und daher langsamer geht.
Wenn wir akzeptieren, dass es keine universelle Definition der Zeit gibt, die für alle gilt, müssen wir darüber nachdenken, was wir wirklich mit Zeitmessung meinen. In gewissem Sinne messen wir Entfernungen entlang unserer Wege in der Raumzeit (denken Sie an das Raum-Zeit-Diagramm). Die Zwillinge gehen unterschiedliche Wege in der Raumzeit, also ist es nicht so überraschend, dass sie unterschiedliche Zeitspannen erlebt haben.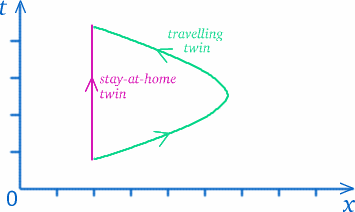
Aber ziehen Sie keine voreiligen Schlüsse – die Dinge sind nicht immer so, wie sie scheinen…! Der Weg des reisenden Zwillings sieht länger aus, aber bedeutet das, dass er mehr Zeit erlebt hat? Um zu sehen, wie knifflig diese Art von Frage ist, denke an eine Situation, die ziemlich ähnlich sein könnte. Nehmen wir an, Sie wohnen in Trumpington, im Süden von Cambridge, und wollen im Tesco’s am nördlichen Rand des Stadtzentrums einkaufen (so weit wie möglich, unter Vermeidung von Fußgängerzonen), auf der Ringstraße oder auf der Umgehungsstraße – siehe das Diagramm unten.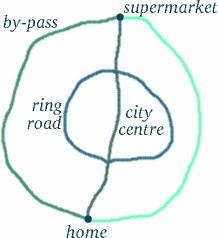
Zu den meisten Tageszeiten würden Sie feststellen, dass die längste Strecke – die Umgehungsstraße – die wenigste Zeit in Anspruch nimmt, gefolgt von der Ringstraße. Bist du nun überzeugt, dass die offensichtliche Antwort nicht immer die richtige ist?
Wir haben gesehen, wie die Zeit mit Hilfe von Lichtsignalen gemessen wird. Wenn wir eine genaue Uhr haben, können wir die Entfernung mit Hilfe von Licht- oder Radarsignalen messen, die von einem entfernten Objekt reflektiert werden; die Entfernung ist die Hälfte der Lichtlaufzeit, multipliziert mit der Lichtgeschwindigkeit.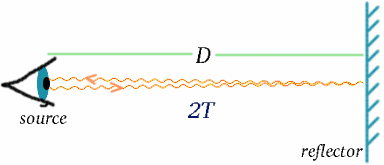

\begin{equation} {D} = {cT}\quad (7) \end{equation} Wie die Zeit ist auch die Entfernung eine Größe, bei der das Ergebnis der Messung davon abhängt, wie sich der Beobachter bewegt.

K-Faktoren

Ich werde jetzt eine Idee beschreiben, die uns helfen soll, Berechnungen der Art von Effekten durchzuführen, von denen ich erzählt habe.
Angenommen, ein Astronaut B (für Ben) befindet sich in einer Rakete, die sich mit der Geschwindigkeit $c/5$ von einem anderen Astronauten A (für Alf) auf einer Raumstation entfernt. Einmal im Jahr, am 13. März, sendet Alf Geburtstagsgrüße an Ben. Nehmen wir an, dass der Funkspruch, der diesen Gruß im Jahr 2010 übermittelt, von der Raumstation über eine Entfernung von einem halben Lichtjahr gemessen wird und ein halbes Jahr braucht, um die Rakete zu erreichen. Die nächste Nachricht wird genau ein Jahr später gesendet. Wenn dieses Funksignal ein halbes Jahr lang bis zu der Stelle gereist ist, an der Ben, der Astronaut, das vorherige Signal empfangen hat, hat sich die Rakete um ein Fünftel eines Lichtjahres weiterbewegt, so dass dieses Signal länger unterwegs sein muss, um die Rakete einzuholen; tatsächlich ist der von Alf gemessene Zeitpunkt, an dem das Signal die Rakete erreicht, ein dreiviertel Jahr nach dem Senden – siehe das Diagramm unten. Der arme Alf folgert daraus, dass die jährlich gesendeten Geburtstagsgrüße nach Alfs Uhr im Abstand von eineinviertel Jahren bei Ben ankommen werden.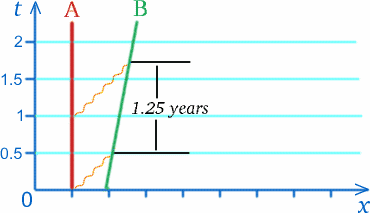
Das sagt uns zwar nicht, was Ben in diesen Intervallen messen wird, aber es deutet darauf hin, dass es nicht unbedingt ein Jahr sein muss! Ein ähnlicher Effekt tritt bei Signalen auf, die von Ben an Alf gesendet werden.
Betrachten wir nun den allgemeinen Fall und präzisieren wir ihn. Betrachten wir zwei Beobachter Alf und Ben, die sich mit konstanter Geschwindigkeit voneinander entfernen.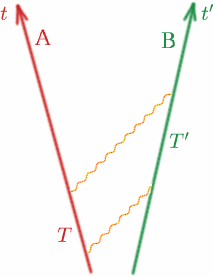
Alf sendet ein Lichtsignal und dann ein weiteres zum Zeitpunkt $T$ später. Ben empfängt die beiden Signale zu Zeiten $T^{\prime}$, die nach seiner Uhr auseinander liegen. Dann definieren wir eine Größe $K$ durch \begin{equation} {K} = {T^{\prime}/T}. \quad (8) \end{equation} Man beachte, dass, wenn Alf und Ben sich mit derselben Geschwindigkeit (in dieselbe Richtung!) bewegen würden, $K$ eins wäre. Wir werden später genau sehen, wie $K$ von der relativen Geschwindigkeit von Alf und Ben abhängt. $K$ wird manchmal als Doppler-Verschiebungsfaktor bezeichnet, und der Effekt ist ähnlich wie bei Schallwellen – Sie kennen sicher alle die Veränderung des Klangs der Sirene eines Krankenwagens oder eines Polizeiautos, wenn es sich nähert und dann wieder entfernt.
Wie können wir $K$ messen? Die naheliegendste Möglichkeit ist, dass die Beobachter Aufzeichnungen darüber führen, wann die Lichtsignale gesendet und empfangen werden, so dass sie $T$ und $T^{\{prime}$ und damit $K$ berechnen können, wenn sie sich später treffen. Eine andere Möglichkeit wäre, dass der eine ein sehr leistungsfähiges Teleskop hat, mit dem er die Uhr des anderen beobachten kann (das ist wirklich wie der Zug, der am Big Ben vorbeifährt!).
Wir müssen einige Annahmen über diese Zahl $K$ machen, damit sie für uns nützlich ist. Wir nehmen zunächst an, dass, wenn Alf und Ben sich mit konstanter Geschwindigkeit bewegen, $K$ weder davon abhängt, wann $T$ und $T^{\prime}$ gemessen werden, noch davon, wie groß $T$ ist. Wenn Alf also zum Beispiel doppelt so lange zwischen dem Senden von Lichtsignalen wartet, wird $K$ gleich sein. Versuchen Sie, die Zahlen $T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ in diesem Fall einzutragen.
?

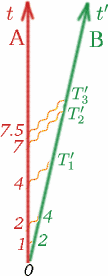
(Beachten Sie, dass es in Ordnung ist, mit der Zeitmessung zu beginnen, wenn die beiden Beobachter zusammen sind, und sie können beide ihre Stoppuhren in diesem Moment auf Null stellen.) Im Allgemeinen haben wir also
?

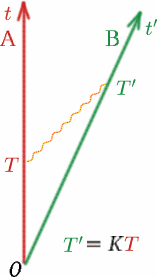
Die zweite Annahme, die ebenso wichtig ist, ist, dass der von Ben gemessene $K$ für Lichtsignale von Alf derselbe ist wie der von Alf gemessene für Lichtsignale von Ben. Warum nehmen wir das an? Stellen Sie sich zwei identische Autos vor, die Rücken an Rücken auf einer Straße fahren. Auto $A$ bleibt stehen und Auto $B$ fährt mit $50km/Std$ von $A$ weg. Die Passagiere, die durch die Heckscheibe von $A$ schauen, werden $B$ mit der entsprechenden Geschwindigkeit verschwinden sehen. Die Passagiere in $B$ werden ein sehr ähnliches Bild sehen, wenn sie durch ihr Heckfenster schauen – Auto $A$ scheint sich mit der gleichen Geschwindigkeit zu entfernen! Haben Sie schon einmal die unheimliche Erfahrung gemacht, in einem Zug zu sitzen und zu denken, er sei gerade losgefahren, wenn sich herausstellt, dass es der Nachbarzug war, der sich in die entgegengesetzte Richtung bewegte, während Ihr Zug immer noch stillsteht?
Diese Annahme macht es möglich, dass ein Beobachter $K$ per Radar messen kann, ohne dass der andere mitarbeitet. Kann jemand erraten, wie? Ich gebe Ihnen einen Hinweis.
Angenommen, Alf und Ben bewegen sich wie üblich mit konstanter Geschwindigkeit auseinander. Alf sendet zwei Signale im Abstand $T$ aus, Ben reflektiert sie im Abstand $T^{\prime}$ und Alf empfängt sie im Abstand $T^{\prime\prime}$ wieder zurück. Wie kann Alf $K$ ausrechnen?
?

Antwort

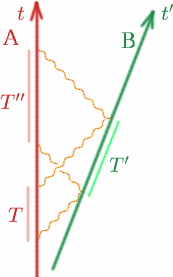
\begin{equation} {T^{\prime}} = {K T} \quad (9), \end{equation} \begin{equation} {T^{\prime\prime}} = {K T^{\prime}}\quad (10) \end{equation} Daher ist \begin{equation} {T^{\prime\prime}} = {K(K T)} = {K^2 T}\quad (11) \end{equation} also haben wir \begin{equation} {K} = {\sqrt{T^{\prime\prime}/T}}. \quad (12) \end{equation} Problem Um ein kompliziertes Andockmanöver durchführen zu können, ist es wichtig, dass zwei Raumfahrzeuge relativ zueinander in Ruhe gehalten werden. Entwickeln Sie ein einfaches Experiment, um dies zu überprüfen.

Der Zusammenhang zwischen K und Geschwindigkeit

Wir wissen bereits, dass, wenn die Relativgeschwindigkeit von Alf und Ben Null ist, $K$ = $1$ ist. Welchen Wert hat er für allgemeine Geschwindigkeiten? Es gibt einen cleveren Weg, dies herauszufinden, der die Idee, über die wir gerade gesprochen haben, plus die Idee der Gleichzeitigkeit verwendet. Was bedeutet das? Das erkläre ich gleich.
Stellen wir uns zunächst unsere üblichen zwei Beobachter vor, die sich mit konstanter Geschwindigkeit $v$ voneinander entfernen. Nehmen wir an, wenn sie zusammen sind, stellen beide ihre Uhren auf $t = 0$. Zum Zeitpunkt $T$ nach seiner Uhr sendet Alf ein Funksignal aus; Ben reflektiert es zum Zeitpunkt $T’$ nach seiner Uhr und Alf erhält es zum Zeitpunkt $T^{\prime\prime}$ nach seiner Uhr wieder zurück. Zeichnen wir wie üblich ein Bild.
?

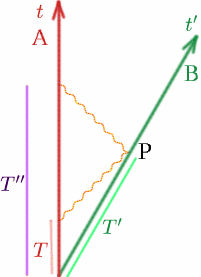
Nun wissen wir, dass \begin{equation} {T^{\prime}} = {K T}\quad (13) \end{equation} \begin{equation} {T^{\prime\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{equation} Alf denkt also, dass die Laufzeit des Funkimpulses \begin{equation} {T^{\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T} ist, \quad (15) \end{equation} und Alf rechnet aus, dass die Entfernung $D$ zwischen ihm und Ben die Hälfte der vom Funksignal zurückgelegten Strecke ist, also die Hälfte der Geschwindigkeit mal der Zeit: \begin{equation} {D} = {\frac {1} {2} c(K^2-1)T}. \quad (16) \end{equation} Nun wissen wir, dass sich der Abstand zwischen Alf und Ben ständig ändert, also müssen wir fragen, wann (d.h. zu welchem Zeitpunkt) dies der Abstand zwischen Alf und Ben ist. Hier brauchen wir die Idee der Gleichzeitigkeit. Die Entfernung wird eindeutig gemessen, wenn Ben sich am Punkt $P$ befindet, aber welcher Zeit entspricht dies für Alf? Nun, Alf weiß, dass der Funkimpuls die gleiche Strecke hin und zurück zurücklegt, so dass das Ereignis $Q$, das Alf als zur gleichen Zeit wie $P$ einschätzt, auf halbem Weg zwischen $T$ und $T^{\prime\prime}$ liegt. (Wir sagen, dass $Q$ für Alf gleichzeitig mit $P$ ist – das bedeutet einfach, dass es zur gleichen Zeit stattfindet.) Die Zeit bei $Q$ ist also \begin{equation} {T_Q} = {\frac {1} {2}(T+T“)} = {\frac {1} {2} (K^2+1)T}. \quad (17) \end{equation} Daraus schließt Alf, dass Ben in der Zeit $T_Q$ eine Strecke $D$ zurückgelegt hat, also ist seine Geschwindigkeit $v$ gegeben durch \begin{equation} {v} = {\frac {D} {T_Q}} = {\frac {\frac {1} {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \quad (18) \end{equation} Wir haben also \begin{equation} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \quad (19) \end{equation} Wir können nun $K$ in Bezug auf $\frac {v} {c}$ ausrechnen: \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Also \begin{equation} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}\quad (23) \end{equation} und somit \begin{equation} {K} = \sqrt{{\left({\frac{1+\frac{v}{c}}{1-\frac{v}{c}}\right)}}. \quad (24) \end{equation} Versuchen Sie, einige Werte von K auszurechnen:
z.B. $v = c/4$ – das ergibt $K = \sqrt{5/3} = 1.291$.
Nun versuchen Sie $v = c/2, 9c/10, 99c/100$.
Jetzt ist es egal, ob Alf stillsteht und Ben sich bewegt oder umgekehrt – $K$ ist immer noch gleich. Anders ist es, wenn Alf und Ben sich aufeinander zubewegen, anstatt sich auseinander zu bewegen – in diesem Fall nehmen wir den Wert von $v$ als negativ an, aber wir können die gleiche Formel verwenden.
Wenn Alf und Ben sich mit der relativen Geschwindigkeit $c/2$ aufeinander zubewegen, ist z.B. K = \sqrt{{\left({\frac{1+(-1/2)}{1-(-1/2)}}\right)}} = \sqrt{{\left({\frac{1/2}{3/2}}\right)}} = \sqrt{1/3}. \quad (25) \end{equation}. Berechnen wir $K$ für einige typische Geschwindigkeiten:
1) Verkehrsflugzeuge, die sich mit einer Geschwindigkeit von $1000km/h$ aufeinander zubewegen;
2) Galaxien in unserem Galaxienhaufen, die sich mit einer relativen Geschwindigkeit von $500km/s$ auseinander bewegen;
3) ein Auto, das sich mit $100km/h$ einem Polizisten nähert;
4) du gehst mit $5km/h$ auf deinen Freund zu$ Glaubst du, dass einer dieser Effekte beobachtbar wäre? Das Zwillingsparadoxon – endlich!
Was passiert? Warum ist es ein Paradoxon? (Was bedeutet das Wort Paradoxon überhaupt?)
Betrachten wir einmal eineiige Zwillinge, Albertina und Brigitta! Albertina bleibt zu Hause in London, während Brigitta, die Abenteuerlustige, auf eine Weltraumreise geht. Sie reist in einem sehr schnellen Raumschiff, das sich mit $v = 4c/5$ bewegt, 6 Jahre lang von der Erde weg, gemessen an ihrer Uhr. Dann kehrt sie mit der gleichen Geschwindigkeit für 6 Jahre zurück. Brigitta misst also eine Zeit von 12 Jahren für ihre Reise – sie ist 12 Jahre älter, wenn sie zu Albertina nach London zurückkehrt. Aber wie viel älter ist Albertina? Mal sehen, ob du mit deiner Vermutung richtig lagst oder vielleicht nur knapp daneben!
Zeichnen wir ein Raum-Zeit-Diagramm: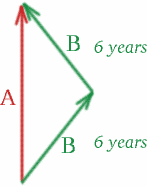
Auf Brigittas Hinreise bewegen sich die Zwillinge mit der Relativgeschwindigkeit $v = 4c/5$ auseinander, also \begin{equation} {K^2} = {\frac{1+\frac{4}{5}}{1-\frac{4}{5}}} = {9}, \quad (26) \end{equation} und wir haben $K=3$. Auf Brigittas Rückweg nähern sie sich einander mit der gleichen Geschwindigkeit, also \begin{equation} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}\quad (27) \end{equation} und $K=1/3$. Um die Zeit zu berechnen, die Albertina misst, müssen wir nur ein Lichtsignal einsetzen! Irgendwelche Vorschläge, wo?
Angenommen, Albertina sendet an dem Punkt $S$ ein Signal, das so gewählt ist, dass es Brigitta an $U$ erreicht, gerade als sie sich umdrehen will.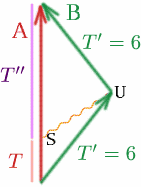
Was ist dann $T$, wenn $T^{\prime}=6$ und $K=3$? Wir haben \begin{equation} {T^{\prime}} = {K T} \quad (28) \end{equation}
also $6=3T$ und $T=2$.
Betrachten wir nun, was auf Brigittas Rückreise passiert. Wie groß ist $T^{\prime\prime}$? Wir haben $T^{\prime}=6$, $K=1/3$ und \begin{equation} {T^{\prime}} = {K T^{\prime\prime}}, \quad (29) \end{equation} also $6=T^{\prime\prime}/3$ und $T^{\prime\prime}=18$. Daher beträgt die von Albertina gemessene Gesamtzeit $T+T^{\prime\prime}=20$ Jahre, sie ist also 20 Jahre älter, wenn sie sich treffen, während Brigitta nur 12 Jahre älter ist! Albertina ist also um 8 Jahre mehr gealtert als Brigitta!
Hast du also richtig geraten????
Was du selbst versuchen kannst, sind einige Experimente mit Zahlen. Du kannst dir zum Beispiel vorstellen, dass Brigitta eine Reise von sagen wir $10+10=20$ Jahren macht, und du kannst ausrechnen, wie schnell sie reisen muss, damit Albertina nur um ein Jahr mehr gealtert ist als sie (d.h. $21$ Jahre sind auf Albertinas Uhr vergangen), wenn Brigitta zurückkommt. Vielleicht kannst du ausrechnen, ob es eine realistische (d.h. realisierbare) Weltraumreise geben kann, bei der die Zwillinge merklich unterschiedlich altern würden!
Warum nennt man das Ganze nun ein Paradoxon? Erinnern Sie sich, was Paradoxon bedeutet? Wir haben vorhin gesagt, dass, wenn sich zwei Menschen mit konstanter Geschwindigkeit (und damit mit konstanter Geschwindigkeit relativ zueinander) bewegen, vieles von dem, was passiert, dasselbe ist, egal ob wir den ersten als stationär und den zweiten als beweglich betrachten oder umgekehrt. Wenn wir dieses Argument auf Albertina und Brigitta anwenden, warum können wir dann nicht Brigitta in ihrem Raumschiff als die Person betrachten, die stillsitzt, und Albertina auf der Erde, die wegfliegt und dann zurückkommt. So ausgedrückt, klingt es etwas albern, aber ich hoffe, Sie verstehen die Idee. Dann würden wir erwarten, dass Brigitta älter ist als Albertina, wenn sie sich schließlich treffen. Wir haben aber schon gesagt, dass Albertina dann älter ist. Wie können diese beiden Aussagen wahr sein? Das ist das Paradoxon!
Siehst du, was falsch ist?
Der Punkt ist, dass Brigitta sich nicht mit konstanter Geschwindigkeit in Bezug auf Albertina während ihrer gesamten Reise bewegt; sie hat zwei lange Reiseabschnitte, in denen sie das tut, aber dazwischen gibt es einen möglicherweise kurzen, aber sehr wichtigen Abschnitt, in dem sie abbremst, anhält und dann in die entgegengesetzte Richtung beschleunigt. Die Beschleunigung ist ein echtes Phänomen, wie Sie wahrscheinlich von den Fahrgeschäften wissen, bei denen Ihnen auf dem Jahrmarkt schlecht wird! Wisst ihr, wie man das mit einem einfachen Gerät feststellen kann?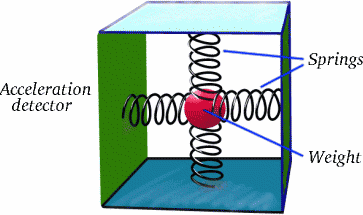
Was halten Sie nun von all dem? Es scheint ein bisschen ungerecht zu sein, dass Brigitta reisen und mehr vom Universum sehen darf, aber am Ende jünger ist als ihre zu Hause gebliebene Zwillingsschwester – das Leben scheint nicht immer fair zu sein! Aber es sollte dich ermutigen, zu reisen – nicht unbedingt ins Weltall! – und abenteuerlustig zu sein! Referenz Für weitere Diskussionen über das Zwillingsparadoxon und die hier beschriebenen Techniken können Sie versuchen, das Buch Flat and Curved Space-Times von G. F. R. Ellis und mir zu lesen (veröffentlicht von Oxford University Press im Jahr 1988). Sie könnten sich auch die Bücher von Mr. Tompkins ansehen, in denen die Konzepte der Speziellen Relativitätstheorie auf amüsante und verständliche Weise vorgestellt werden.

Auf der Website der Cambridge University Press finden Sie Rezensionen der Bücher von Mr. Tompkins und können sie bestellen, zum Beispiel unter The New World of Mr. Tompkins : George Gamow’s Classic Mr. Tompkinsin Paperback