Úvod

Pokud budete tento projekt sledovat, dovede vás k úžasnému závěru! Předpokládejme, že se jedno z dvojice jednovaječných dvojčat vydá na cestu do vesmíru a poté se vrátí a porovná svůj (řekněme svůj) věk s věkem druhého dvojčete, které zůstalo na stejném místě na Zemi. Ukáže se, že po cestě bude jedno dvojče mladší než jeho sestra! Jistě se ptáte, jak je tomožné, a cílem tohoto projektu je ukázat vám, jak.
Začneme tím, že si zahrajeme tipovací hru – na konci zjistíme, zda jste měli pravdu! Předpokládejme, že cestující dvojče se vydá na dvanáctiletou cestu – 6 let ven a 6 let zpět. Je zřejmé, že po návratu bude o 12 let starší. Vaším úkolem je odhadnout, o kolik bude starší dvojče, které necestuje….! Musím vám říct, jak rychle cestuje pohybující se dvojče – řekněme čtyři pětiny rychlosti světla – i když si troufám tvrdit, že vám to s odhadem příliš nepomůže! Dovolte mi, abych vám doporučil odhadnout celé číslo mezi 1 a 30!“
Než se budeme zabývat dvojčaty, musíme si připravit určité nástroje, které budeme potřebovat, abychom pochopili, o co jde. Budeme hojně využívat určitý druh grafu, který se nazývá časoprostorový diagram. Nebojte se, pokud jste ještě nikdy grafy nepoužívali – pokusíme se začít od základů.
?

Grafy

Nejjednodušší druh grafu je pouhý obrázek toho, co se děje na zvolené rovné ploše. Předpokládejme, že sedíte u stolu nebo psacího stolu a že máte dvě pravítka a velký list papíru. Začněte v levém dolním rohu a umístěte jedno pravítko podél spodní a druhé nahoru po levé straně, přičemž papír bude umístěn mezi nimi. To, co máte, by mělo vypadat takto:

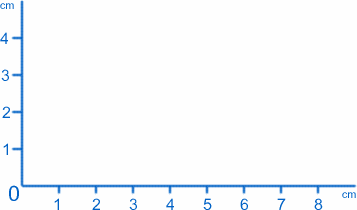
Bod, kde se obě pravítka setkávají (nula na obou stupnicích), budeme nazývat počátek nebo zkráceně O a pravítka nám poskytnou dvě osy . Podle konvence budeme tu podél spodní části nazývat osou x a tu nahoře po straně osou y. Libovolný bod na papíře můžeme označit hodnotami $x$ a $y$, například počátek má $x=0$, $y=0$. Bod vzdálený 1 cm$ od osy y a 2 cm$ od osy x má hodnoty $x=1$, $y=2$ (opravdu to mám správně!).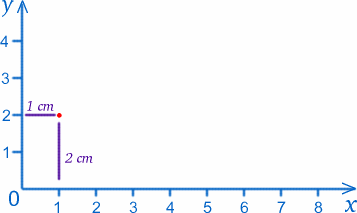

Cvičení Nakresli vlastní graf a vyznač následující body:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Jaký tvar tvoří?“
Teď si představ nějaké mravence s velmi špinavýma nohama. Předpokládejme, že jeden z nich chodí po papíře a zůstává vždy ve vzdálenosti $1cm$ od osy x. Jeho dráha by byla přímka popsaná rovnicí $y=1$ (efektní způsob, jak říci slovy to, co je řečeno v předchozí větě). Jiný by mohl jít vždy 3 cm$ od osy y; rovnice jeho cesty by byla $x=3$. Poněkud originálnější mravenec by mohl chodit tak, abyjeho vzdálenost od obou os byla vždy stejná; prošel by $x=1$, $y=1$; $x=2$, $y=2$; atd. a jeho dráha by byla dána rovnicí $x=y$.

Prostoročasové diagramy

V této části nakreslíme několik grafů, které vypadají velmi podobně jako v předchozí části, ale jejich význam bude poněkud jiný. Stále máme dvě osy a ta označená $x$ stále představuje vzdálenost v určitém směru. Ta, která byla označena $y$, je však nyní označena $t$, což představuje čas měřený řekněme v sekundách.Představme si například kuličku v pevném bodě vzdáleném 3 cm$ od bodu O; její dráha v časoprostoru bude přímka $x=3$. Nyní předpokládejme, že se kulička kutálí po přímé dráze; pak by body na grafu odpovídaly polohám kuličky v určitých časech, např. $x=5$, $t=4$ by odpovídaly tomu, že se kulička nachází 5cm$ od počátku $4$ sekundy po začátku měření času.
Cvičení Vyznačte na grafu body odpovídající následujícím událostem v historii kuličky: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Jak byste to interpretovali?
Nyní zkuste $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Čeho si na těchto bodech všimnete?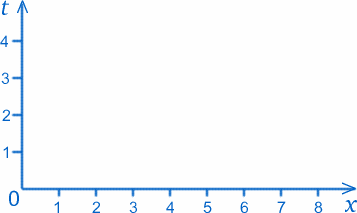
Pokud je dráha kuličky na grafu přímka, znamená to, že se kulička pohybuje konstantní rychlostí (třeba rychlostí nula). V takovém případě můžeme rychlost zjistit tak, že se podíváme, jakou vzdálenost urazí míček za jednu sekundu – změnu hodnoty x vydělíme příslušnou změnou hodnoty t. V takovém případě můžeme rychlost určit tak, že se podíváme, jakou vzdálenost urazí míček za jednu sekundu. V našem druhém příkladu je tedy rychlost míče $2cm/sec$. Souhlasíte s tím?“
Cvičení Nakreslete graf znázorňující pohyb míče, který se pohybuje dopředu a dozadu mezi dvěma body konstantní rychlostí (ale samozřejmě periodicky mění směr).
S naším grafem nyní provedeme něco poněkud zvláštního. V teorii zvané speciální teorie relativity , díky níž je zajímavé přemýšlet o dvojčatech a cestování vesmírem, musíme často do našich grafů zakreslovat světelné paprsky. Nyní se světelné paprsky pohybují v prázdném prostoru konstantní a velmi velkou (ale konečnou) rychlostí; světelný paprsek, který k vám dorazí zeSlunce, jej opustil asi před $8$ minutami. (Lidé dříve věřili, že světlo se pohybuje nekonečně rychle, takže hvězdy vidíte v okamžiku, kdy je pozorujete, ale dnes je známo, že to není pravda.) Přesněji řečeno, rychlost světla je asi $30000000000cm/sec$! To by mohlo vést k velmi podivným měřítkům na osách časoprostorového grafu, takže se rozhodneme měřit vzdálenost jiným způsobem; jednotkami na ose x budou světelné sekundy, tedy vzdálenost, kterou světlo urazí za jednu sekundu. (Je-li měřítkem pro $t$ rok, bude odpovídajícím měřítkem x světelný rok.)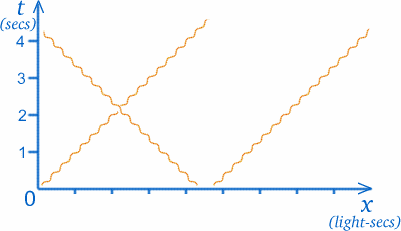
Velkou výhodou tohoto postupu je, že dráha světelného paprsku bude vždy v úhlu $45$ stupňů k osám. To znamená, že světelný paprsek procházející bodem O bude svírat s oběma osami stejné úhly, jak vidíte na obrázku. (Přestože se světlo pohybuje konstantní rychlostí, takže jeho dráha je přímka, znázorňujeme ji klikatou čarou, jak je znázorněno na obrázku, abychom odlišili dráhy světelných paprsků od drah jiných objektů s hmotností.)
?

Měření času

Máme tendenci předpokládat, že když se lidé neshodnou na tom, kolik je hodin, něčí hodinky jsou špatně, nebo jsou možná lidé v různých časových pásmech! Ale je to ještě složitější! Podle speciální teorie relativity mohou být dva lidé na stejném místě a korelovat své hodinky, ale pokud se jeden vůči druhému pohybuje, následně se neshodnou na tom, kolik je hodin. bohužel pokud se spojíte s kamarádem a pokusíte se tuto teorii otestovat, budete zklamáni, ne proto, že by teorie byla špatná, ale proto, že při rychlosti, kterou pravděpodobně dokážete běžet, i když jste superatlet, bude efekt příliš malý na to, abyste ho mohli pozorovat. Teprve když se rychlost stane velmi velkou (značný zlomek rychlosti světla), lze tento podivný jev pozorovat, a i tehdy pouze za použití extrémně přesných hodin.
Abychom viděli, jak by to mohlo fungovat, uvažujme o „myšlenkovém experimentu“ podobném tomu, který navrhl Einstein. (Je to spíše „myšlenkový“ než skutečný experiment, protože ho ve skutečnosti nelze provést, jak si jistě uvědomujete.) Předpokládejme, že sledujete hodiny na Big Benu velmi silným dalekohledem, zatímco se od něj vzdalujete velmi rychlým vlakem, který hodiny míjí přesně v poledne (vím, že vlaky nejezdí přímo kolem Big Benu, ale předstírejme to!). Kdyby se vlak pohyboval rychlostí světla, co byste viděli, že se děje s ručičkami hodin? Zdálo by se, že stojí na místě a obě ukazují na 12 dolarů! Proč? Je to proto, že světlo vyzařované ručičkami (nebo odražené od nich) v poledne by se od hodin vzdalovalo přesně stejnou rychlostí jako vy ve vlaku a světlo vyzařované v pozdějším čase by nemohlo vlak dohnat! Divné!
Víte, proč se jedná o „myšlenkový experiment“ (kromě toho, že vlaky kolem Big Benu nejezdí)? Je to proto, že vlak by se ve skutečnosti nemohl pohybovat rychlostí světla (což je něco jiného, co nám říká speciální teorie relativity – žádný objekt, který něco váží, se nikdy nemůže pohybovat tak rychle jako světlo). Předpokládejme však, že by se vlak pohyboval poloviční rychlostí světla (stále velmi rychle) – viděli byste, že se hodinové ručičky pohybují, ale pomaleji než ty na vašich hodinkách! Měření času závisí na tom, jak se pohybujete!
Jak je to možné? Abychom to pochopili, uvažujme zvláštní druh hodin, světelné hodiny . Není pravděpodobné, že byste takové hodiny našli vedle své postele, která vás ráno budí. Skládají se ze zdroje světla, který vysílá signály, jež urazí vzdálenost D a pak se odrazí zpět ke zdroji. Časová mezera nebo interval mezi každým vysláním signálu a jeho zpětným přijetím definuje tikání hodin; k nim dochází s časovým odstupem $2T$, kde \begin{rovnice} {T} = {D/c} \konec {rovnice}, přičemž $c$ představuje rychlost světla. (Nezapomeňte, že rychlost = vzdálenost/čas, takže čas = vzdálenost/rychlost.)

Předpokládejme nyní, že takové hodiny nese pohybující se raketa – podle zkušenosti posádky budou tikat v intervalech $2T$. Nyní předpokládejme, že posádka nehybné rakety pozoruje hodiny té pohybující se a porovnává je se svými vlastními, které také tikají v intervalech $2T$. Co uvidí? Odpověď by měly naznačit níže uvedené diagramy. (Omlouvám se, že mé rakety vypadají spíše jako ryby!)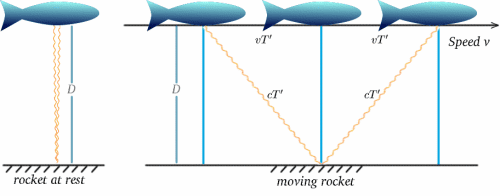
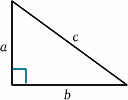
U pohybující se rakety se světlo odráží od zrcadla v polovině doby mezi vysláním signálu a jeho odrazem zpět. Ze stojící rakety se zdá, že doba cesty je $2T^{ \prime}$ řekněme. Můžeme to vypočítat pomocí velmi důležité věty (módní název pro něco, co bylo v matematice dokázáno jako pravdivé!) – Pythagorovy věty.

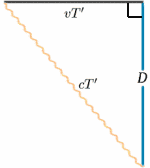\begin{rovnice} {a^2 + b^2} = {c^2} \quad (1) \end{rovnice} V raketovém diagramu máme pravoúhlý trojúhelník, takže \begin{rovnice} D^2 + v^2 T^{‚2} = {c^2 T ^{\prime 2}}\quad (2) \end{equation} Nyní to vyřešíme pro $T^{\prime}$: \begin{rovnice} {T^{\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{rovnice} \begin{rovnice} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{rovnice} dává \begin{rovnice} {T^{\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}} \quad (5) \end{equation} a tak \begin{equation} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}}, \quad (6) \end{equation} a taktovací frekvence budou různé (pokud samozřejmě $v=0$). Ve skutečnosti je $T^{\prime}$ větší než $T$, takže pro stacionární posádku to vypadá, jako by pohybující se hodiny měly delšíintervaly mezi tiky, a proto jdou pomalu.
Pokud přijmeme, že neexistuje univerzální definice času, která by platila pro všechny, musíme se zamyslet, co vlastně myslíme měřením času. V jistém smyslu měříme vzdálenosti podél našich drah v časoprostoru (vzpomeňte si na časoprostorový diagram). Dvojčata se pohybují po různých cestách v časoprostoru, takže není tak překvapivé, že prožilarozdílné množství času.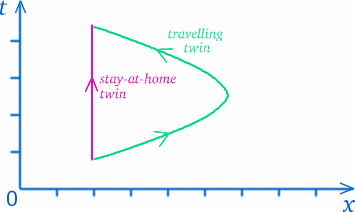
Ale nedělejte ukvapené závěry – věci nejsou vždy takové, jaké se zdají být…! Dráha cestujícího dvojčete vypadá delší, ale znamená to, že zažila více času? Abychom si uvědomili, jak je tento druh otázek záludný, zamysleme se nad situací, která může být dosti podobná. Předpokládejme, že bydlíte v Trumpingtonu na jižní straně Cambridge a chcete jít nakoupit do Tesca na severním okraji centra města (pokud možno tak, abyste se vyhnuli pěším zónám), na okružní silnici nebo na obchvat – viz schéma níže.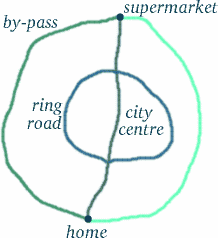
Ve většině denních dob byste zjistili, že nejdelší trasa – obchvat – zabere nejméně času, následovaná okružní silnicí.
Jste nyní přesvědčeni, že zřejmá odpověď není vždy správná?“
Viděli jsme, jak se měří čas pomocí světelných signálů. Jakmile budeme mít přesné hodiny, můžeme pak měřit vzdálenost pomocí světelných nebo radarových signálů odražených od vzdáleného objektu; vzdálenost bude polovina doby cesty světla vynásobená rychlostí světla.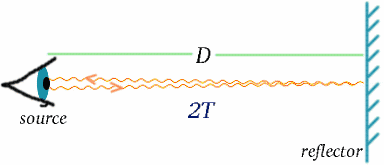

\begin{rovnice} {D} = {cT}\quad (7) \end{rovnice} Stejně jako čas je i vzdálenost veličinou, u níž výsledek měření závisí na způsobu, jakým se pozorovatel pohybuje.

K-faktory

Nyní popíšu myšlenku, která by nám měla pomoci při výpočtech typu efektu, o kterém jsem vám vyprávěl.
Předpokládejme, že astronaut B (pro Ben) se v raketě pohybuje rychlostí $c/5$ od jiného astronauta A (pro Alf) na vesmírné stanici. Jednou ročně 13. března Alf posílá Benovi blahopřání k narozeninám. Předpokládejme, že rádiová zpráva nesoucí tento pozdrav v roce 2010 podle měření vesmírné stanice urazí vzdálenost půl světelného roku, než dorazí k raketě, a trvá jí to půl roku. Dalšízpráva je odeslána přesně o rok později. Když tento rádiový signál urazí půl roku do místa, kde astronaut Ben přijal předchozí signál, raketa se posunula o pětinu světelného roku dál, takže tento signál musí urazit delší cestu, aby raketu dohnal; ve skutečnosti je čas měřený Alfem, kdy signál dorazí k raketě, tři čtvrtě roku po jeho vyslání – viz diagram níže. Chudák Alf dospěl k závěru, že podle Alfových hodin bude Ben každoročně zasílaná blahopřání k narozeninám přijímat v intervalu jednoho a čtvrt roku.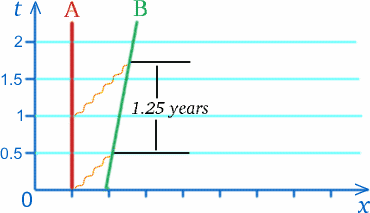
To nám sice neříká, kolik bude Ben měřit za tyto intervaly, ale naznačuje to, že to dost možná nebude rok! Podobný efekt nastane i u signálů vysílaných od Bena k Alfovi.
Nyní se podívejme na obecný případ a upřesněme si to. Uvažujme dva pozorovatele Alfa a Bena, kteří se od sebe vzdalují konstantní rychlostí.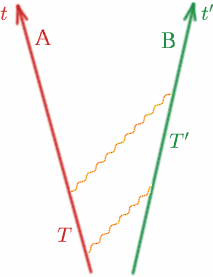
Alf vyšle světelný signál a pak další v čase $T$ později. Ben tyto dva signály přijme s časovým odstupem $T^{\prime}$ podle svých hodin. Pak definujeme veličinu $K$ vztahem \begin{rovnice} {K} = {T^{\prime}/T}. \kvadrát (8) \konec{rovnice} Všimněte si, že kdyby se Alf a Ben pohybovali stejnou rychlostí (stejným směrem!), bylo by $K$ rovno jedné. Přesněji uvidíme, jak $K$ závisí na relativní rychlosti Alfa a Bena. $K$ se někdy nazývá faktor Dopplerova posunu a efekt je podobný jako u zvukových vln – všichni jistě znáte změnu zvuku sirény sanitky nebo policejního auta, když se blíží a pak vzdaluje.
Jak můžeme změřit $K$? Zřejmým způsobem je, že si pozorovatelé vedou záznamy o tom, kdy jsou světelné signály vysílány a přijímány, aby mohli zjistit $T$ a $T^{\prime}$, a tedy i $K$, až se později setkají. Další možností by bylo, kdyby jeden z nich měl velmi výkonný dalekohled, kterým by sledoval hodiny toho druhého (to je vlastně zase ten vlak jedoucí kolem Big Benu!).
Abychom mohli toto číslo použít, musíme o něm učinit určité předpoklady $K$. Nejprve předpokládáme, že když se Alf a Ben pohybují konstantní rychlostí, pak $K$ nezávisí na tom, kdy měříme $T$ a $T^{\prime}$, ani na tom, jak velké je $T$. Pokud tedy například Alf čeká mezi vysláním světelných signálů dvakrát déle, $K$ bude stejné. Zkuste, zda v tomto případě dokážete doplnit čísla $T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$.
?

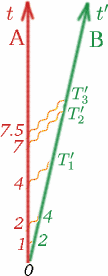
(Všimněte si, že je v pořádku začít měřit čas, když jsou oba pozorovatelé spolu, a oba mohou v tomto okamžiku nastavit své stopky na nulu.) Obecně tedy máme
?

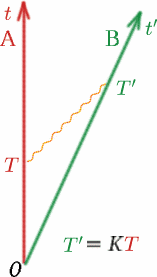
Druhou věcí, kterou předpokládáme a která je stejně důležitá, je, že $K$ naměřený Benem pro světelné signály od Alfa je stejný jako ten, který naměřil Alf pro světelné signály od Bena. Proč to předpokládáme? Představte si dvě stejná auta za sebou na silnici. Auto $A$ zůstane stát a auto $B$ se rozjede rychlostí $50km/h$ od auta $A$. Cestující, kteří se dívají zadním okénkem auta $A$, uvidí, že $B$ mizí odpovídající rychlostí. Cestující ve voze $B$ uvidí velmi podobný obraz, pokud se budou dívat zadním oknem – bude se jim zdát, že se vůz $A$ vzdaluje stejnou rychlostí! Už se vám někdy stalo, že jste seděli ve vlaku a mysleli si, že se právě rozjel, když se ukázalo, že to byl sousední vlak, který se rozjel opačným směrem a váš vlak stále stojí?
Tento předpoklad umožňuje, aby jeden pozorovatel změřil $K$ radarem bez jakékoliv spolupráce s druhým. Dokáže někdo odhadnout jak? Napovím vám.
Předpokládejme jako obvykle, že Alf a Ben se pohybují od sebe konstantní rychlostí. Alf vyšle dva signály v intervalu $T$, Ben je odrazí v intervalu $T^{\prime}$ a Alf je přijme zpět opět v intervalu $T^{\prime\prime}$. Jak může Alf zjistit $K$?
?

Odpověď

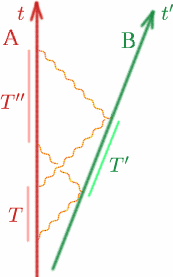
\begin{rovnice} {T^{\prime}} = {K T} \quad (9), \end{rovnice} \begin{rovnice} {T^{\prime\prime}} = {K T^{\prime}}\quad (10) \end{rovnice} Proto \begin{rovnice} {T^{\prime\prime}} = {K(K T)} = {K^2 T}\quad (11) \end{rovnice} takže máme \begin{rovnice} {K} = {\sqrt{T^{\prime\prime}/T}}. \quad (12) \end{rovnice} Problém Pro provedení složitého dokovacího manévru je nezbytné, aby dvě kosmické lodě byly vůči sobě v klidu. Vymyslete jednoduchý experiment, kterým ověříte, že tomu tak je.

Závislost mezi K a rychlostí

Již víme, že pokud je relativní rychlost Alf a Ben nulová, pak $K$ = $1$. Jaká je její hodnota pro obecné rychlosti? Existuje chytrý způsob, jak to vyřešit, který využívá myšlenku, o níž jsme právě hovořili, a navíc myšlenku simultánnosti. Co to znamená? Vysvětlím to za chvíli.
Nejprve si představme naše dva obvyklé pozorovatele, kteří se od sebe vzdalují konstantní rychlostí $v$. Předpokládejme, že když jsou spolu, oba nastaví své hodiny na hodnotu $t = 0$. V čase $T$ podle svých hodin Alf vyšle rádiový signál; Ben jej odrazí zpět v čase $T’$ podle svých hodin a Alf jej dostane zpět opět v čase $T^{\prime\prime}$ podle svých hodin. Nakresleme si obrázek jako obvykle.
?

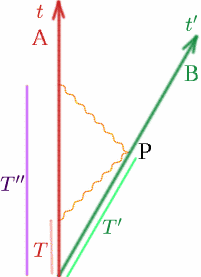
Nyní víme, že \begin{rovnice} {T^{\prime}} = {K T}\quad (13) \end{rovnice} \begin{rovnice} {T^{\prime\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{rovnice} Alf si tedy myslí, že doba cesty rádiového impulsu je \begin{rovnice} {T^{\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{rovnice} a Alf zjistí, že vzdálenost $D$ mezi ním a Benem je polovina vzdálenosti, kterou urazil rádiový signál, což je polovina rychlosti krát čas: \begin{rovnice} {D} = {\frac {1} {2} c(K^2-1)T}. \quad (16) \end{rovnice} Nyní víme, že vzdálenost mezi Alfem a Benem se neustále mění, takže se musíme ptát, kdy (tj. v jakém čase) je tato vzdálenost mezi Alfem a Benem. Zde se nám hodí myšlenka simultánnosti. Vzdálenost je jasně měřena, když je Ben v bodě $P$, ale jakému času to odpovídá pro Alfa? Alf ví, že rádiový impuls urazí stejnou vzdálenost ven i zpět, takže událost $Q$, o níž Alf usoudí, že nastane ve stejný čas jako $P$, bude v polovině cesty mezi $T$ a $T^{\prime\prime}$. (Říkáme, že událost $Q$ je pro Alfa současná s událostí $P$ – znamená to prostě ve stejnou dobu.) Takže čas v $Q$ je \begin{rovnice} {T_Q} = {\frac {1} {2}(T+T“)} = {\frac {1} {2} (K^2+1)T}. \quad (17) \end{rovnice} Alf tedy dospěl k závěru, že Ben urazil vzdálenost $D$ za čas $T_Q$, takže jeho rychlost $v$ je dána vztahem \begin{rovnice} {v} = {\frac {D} {T_Q}} = {\frac {\frac {1} {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \quad (18) \end{rovnice} Máme tedy \begin{rovnice} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \quad (19) \end{rovnice} Nyní můžeme vypočítat $K$ v termínech $\frac {v} {c}$: \begin{rovnice} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{rovnice} \begin{rovnice} {K^2 \frac{v}{c} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{equation} \begin{rovnice} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{rovnice} Proto \begin{rovnice} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}}\quad (23) \end{equation} a tedy \begin{equation} {K} = \sqrt{{\left({\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}\right)}}. \quad (24) \end{rovnice} Zkuste vypočítat některé hodnoty K:
např. $v = c/4$ – to dává $K = \sqrt{5/3} = 1,291$.
Teď zkuste $v = c/2, 9c/10, 99c/100$.
Teď je jedno, jestli Alf stojí a Ben se pohybuje, nebo naopak – $K$ je stále stejné. Jiné je to, pokud se Alf a Ben k sobě přibližují, a ne se od sebe vzdalují – v takovém případě bereme hodnotu $v$ jako zápornou, ale můžeme použít stejný vzorec.
Např. pokud se Alf a Ben k sobě přibližují relativní rychlostí $c/2$, \begin{rovnice} K = \sqrt{{\levice({\frac{1+(-1/2)}{1-(-1/2)}}}\pravice)}}} = \sqrt{{{\levice({\frac{1/2}{3/2}}}\pravice)}} = \sqrt{1/3}. \quad (25) \end{rovnice}. Vypočítejme $K$ pro některé typické rychlosti:
1) letadla blížící se k sobě rychlostí 1000 km/hod$;
2) galaxie v naší kupě pohybující se od sebe relativní rychlostí 500 km/s$;
3) auto blížící se k policistovi rychlostí 100 km/hod$;
4) vy jdete ke svému kamarádovi rychlostí 5 km/hod$ Myslíte si, že některý z těchto efektů bude pozorovatelný? Paradox dvojčat – konečně!
Co se stane? Proč se jedná o paradox? (Co vlastně znamená slovo paradox?)
Uvažujme o jednovaječných dvojčatech Albertině a Brigitě! Albertina zůstává doma v Londýně, zatímco Brigitta, ta dobrodružná, se vydává na výlet do vesmíru. Vzdálí se od Země na 6 let, měřeno jejími hodinami, ve velmi rychlé vesmírné lodi, která se pohybuje rychlostí $v = 4c/5$. Poté se stejnou rychlostí po dobu 6 let vrací zpět. Brigitta tedy během své cesty změřila čas 12 let – když se vrátí domů k Albertině do Londýna, je o 12 let starší. O kolik je ale Albertina starší? Podívejme se, zda byl váš odhad správný, nebo zda byl jen těsný!
Nakresleme časoprostorový diagram: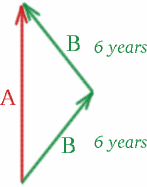
Na Brigittině cestě ven se dvojčata od sebe vzdalují relativní rychlostí $v = 4c/5$, takže \begin{rovnice} {K^2} = {\frac{1+\frac{4}{5}}{1-\frac{4}{5}}} = {9}, \quad (26) \end{rovnice} a máme $K=3$. Při zpáteční cestě Brigitty se k sobě přibližují stejnou rychlostí, takže \begin{rovnice} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}}}\quad (27) \end{rovnice} a $K=1/3$. Jediné, co musíme udělat, abychom zjistili čas, který Albertina měří, je vložit jeden světelný signál! Nějaké návrhy kam?
Předpokládejme, že Albertina vyšle signál v bodě $S$, který byl zvolen tak, aby dorazil k Brigitě v bodě $U$, právě když se chystá otočit.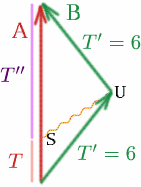
Jaká je tedy hodnota $T$, jestliže $T^{\prime}=6$ a $K=3$? Máme \begin{rovnice} {T^{\prime}} = {K T} \quad (28) \end{rovnice}
takže $6=3T$ a $T=2$.
Teď se podívejme, co se stane na zpáteční cestě Brigitty. Kolik je $T^{\prime\prime}$? Máme $T^{\prime}=6$, $K=1/3$ a \begin{rovnice} {T^{\prime}} = {K T^{\prime\prime}}, \quad (29) \end{rovnice} takže $6=T^{\prime\prime}/3$ a $T^{\prime\prime}=18$. Celkový čas měřený Albertinou je tedy $T+T^{\prime\prime}=20$ let, takže v době setkání je starší o 20 let, zatímco Brigitta je starší pouze o 12 let! Albertina tedy zestárla o 8 let více než Brigitta!
Takže jsi hádal správně????
Co můžeš zkusit udělat sám, je několik pokusů s čísly. Můžeš si například představit, že Brigitta se vydá na cestu trvající řekněme 10+10=20$ let, a můžeš zjistit, jak rychle musí cestovat, aby Albertina zestárla jen o jeden rok více než ona (tj. na Albertininých hodinách uběhlo 21$ let), až se Brigitta vrátí. Možná bys mohl zjistit, zda by bylo možné, aby existovala reálná (tj. dosažitelná) vesmírná cesta, při které by dvojčata zestárla o znatelný rozdíl!
Tak proč se tomu všemu říká paradox ? Vzpomeňte si, co znamená paradox? Již dříve jsme si řekli, že pokud se dva lidé pohybují konstantní rychlostí (a tedy konstantní rychlostí vůči sobě navzájem), spousta věcí se děje stejně, ať už považujeme prvního za nehybného a druhého za pohybujícího se, nebo naopak. Aplikujeme-li tento argument na Albertinu a Brigittu,proč bychom nemohli považovat Brigittu v její vesmírné lodi za osobu, která stojí na místě, a Albertinu na Zemi, která odplouvá a pak se vrací. Takto vyjádřeno to zní poněkud hloupě, ale doufám, že jste pochopili myšlenku. Pak bychom očekávali, že Brigitta bude starší než Albertina, až se konečně setkají. Ale už jsme si řekli, že Albertina je tehdy starší. Jak by mohla být obě tato tvrzení pravdivá? To je přece paradox!“
Vidíš, co je špatně?“
Jde o to, že Brigitta se vůči Albertině nepohybuje po celou dobu své cesty konstantní rychlostí; má dva dlouhé úseky cesty, v nichž tak činí, ale mezi nimi je možná krátký, ale velmi důležitý úsek, v němž zpomaluje, zastavuje a pak zrychluje opačným směrem. To je to, co dělá rozdíl!“ Zrychlení je skutečný fenomén, jak jistě víte z atrakcí, ze kterých se vám na pouti dělá špatně! Víte, jak by se dalo zjistit pomocí jednoduchého zařízení?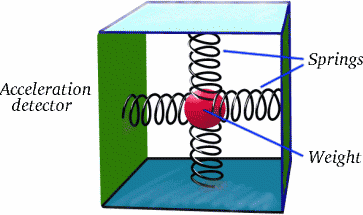
Tak co si o tom všem myslíte? Zdá se mi trochu nespravedlivé, že Brigitta může cestovat a vidět větší část vesmíru, ale nakonec je mladší než její dvojče, které zůstalo doma – život není vždycky spravedlivý! Ale mělo by vás to povzbudit k cestování – ne nutně ve vesmíru! – a být dobrodružný! Více informací o paradoxu dvojčat a zde popsaných technikách najdete v knize Flat and Curved Space-Times , kterou jsme napsali já a G. F. R. Ellis (vydalo nakladatelství Oxford University Press v roce 1988). Můžete se také podívat na knihy pana Tompkinse, které zábavnou a přístupnou formou představují koncepty speciální teorie relativity.

Na stránkách Cambridge University Press můžete najít recenze knih pana Tompkinse a objednat si je, například viz The New World of Mr Tompkins : George Gamow’s Classic Mr Tompkinsin Paperback

.