Introducere

Dacă veți urmări acest proiect, veți fi conduși la o concluzie uimitoare! Să presupunem că unul dintr-o pereche de gemeni identici pleacă într-o călătorie în spațiu și apoi se întoarce pentru a compara vârsta sa (să zicem a ei) cu cea a celuilalt geamăn care a rămas în același loc pe Pământ. Se pare că, după călătorie, una dintre gemene va fi mai tânără decât sora ei! Probabil că vă întrebați cum ar putea fi posibil acest lucru, iar scopul acestui proiect este de a vă arăta cum.
Să începem prin a juca un joc de ghicit – vom afla dacă ați avut dreptate la sfârșit! Să presupunem că geamănul călător pleacă într-o călătorie de 12 ani – 6 ani la plecare și 6 ani la întoarcere. Evident, ea va fi cu 12 ani mai mare când se va întoarce. Ceea ce trebuie să faci tu este să ghicești cât de mult va fi mai bătrân geamănul care nu călătorește….! Trebuie să vă spun cu cât de repede călătorește geamănul care se deplasează – să spunem patru cincimi din viteza luminii – deși îndrăznesc să spun că acest lucru nu vă va ajuta prea mult să ghiciți! Permiteți-mi să vă sugerez să ghiciți un număr întreg între 1 și 30!
Înainte de a lua în considerare gemenii, trebuie să stabilim anumite instrumente de care vom avea nevoie pentru a înțelege ce se întâmplă. Ne vom folosi foarte mult de un anumit tip de grafic numit diagrama spațiu-timp. Nu vă faceți griji dacă nu ați mai folosit grafice până acum – vom încerca să începem de la elementele de bază.
?

Grafuri

Cel mai simplu tip de grafic este doar o imagine a ceea ce se întâmplă pe o suprafață plană aleasă. Să presupunem că stați la o masă sau la un birou și că aveți două rigle și o bucată mare de hârtie. Începând de la colțul din stânga jos, așezați o riglă de-a lungul părții de jos și una în sus pe partea stângă, cu hârtia pe poziție între ele. Ceea ce aveți ar trebui să arate astfel:

Vom numi punctul în care se întâlnesc cele două rigle (zero pe ambele scări) originea, sau pe scurt O, iar riglele asigură cele două axe . Urmând convenția, o vom numi axa x pe cea de jos și axa y pe cea laterală. Putem eticheta orice punct de pe hârtie prin valorile lui $x$ și $y$. de exemplu, originea are $x=0$, $y=0$. Punctul aflat la $1cm$ de axa y și la $2cm$ de axa x are $x=1$, $y=2$ (chiar le am inversate corect!).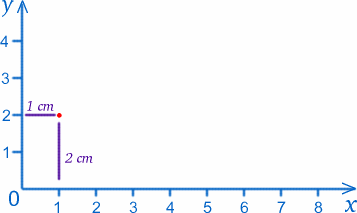

Exercițiu Desenează-ți propriul grafic și marchează următoarele puncte:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Ce formă formează ele?
Imaginează-ți acum niște furnici cu picioarele foarte murdare. Să presupunem că una dintre ele se plimbă pe hârtie rămânând mereu la o distanță de $1cm$ față de axa x. Traiectoria sa ar fi o linie, descrisă de ecuația $y=1$ (un mod fantezist de a spune ceea ce se spune în cuvinte în propoziția anterioară). Un altul ar putea merge întotdeauna la o distanță de $3cm$ față de axa y; ecuația traiectoriei sale ar fi $x=3$. O furnică ceva mai originală ar putea merge astfel încât distanța sa față de ambele axe să fie mereu aceeași; ar trece prin $x=1$, $y=1$; $x=2$, $y=2$; etc., iar traiectoria sa ar fi dată de ecuația $x=y$.

Diagrame spațio-temporale

În această secțiune, vom desena câteva grafice care arată foarte asemănător cu cele din secțiunea anterioară, dar semnificația lor va fi destul de diferită. Avem în continuare două axe, iar cea etichetată $x$ reprezintă în continuare distanța într-o anumită direcție. Cu toate acestea, cea care era etichetată $y$ este acum etichetată $t$, care reprezintă timpul, măsurat, de exemplu, în secunde.Imaginați-vă, de exemplu, o minge aflată într-un punct fix la 3 cm$ de O; traiectoria sa în spațiu-timp va fi linia dreaptă $x=3$. Acum să presupunem că bila se rostogolește de-a lungul unei traiectorii drepte; atunci punctele de pe grafic ar corespunde pozițiilor bilei la anumite momente, de exemplu $x=5$, $t=4$ ar corespunde faptului că bila se află la 5cm$ de origine la 4$ secunde după ce a început măsurarea timpului.
Exercițiu Trasați punctele de pe grafic care corespund următoarelor evenimente din istoria bilei: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Cum ați interpreta acest lucru?
Încercați acum $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. Ce observați la aceste puncte?
Dacă traiectoria bilei este o linie dreaptă pe grafic, înseamnă că bila se deplasează cu viteză constantă (poate viteza zero). În acest caz, putem calcula viteza văzând cât de departe parcurge bila într-o secundă – împărțim modificarea valorii x la modificarea corespunzătoare a valorii t. Așadar, în al doilea exemplu, viteza mingii este de 2 cm/sec$. Sunteți de acord?
Exercițiu Desenați un grafic care să reprezinte mișcarea unei bile care se deplasează înainte și înapoi între două puncte, cu viteză constantă (dar schimbându-și periodic direcția, bineînțeles).
Acum vom face ceva destul de ciudat cu graficul nostru. În teoria numită relativitate specială , care este ceea ce face să fie interesant să ne gândim la gemeni și la călătoriile în spațiu, deseori trebuie să reprezentăm razele de lumină pe graficele noastre. Acum, razele de lumină se deplasează în spațiul gol cu o viteză constantă și foarte mare (dar finită); o rază de lumină care ajunge la tine de la soare a plecat de acolo cu aproximativ $8$ minute în urmă. (Oamenii obișnuiau să creadă că lumina se deplasează infinit de repede, astfel încât puteai vedea stelele în momentul în care le observi, dar acum se știe că acest lucru este greșit). Pentru a fi mai precis, viteza luminii este de aproximativ $30000000000cm/sec$! Acest lucru ar putea duce la niște scări foarte ciudate pe axele unui grafic spațiu-timp, așa că vom alege să măsurăm distanța într-un mod diferit; unitățile de măsură de pe axa x vor fi secundele-lumină, adică distanța parcursă de lumină într-o secundă. (Dacă scara pentru $t$ este de ani, scara x corespunzătoare va fi de ani-lumină).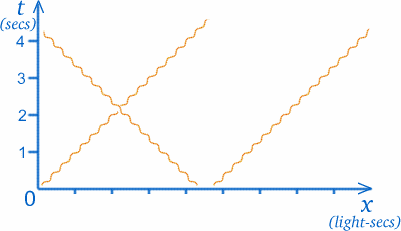
Marele avantaj al acestei metode este că traiectoria unei raze de lumină va fi întotdeauna la $45$ grade față de axe. Aceasta înseamnă că o rază de lumină care trece prin O va avea unghiuri egale față de ambele axe, așa cum se vede pe diagramă. (Deși lumina se deplasează cu viteză constantă, astfel încât traiectoria sa este o linie dreaptă, o reprezentăm printr-o linie ondulată, așa cum se arată, pentru a distinge razele de lumină de traiectoriile altor obiecte cu masă.)
?

Măsurarea timpului

Tindem să presupunem că atunci când oamenii nu sunt de acord cu privire la cât este ora, ceasul cuiva este greșit, sau poate că oamenii se află în fusuri orare diferite! Dar este chiar mai complicat decât atât! Conform relativității speciale, doi oameni se pot afla în același loc și își pot corela ceasurile, dar dacă unul dintre ei se deplasează în raport cu celălalt, ei vor fi ulterior în dezacord cu privire la cât este ceasul. din nefericire, dacă faceți echipă cu un prieten și încercați să testați această teorie, veți fi dezamăgiți, nu pentru că teoria este greșită, ci pentru că, la viteza cu care este probabil să puteți alerga, chiar dacă sunteți un super-atlet, efectul va fi prea mic pentru a fi observat. Doar atunci când vitezele devin foarte mari (fracțiuni considerabile din viteza luminii), acest fenomen ciudat poate fi observat și,chiar și atunci, doar prin utilizarea unor ceasuri extrem de precise.
Pentru a vedea cum ar putea funcționa acest lucru, să luăm în considerare un „experiment de gândire” similar cu cel pe care l-a sugerat Einstein. (Este mai degrabă un experiment „gândit” decât unul real, deoarece nu poate fi realizat în realitate, după cum vă veți da seama). Să presupunem că urmăriți ceasul de pe Big Ben printr-un telescop foarte puternic, în timp ce vă îndepărtați de el cu un tren foarte rapid care a trecut pe lângă ceas exact la prânz (știu că trenurile nu trec chiar pe lângă Big Ben, dar să ne prefacem!). Acum, dacă trenul s-ar putea deplasa cu viteza luminii, ce s-ar întâmpla cu acele ceasului? Ar părea că stau nemișcate, ambele arătând spre $12$! De ce? Pentru că lumina emisă de (sau reflectată de) mâini la prânz s-ar îndepărta de ceas cu exact aceeași viteză ca și tine în tren, iar lumina emisă mai târziu nu ar putea ajunge din urmă trenul! Ciudat!
Înțelegeți de ce acesta este un „experiment de gândire” (în afară de faptul că trenurile nu trec pe lângă Big Ben)? Este pentru că un tren nu s-ar putea mișca efectiv cu viteza luminii (ceea ce este un alt lucru pe care relativitatea specială ni-l spune – orice obiect care cântărește ceva nu se poate mișca niciodată la fel de repede ca lumina). Dar să presupunem că trenul se deplasează cu jumătate din viteza luminii (încă foarte rapid) – ați vedea cum se mișcă acele ceasului, dar mai încet decât cele de la ceasul dumneavoastră! Măsurarea timpului depinde de modul în care vă deplasați!
Cum se poate întâmpla acest lucru? Pentru a înțelege acest lucru, să luăm în considerare un tip special de ceas, un ceas de lumină . Este puțin probabil să găsiți unul dintre acestea lângă patul dumneavoastră care să vă trezească dimineața. Acesta constă într-o sursă de lumină care emite semnale care parcurg o distanță D și sunt apoi reflectate înapoi la sursă. Diferența de timp sau intervalul dintre fiecare dată când un semnal este emis și momentul în care este recepționat înapoi definește ticurile ceasului; acestea au loc la un interval de timp de $2T$, unde \begin{equation} {T} = {D/c} \end{equation} cu $c$ reprezentând viteza luminii. (Amintiți-vă că viteza = distanță/timp, deci timpul = distanță/viteză.)

Să presupunem acum că o rachetă în mișcare poartă un astfel de ceas – experiența echipajului va fi că ticăiturile se produc la intervale de $2T$. Să presupunem acum că echipajul unei rachete staționare observă ceasul rachetei în mișcare și îl compară cu al lor, care, de asemenea, ticăie la intervale de $2T$. Ce vor vedea ei? Diagramele de mai jos ar trebui să sugereze răspunsul. (Îmi pare rău că rachetele mele arată mai degrabă ca niște pești!)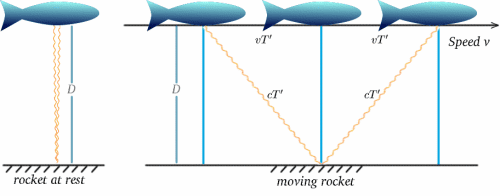
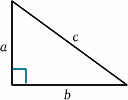
Pentru racheta în mișcare, lumina este reflectată de oglindă la jumătatea timpului dintre momentul în care semnalul este trimis și cel în care este reflectat înapoi. De la racheta staționară, timpul de parcurs pare a fi de $2T^{ \prime}$ să zicem. Putem calcula acest lucru folosind o teoremă foarte importantă (un nume fantezist pentru ceva ce s-a dovedit a fi adevărat în matematică!) – cea a lui Pitagora.

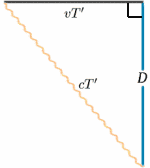\begin{equation} {a^2 + b^2} = {c^2} \quad (1) \end{equation} În diagrama rachetei, avem un triunghi dreptunghic, deci \begin{equation} D^2 + v^2 T^{‘2} = {c^2 T ^{\prime 2}}\quad (2) \end{equation} \end{equation} Rezolvăm acum această problemă pentru $T^{\prime}$: \begin{equation} {T^{{\prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \begin{equation} {T^{{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{equation} dând \begin{equation} {T^{\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}}\quad (5) \end{equation} și astfel \begin{equation} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}}, \quad (6) \end{equation} și ratele ceasurilor vor fi diferite (cu excepția cazului în care, desigur, $v=0$). De fapt, $T^{\prime}$ este mai mare decât $T$, astfel încât echipajului staționar i se pare că ceasul în mișcare are intervale mai lungi între ticuri și deci merge mai încet.
După ce acceptăm că nu există o definiție universală a timpului care să fie valabilă pentru toată lumea, trebuie să ne gândim la ce înțelegem cu adevărat prin măsurarea timpului. Într-un anumit sens, măsurăm distanțe de-a lungul drumurilor noastre în spațiu-timp (gândiți-vă la diagrama spațiu-timp). Gemenii urmează trasee diferite în spațiu-timp, așa că nu este atât de surprinzător faptul că au experimentat cantități diferite de timp.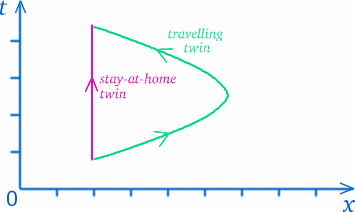
Dar nu trageți concluzii pripite – lucrurile nu sunt întotdeauna ceea ce par a fi…! Traiectoria geamănului călător pare mai lungă, dar înseamnă asta că ea a experimentat mai mult timp? Pentru a vedea cât de complicat este acest tip de întrebare, gândiți-vă la o situație care ar putea fi destul de asemănătoare. Să presupunem că locuiți în Trumpington, în partea de sud a orașului Cambridge, și doriți să mergeți la cumpărături la Tesco’s în extremitatea nordică a centrului orașului (pe cât de mult puteți, evitând zonele pietonale), pe șoseaua de centură sau pe varianta de ocolire – a se vedea diagrama de mai jos.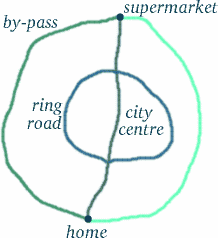
În majoritatea momentelor din zi, veți constata că traseul cel mai lung – by-pass-ul – durează cel mai puțin, urmat de șoseaua de centură. V-ați convins acum că răspunsul evident nu este întotdeauna cel corect?”
Am văzut cum se măsoară timpul cu ajutorul semnalelor luminoase. Odată ce avem un ceas precis, putem măsura distanța folosind semnale luminoase sau semnale radar reflectate de obiectul îndepărtat; distanța va fi jumătate din timpul de deplasare a luminii, înmulțit cu viteza luminii.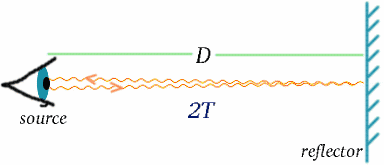

începem{echipă} {D} = {cT}\quad (7) \end{equation} Ca și timpul, distanța este o mărime în care rezultatul măsurătorii depinde de direcția în care se deplasează observatorul.

Factori K

Voi descrie acum o idee care ar trebui să ne ajute să facem calcule de tipul efectului despre care v-am vorbit.
Să presupunem că un astronaut B (pentru Ben) se află într-o rachetă care se deplasează cu viteza $c/5$ departe de un alt astronaut A (pentru Alf) aflat într-o stație spațială. O dată pe an, pe 13 martie, Alf îi trimite lui Ben felicitări de ziua lui Ben. Să presupunem că mesajul radio care transmite această urare în anul 2010 este măsurat de către stația spațială ca parcurgând o distanță de o jumătate de an-lumină pentru a ajunge la rachetă, având nevoie de o jumătate de an pentru a face acest lucru. Următorul mesaj este trimis exact un an mai târziu. Când acest semnal radio a parcurs jumătate de an până la locul unde Ben a primit semnalul anterior, racheta s-a deplasat cu o cincime de an-lumină mai departe, astfel încât acest semnal trebuie să călătorească mai mult timp pentru a ajunge la rachetă; de fapt, timpul măsurat de Alf când semnalul ajunge la rachetă este de trei sferturi de an după ce a fost trimis – vezi diagrama de mai jos. Bietul Alf concluzionează că felicitările de ziua de naștere trimise anual vor fi primite de Ben la intervale de un an și un sfert, conform ceasului lui Alf.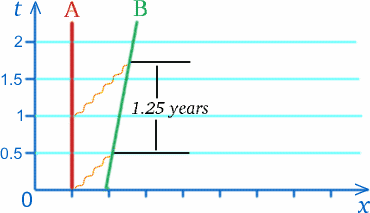
Aceasta nu ne spune ce va măsura Ben pentru aceste intervale, dar sugerează că s-ar putea foarte bine să nu fie un an! Un efect similar se va întâmpla pentru semnalele trimise de Ben către Alf.
Acum să ne uităm la cazul general și să facem acest lucru mai precis. Să considerăm doi observatori Alf și Ben care se îndepărtează unul de celălalt cu viteze constante.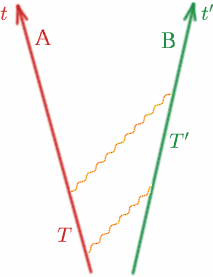
Alf trimite un semnal luminos și apoi un altul la un timp $T$ mai târziu. Ben primește cele două semnale la un interval de timp $T^{\prime}$, conform ceasului său. Atunci definim o cantitate $K$ prin \begin{equation} {K} = {T^{\prime}/T}. \quadru (8) \end{equation} Rețineți că, dacă Alf și Ben s-ar deplasa cu aceeași viteză (în aceeași direcție!), $K$ ar fi unu. Vom vedea mai departe cum anume depinde $K$ de viteza relativă a lui Alf și Ben. $K$ se numește uneori factorul de deplasare Doppler, iar efectul este similar cu cel al undelor sonore – trebuie să cunoașteți cu toții schimbarea sunetului produs de sirena unei ambulanțe sau a unei mașini de poliție pe măsură ce se apropie și apoi se îndepărtează.
Cum putem măsura $K$? Modalitatea evidentă este ca observatorii să țină evidența momentului în care semnalele luminoase sunt trimise și primite, astfel încât să poată calcula $T$ și $T^{\prime}$ și, prin urmare, $K$, atunci când se vor întâlni mai târziu. O altă posibilitate ar fi ca unul dintre ei să aibă un telescop foarte puternic cu care să urmărească ceasul celuilalt (aceasta este de fapt trenul care trece din nou pe lângă Big Ben!).
Trebuie să facem câteva presupuneri cu privire la acest număr $K$ pentru ca el să ne fie util. Presupunem mai întâi că atunci când Alf și Ben se deplasează cu viteze constante, atunci $K$ nu depinde de momentul în care se măsoară $T$ și $T^{\prime}$ și nici nu depinde de cât de mare este $T$. Astfel, de exemplu, dacă Alf așteaptă de două ori mai mult timp între trimiterea semnalelor luminoase, $K$ va fi același. Vedeți dacă puteți completa numerele $T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ în acest caz.
?

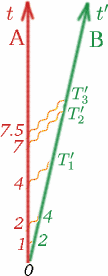
(Observați că este în regulă să începeți să măsurați timpul atunci când cei doi observatori sunt împreună, și amândoi își pot seta cronometrele la zero în acel moment). Deci, în general, avem
?

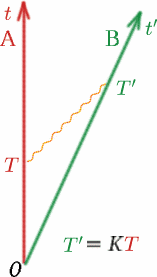
Al doilea lucru pe care îl presupunem, care este la fel de important, este că $K$ măsurat de Ben pentru semnalele luminoase de la Alf este același cu cel măsurat de Alf pentru semnalele luminoase de la Ben. De ce presupunem acest lucru? Imaginați-vă două mașini identice spate în spate pe un drum. Mașina $A$ stă pe loc, iar mașina $B$ se îndepărtează cu 50 km/oră$ de $A$. Pasagerii care privesc prin geamul din spate al lui $A$ vor vedea cum $B$dispare cu viteza corespunzătoare. Pasagerii din $B$ vor vedea o imagine foarte asemănătoare dacă se uită prin fereastra din spate – mașina $A$ va părea că se îndepărtează cu aceeași viteză! Ați avut vreodată experiența stranie de a sta într-un tren și de a crede că acesta tocmai s-a îndepărtat, când se dovedește că este vorba de trenul vecin care se deplasează în direcția opusă, iar trenul dumneavoastră este încă staționar?
Această ipoteză face posibil ca un observator să măsoare $K$ cu ajutorul radarului fără nicio cooperare din partea celuilalt. Poate cineva să ghicească cum? Să vă dau un indiciu.
Să presupunem, ca de obicei, că Alf și Ben se deplasează unul față de celălalt cu viteză constantă. Alf trimite două semnale la un interval de $T$, Ben le reflectă la intervalul $T^{\prime}$ și Alf le recepționează din nou la intervalul $T^{\prime\prime}$. Cum poate Alf să calculeze $K$??

Răspuns

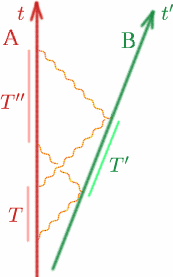
început{echipă} {T^{\prime}} = {K T} \quadru (9), \end{equation} \begin{equation} {T^{\prime\prime}} = {K T^{\prime}}\quad (10) \end{equation} Prin urmare, \begin{equation} {T^{\prime\prime}} = {K(K T)} = {K^2 T}\quad (11) \end{equation} deci avem \begin{equation} {K} = {\sqrt{T^{\prime\prime\prime}/T}}. \quad (12) \end{equation} Problemă Pentru a efectua o manevră complicată de andocare, este esențial ca două nave spațiale să fie ținute în repaus una față de cealaltă. Concepeți un experiment simplu pentru a verifica dacă acest lucru este așa.

Relația dintre K și viteză

Știm deja că dacă viteza relativă a lui Alf și Ben este zero, atunci $K$ = $1$. Care este valoarea sa pentru viteze generale? Există o modalitate inteligentă de a rezolva acest lucru, care folosește ideea despre care tocmai am vorbit, plus ideea de simultaneitate. Ce înseamnă aceasta? Voi explica într-un minut.
În primul rând, să ne imaginăm doi observatori obișnuiți care se îndepărtează unul de celălalt cu viteza constantă $v$. Să presupunem că, atunci când sunt împreună, amândoi își setează ceasurile la $t = 0$. La timpul $T$ al ceasului său, Alf emite un semnal radio; Ben îl reflectă înapoi la timpul $T’$ al ceasului său, iar Alf îl primește din nou la timpul $T^{\prime\prime}$ al ceasului său. Să facem un desen ca de obicei.
?

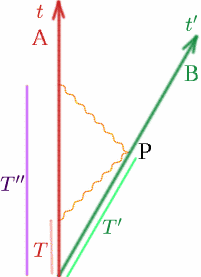
Acum știm că \begin{equation} {T^{\prime}} = {K T}\quadru (13) \end{equation} \begin{equation} {T^{\prime\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{equation} Deci Alf crede că timpul de deplasare al impulsului radio este \begin{equation} {T^{{\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{equation} și Alf calculează că distanța, $D$, dintre el și Ben, este jumătate din distanța parcursă de semnalul radio, ceea ce reprezintă jumătate din viteză înmulțită cu timpul: \begin{equation} {D} = {\frac {1} {2} c(K^2-1)T}. \quad (16) \end{equation} Acum știm că distanța dintre Alf și Ben se schimbă în mod constant, așa că trebuie să ne întrebăm când (adică la ce moment) aceasta este distanța dintre Alf și Ben. Aici avem nevoie de ideea de simultaneitate. Distanța este măsurată în mod clar atunci când Ben se află în punctul $P$, dar la ce moment corespunde acest lucru pentru Alf? Ei bine, Alf știe că impulsul radio parcurge aceeași distanță la dus și la întors, astfel încât evenimentul $Q$, pe care Alf îl consideră a fi în același timp cu $P$, va fi la jumătatea distanței dintre $T$ și $T^{\prime\prime}$. (Spunem că $Q$ este simultan cu $P$ pentru Alf – înseamnă doar că este în același timp). Așadar, timpul la $Q$ este \begin{equation} {T_Q} = {\frac {1} {2}(T+T”)} = {\frac {1}(T+T”)} = {\frac {1}(T+T”) {2} (K^2+1)T}. \quad (17) \end{equation} Astfel, Alf concluzionează că Ben a parcurs o distanță $D$ în timpul $T_Q$, deci viteza sa $v$ este dată de \begin{equation} {v} = {\frac {D} {T_Q}} = {\frac {\frac {\frac {1} {2} c(K^2-1)T} {\frac {1}{2}{2} (K^2+1)T}}. \quad (18) \end{equation} Prin urmare, avem \begin{equation} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \quad (19) \end{equation} Acum putem calcula $K$ în termeni de $\frac {v} {c}$: \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c} + \frac{v}{c}} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Prin urmare, \begin{equation} {K^2} = {\frac {1+ \frac{v}{c}} {K^2} = {\frac {1+ \frac{v}{c}}. {1- \frac{v}{c}}}\quad (23) \end{equation} și deci \begin{equation} {K} = \sqrt{{\left({\frac{1+\frac{v}{c}}{1-\frac{v}{c}}\drept)}}. \quad (24) \end{equation} Încercați să calculați câteva valori ale lui K:
de exemplu $v = c/4$ – care dă $K = \sqrt{5/3} = 1,291$.
Încercați acum $v = c/2, 9c/10, 99c/100$.
Acum nu mai contează dacă Alf este nemișcat și Ben se mișcă sau invers – $K$ este tot același. Ceea ce este diferit este dacă Alf și Ben se apropie unul de celălalt în loc să se îndepărteze – în acest caz, luăm valoarea lui $v$ ca fiind negativă, dar putem folosi aceeași formulă.
de exemplu, dacă Alf și Ben se apropie unul de celălalt cu viteza relativă $c/2$, \begin{equation} K = \sqrt{{\left({\frac{1+(-1/2)}{1-(-1/2)}}}\dreapta)}} = \sqrt{{\left({\frac{1/2}{3/2}}\dreapta)}} = \sqrt{1/3}. \quad (25) \end{equation}. Să calculăm $K$ pentru câteva viteze tipice:
1) avioane de linie care se apropie unul de altul cu viteza de 1000 km/oră$;
2) galaxiile din clusterul nostru care se îndepărtează cu viteze relative de 500 km/s$;
3) o mașină care se apropie de un polițist cu 100 km/oră$;
4) tu mergând spre prietenul tău cu 5 km/oră$ Credeți că vreunul din aceste efecte ar fi observabil? Paradoxul gemenilor – în sfârșit!
Ce se întâmplă? De ce este un paradox? (Ce înseamnă totuși cuvântul paradox?)
Să luăm în considerare gemenele identice, Albertina și Brigitta! Albertina stă acasă, la Londra, în timp ce Brigitta, cea aventuroasă, pleacă într-o călătorie în spațiu. Ea călătorește departe de Pământ timp de 6 ani, măsurați de ceasul ei, într-o navă spațială foarte rapidă care se deplasează cu $v = 4c/5$. Apoi se întoarce cu aceeași viteză timp de 6 ani. Astfel, Brigitta măsoară un timp de 12 ani pentru călătoria ei – este cu 12 ani mai în vârstă când se întoarce acasă la Albertina din Londra. Dar cât de bătrână este Albertina? Să vedem dacă presupunerea ta a fost corectă sau poate doar pe aproape!
Să desenăm o diagramă spațiu-timp: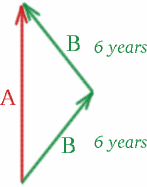
În călătoria de ieșire a Brigittei, gemenele se depărtează cu viteza relativă $v = 4c/5$, deci \begin{equation} {K^2} = {\frac{1+\frac{4}{5}}{1-\frac{4}{5}}} = {9}, \quad (26) \end{equation} și avem $K=3$. Pe drumul de întoarcere al Brigittei, ele se apropie una de cealaltă cu aceeași viteză, deci \begin{equation} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}}\quad (27) \end{equation} și $K=1/3$. Tot ce trebuie să facem pentru a calcula timpul pe care Albertina îl măsoară este să punem un semnal luminos! Aveți vreo sugestie unde?
Să presupunem că Albertina trimite un semnal în punctul $S$, ales astfel încât să ajungă la Brigitta la $U$, chiar în momentul în care aceasta este pe cale să se întoarcă.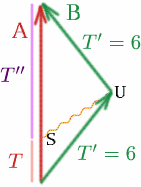
Atunci care este $T$ dacă $T^{\prime}=6$ și $K=3$? Avem \begin{equation} {T^{{\prime}} = {K T} \quad (28) \end{equation}
deci $6=3T$ și $T=2$.
Acum priviți ce se întâmplă pe drumul de întoarcere al Brigittei. Ce valoare are $T^{\prime\prime}$? Avem $T^{\prime}=6$, $K=1/3$ și \begin{equation} {T^{\prime}} = {K T^{\prime\prime\prime}}, \quad (29) \end{equation} deci $6=T^{\prime\prime\prime}/3$ și $T^{\prime\prime\prime}=18$. Prin urmare, timpul total măsurat de Albertina este de $T+T^{\prime\prime}=20$ ani, deci ea este cu 20 de ani mai în vârstă când se întâlnesc, în timp ce Brigitta este cu doar 12 ani mai în vârstă! Așadar, Albertina a îmbătrânit cu 8 ani mai mult decât Brigitta!
Ai ghicit corect????
Ce poți încerca să faci pe cont propriu sunt câteva experimente cu numere. De exemplu, vă puteți imagina că Brigitta face o călătorie de 10+10=20$ ani, să zicem, și puteți calcula cât de repede trebuie să călătorească pentru ca Albertina să fi îmbătrânit cu doar un an mai mult decât ea (adică au trecut 21$ ani pe ceasul Albertinei) când Brigitta se întoarce. Poate că vă puteți da seama dacă ar fi posibil să existe o călătorie spațială realistă (adică realizabilă) în care gemenii să îmbătrânească diferit cu o diferență notabilă!
Acum, de ce se numește toate acestea un paradox ? Vă amintiți ce înseamnă paradox ? Am spus mai devreme că, dacă două persoane se deplasează cu viteze constante (și, prin urmare, cu viteze constante una față de cealaltă), o mare parte din ceea ce se întâmplă este la fel indiferent dacă îl considerăm pe primul staționar și pe al doilea în mișcare, sau invers. Aplicând acest argument la Albertina și Brigitta,de ce nu am putea să o considerăm pe Brigitta în nava ei spațială ca fiind persoana care stă nemișcată, iar pe Albertina pe Pământ plecând și apoi revenind. Spus așa, sună destul de prostesc, dar sper că ați prins ideea. Atunci ne-am aștepta ca Brigitta să fie mai în vârstă decât Albertina atunci când se întâlnesc în cele din urmă. Dar am spus deja că Albertina este mai în vârstă atunci. Cum ar putea fi ambele afirmații adevărate? Acesta este paradoxul!
Vezi ce este greșit??
Ideea este că Brigitta nu se deplasează cu viteză constantă în raport cu Albertina pe toată durata călătoriei; ea are două secțiuni lungi de călătorie în care face acest lucru, dar între ele există o secțiune posibil scurtă, dar foarte importantă, în care deccelerează, se oprește și apoi accelerează în direcția opusă. Asta este ceea ce face diferența!Accelerația este un fenomen real, așa cum probabil știți de la atracțiile care vă fac să vă simțiți rău la un târg! Știți cum ar putea fi detectat cu un echipament simplu?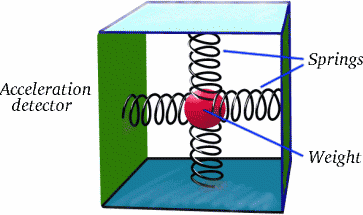
Și ce părere aveți despre toate acestea? Mi se pare un pic nedrept ca Brigitta să călătorească și să vadă mai mult din Univers, dar să sfârșească mai tânără decât sora ei geamănă care stă acasă – viața nu pare întotdeauna corectă! Dar asta ar trebui să vă încurajeze să călătoriți – nu neapărat în spațiu! – și să fiți aventuroși! Referință Pentru mai multe discuții despre paradoxul gemenilor și despre tehnicile descrise aici, puteți încerca să consultați cartea Flat and Curved Space-Times , de G. F. R. Ellis și de mine (publicată de Oxford University Press în 1988). Ați putea, de asemenea, să vă uitați la cărțile domnului Tompkins, care prezintă conceptele relativității speciale într-un mod amuzant și accesibil.

Puteți găsi recenzii ale cărților domnului Tompkins și le puteți comanda de pe site-ul Cambridge University Press, de exemplu, vedeți The New World of Mr Tompkins : The New World of Mr Tompkins : George Gamow’s Classic Mr. Tompkinsin Paperback

.