Introdução

Se você acompanhar este projeto, você será levado a uma conclusão surpreendente! Suponha que um de um par de gémeos idênticos vai numa viagem ao espaço e depois regressa para comparar a sua idade (digamos que ela) com a do outro gémeo que permaneceu no mesmo local na Terra. Acontece que depois da viagem, um dos gémeos será mais novo do que a sua irmã! Você deve estar perguntando como isso pode ser possível, e o objetivo deste projeto é mostrar a você como.
Deixe começar jogando um jogo de adivinhação – vamos descobrir se você está certo no final! Suponha que o gémeo viajante vai numa viagem de 12 anos – 6 anos fora e 6 anos atrás. Obviamente ela será 12 anos mais velha quando voltar. O que tens de fazer é adivinhar quanto mais velha será a gémea que não viaja….! Eu preciso te dizer o quão rápido o gêmeo em movimento viaja – digamos quatro quintos da velocidade da luz – embora eu ouse dizer que isso não vai te ajudar muito com seu palpite! Deixe-me sugerir-lhe que adivinhe um número inteiro entre 1 e 30!
Antes de considerarmos os gémeos, temos de criar certas ferramentas de que vamos precisar para compreender o que se está a passar. Vamos fazer muito uso de um certo tipo de gráfico chamado diagrama espaço-tempo. Não se preocupe se você nunca usou gráficos antes – vamos tentar começar pelo básico.
?

Gráficos

O mais simples tipo de gráfico é apenas uma imagem do que está acontecendo em uma superfície plana escolhida. Vamos assumir que você está sentado a uma mesa ou a uma mesa, e que você tem duas réguas e um grande pedaço de papel. Começando no canto inferior esquerdo, coloque uma régua ao longo do fundo e outra no lado esquerdo, com o papel em posição entre elas. O que você tem deve ser assim:

Chamaremos o ponto onde as duas réguas se encontram (o zero em ambas as escalas) a origem, ou O para abreviar, e as réguas fornecem os dois eixos . Seguindo a convenção, chamaremos de eixo x o que se encontra na parte inferior e eixo y o que se encontra na parte superior. Podemos rotular qualquer ponto no papel pelos seus valores de $x$ e $y$.Por exemplo, a origem tem $x=0$, $y=0$. O ponto $1cm$ do eixo y e $2cm$ do eixo x tem $x=1$, $y=2$ (eu realmente tenho estes valores ao contrário!).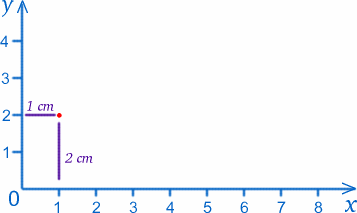

Exercise Draw your own graph and mark the following points:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Que forma formam?
Agora imagine algumas formigas com os pés muito sujos. Suponha que se caminha através do papel ficando sempre a uma distância de $1cm$ do eixo x. Seu caminho seria uma linha, descrita pela equação $y=1$ (uma maneira chique de dizer o que é dito em palavras na frase anterior). Outro poderia andar sempre a $3cm$ do eixo y; a equação do seu caminho seria $x=3$. Uma formiga um pouco mais original poderia caminhar de modo que a distância de ambos os eixos é sempre a mesma; ela passaria por $x=1$, $y=1$; $x=2$, $y=2$; etc. e seu caminho seria dado pela equação $x=y$.

Diagramas de tempo-espaço

Nesta seção, vamos desenhar alguns gráficos que parecem muito parecidos com os da seção anterior, mas seu significado será bastante diferente. Ainda temos dois eixos, e o etiquetado $x$ ainda representa a distância em uma determinada direção. No entanto o que foi rotulado $y$ está agora rotulado $t$, que representa o tempo, medido em segundos, digamos. Imagine por exemplo uma bola num ponto fixo $3cm$ de O; seu caminho no espaço-tempo será a linha reta $x=3$. Agora suponha que a bola rola ao longo de um caminho reto; então os pontos no gráfico corresponderiam às posições da bola em determinados momentos, por exemplo $x=5$, $t=4$ corresponderia ao fato da bola ser $5cm$ da origem $4$ segundos após o início da medição do tempo.
Exercise Plot points on the graph corresponding to the following events in the ball’s history: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. Como você interpretaria isto?
Tente agora $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. O que você observa sobre estes pontos?
Se o caminho da bola é uma linha reta no gráfico, significa que a bola está se movendo com velocidade constante (talvez velocidade zero). Nesse caso podemos calcular a velocidade vendo a distância que a bola percorre em um segundo – dividimos a variação do valor x pela variação correspondente do valor t. Assim, no nosso segundo exemplo, a velocidade da bola é de $2cm/sec$. Você concorda?
Exercise Draw um gráfico representando o movimento de uma bola que se move para trás e para frente entre dois pontos, com velocidade constante (mas periodicamente mudando de direção, é claro).
Agora vamos fazer algo bastante estranho ao nosso gráfico. Na teoria chamada relatividade especial , que é o que torna interessante pensar sobre gêmeos e viagens espaciais, muitas vezes precisamos plotar raios de luz em nossos gráficos. Agora os raios de luz viajam no espaço vazio com uma velocidade constante e muito grande (mas finita); um raio de luz que chegava até você a partir do sol deixou lá há cerca de $8$ minutos (as pessoas costumavam acreditar que a luz viajava infinitamente rápido para que você pudesse ver as estrelas no momento em que você as observava, mas agora se sabe que isso está errado). Para ser mais preciso, a velocidade da luz é de cerca de $30000000000cm/sec$! Isto pode levar a algumas escalas muito estranhas nos eixos de um gráfico espaço-tempo, por isso vamos escolher medir a distância de forma adiferente; as unidades no eixo x serão os segundos-luz, ou seja, a distância percorrida pela luz em um segundo. (Se a escala para $t$ for anos, a escala x correspondente será de anos-luz).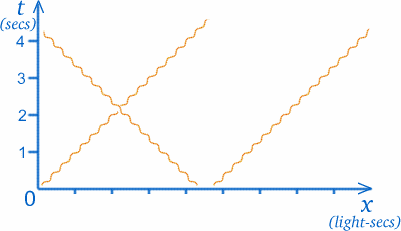
A grande vantagem disto é que o caminho de um raio de luz será sempre a $45$ graus para os eixos. Isto significa que um raio de luz através de O estará em ângulos iguais aos dois eixos, como você vê no diagrama. (Embora a luz viaje a uma velocidade constante, portanto seu caminho é uma linha reta, nós a representamos através de uma linha periclitante, como mostrado, para distinguir os raios de luz dos caminhos de outros objetos com massa.)
?

tempo de medição

Tendemos a assumir que quando as pessoas discordam sobre que horas são, o relógio de alguém está errado, ou talvez as pessoas estejam em fusos horários diferentes! Mas é ainda mais complicado do que isso! De acordo com a relatividade especial, duas pessoas podem estar no mesmo lugar e correlacionar seus relógios, mas se uma estiver se movendo em relação à outra, elas irão posteriormente discordar sobre que horas são. Infelizmente se você se juntar a um amigo e tentar testar esta teoria, você ficará desapontado, não porque a teoria está errada, mas porque na velocidade que você provavelmente será capaz de correr, mesmo que você seja um super-atleta, o efeito será muito pequeno para observar. É apenas quando as velocidades se tornam muito grandes (frações consideráveis da velocidade da luz) que este estranho fenômeno pode ser observado e, mesmo assim, apenas usando relógios extremamente precisos.
Para ver como isto poderia funcionar, vamos considerar uma “experiência de pensamento” semelhante a uma que Einstein sugeriu. (É uma experiência de “pensamento” em vez de uma experiência real, porque não pode ser realmente feita, como você vai perceber). Suponha que você observa o relógio no Big Ben através de um telescópio muito poderoso, enquanto você se afasta dele em um trem muito rápido que passou o relógio exatamente ao meio-dia (eu sei que o trem não passa pelo Big Ben, mas vamos fingir!). Agora, se o trem pudesse se mover à velocidade da luz, o que você veria acontecendo com os ponteiros do relógio? Pareceriam estar parados, ambos apontando para $12$! Porquê? Isto porque a luz emitida pelos (ou refletida pelos) ponteiros ao meio-dia estaria viajando longe do relógio exatamente na mesma velocidade que você no trem, e a luz emitida em horários posteriores não poderia alcançar o trem! Estranho!
Pode ver porque é que isto é uma “experiência de pensamento” (para além do facto de os comboios não passarem pelo Big Ben)? É porque um trem não poderia realmente se mover com a velocidade da luz (que é algo mais que a relatividade especial nos diz – qualquer objeto que pesa qualquer coisa nunca pode se mover tão rápido quanto a luz). Mas suponha que o trem se movia a metade da velocidade da luz (ainda muito rápido) – você veria os ponteiros do relógio se moverem, mas mais lentamente do que os do seu relógio! A medição do tempo depende de como você está se movendo!
Como isso pode ser? Para entender isso, vamos considerar um tipo especial de relógio, um relógio leve . Não é provável que você encontre um destes ao lado da sua cama, acordando-o pela manhã. Ele consiste em uma fonte de luz que emite sinais que percorrem uma distância D e são depois refletidos de volta à fonte. O intervalo de tempo ou intervalo entre cada vez que um sinal é enviado e quando ele é recebido de volta, define os ticks do relógio; eles ocorrem na hora $2T$ separados, onde \begin{equação} {T} = {D/c} \com $c$ representando a velocidade da luz. (Lembre-se que velocidade = distância/tempo, então tempo = distância/velocidade.)

Agora vamos supor que um foguete em movimento carrega tal relógio – a experiência da tripulação será que os ticks ocorrem em intervalos de $2T$. Agora suponhamos que a tripulação de um foguete parado observe o relógio do foguete em movimento, e compare-o com o seu próprio, também fazendo tic-tac em intervalos de $2T$. O que é que eles vão ver? Os diagramas abaixo devem sugerir a resposta. (Lamento que os meus foguetes pareçam mais peixes!)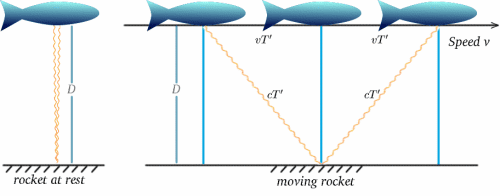
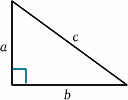
Para o foguetão em movimento, a luz é reflectida do espelho a meio tempo entre quando o sinal é enviado e quando é reflectido de volta. Do foguete estacionário, o tempo de viagem parece ser $2T^{ \prime}$, digamos. Podemos resolver isto usando um teorema muito importante (um nome extravagante para algo que provou ser verdade em matemática!) – o de Pitágoras.

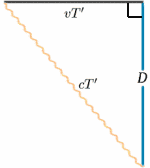\begin{equação} {a^2 + b^2} = {c^2} \(1) fim (equação) No diagrama do foguete, temos um triângulo em ângulo recto, por isso… D^2 + v^2 T^{‘2} = {c^2 T ^2 T ^{\prime 2}}}}quad (2) ^end{equação} Agora resolvemos isto por $T^{\prime}$: \Inicio (c^2 – v^2) = = D^2, qad (3) fim (equação) \c^2 (1 – v^2/{c^2})} = {D^2} (4),end{\i1}end{\i1}dando {\i}begin{\i}{T^{\i}prime} = {\i1}frac {\i} (1 – v^2/{c^2})|quad (5) ^end{equação (5) ^end{equação (6) ^end{equação (6) ^end{equação (6) ^sqrt{(1 – v^2/{c^2})}, ^quad (6) ^end{equação (6) ^end{equação (6) e as taxas do relógio serão diferentes (a menos que, claro, $v=0$). De facto $T^{\prime}$ é maior que $T$, por isso parece à tripulação estacionária como se o relógio em movimento tivesse intervalos mais longos entre os ticks e por isso está a ir devagar.
A partir do momento que aceitamos que não existe uma definição universal de tempo que se aplique a todos, temos de pensar no que realmente queremos dizer ao medir o tempo. Em certo sentido, estamos a medir distâncias ao longo dos nossos caminhos no espaço-tempo (pense no diagrama espaço-tempo). Os gêmeos seguem caminhos diferentes no espaço-tempo, por isso não é tão surpreendente que eles tenham experimentado quantidades diferentes de tempo.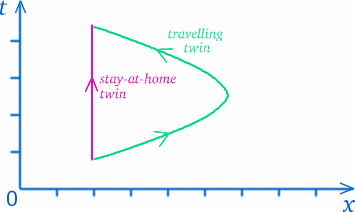
Mas não tire conclusões precipitadas – as coisas nem sempre são o que parecem…! O caminho do gémeo viajante parece mais longo, mas será que isso significa que ela já experimentou mais tempo? Para ver como este tipo de pergunta é complicada, pense numa situação que pode ser bastante semelhante. Suponha que você mora em Trumpington, no lado sul de Cambridge, e quer ir às compras no Tesco’s, no extremo norte do centro da cidade (o mais próximo possível, evitando zonas pedonais), na estrada circular ou no by-pass – veja o diagrama abaixo.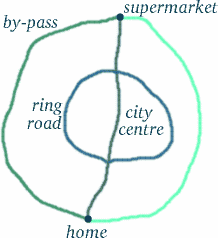
Na maioria das vezes do dia, você descobriria que o percurso mais longo – o by-pass – levava menos tempo, seguido pela estrada circular. Está agora convencido de que a resposta óbvia nem sempre é a correcta??
Vimos como o tempo é medido utilizando sinais luminosos. Uma vez que temos um relógio preciso, podemos então medir a distância usando sinais de luz ou radar refletidos do objeto distante; a distância será metade do tempo de viagem da luz, multiplicada pela velocidade da luz.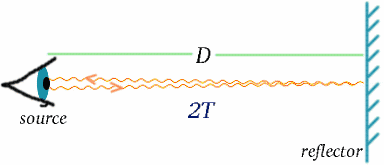

\begin{equation} {D} = {cT}\quad (7) {cT}}end{equation Como o tempo, a distância é uma quantidade em que o resultado da medição depende da forma como o observador está se movendo.

Factores K

Descrevo agora uma ideia que nos deve ajudar a fazer cálculos do tipo de efeito de que vos tenho falado.
Se um astronauta B (para Ben) estiver num foguete movendo-se à velocidade $c/5$ de outro astronauta A (para Alf) numa estação espacial. Uma vez por ano, no dia 13 de março, Alf envia saudações de aniversário ao Ben. Suponha que a mensagem de rádio com esta saudação no ano de 2010 seja medida pela estação espacial para percorrer uma distância de meio ano-luz para chegar ao foguete, demorando meio ano para chegar ao foguete. A mensagem seguinte é enviada exatamente um ano depois. Quando este sinal de rádio tiver viajado por meio ano até onde Ben, o astronauta, recebeu o sinal anterior, o foguete se moveu um quinto de um ano-luz mais adiante, então este sinal tem que viajar por mais tempo para alcançar o foguete; na verdade, o tempo medido por Alf quando o sinal chega ao foguete é de três quartos de um ano depois de ter sido enviado – veja o diagrama abaixo. O pobre Alf conclui que as saudações de aniversário enviadas anualmente serão recebidas por Ben em intervalos de um ano e um quarto de ano, de acordo com o relógio de Alf.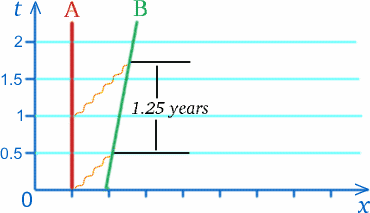
Isso não nos diz o que Ben vai medir para esses intervalos, mas sugere que pode muito bem não ser um ano! Um efeito semelhante acontecerá para os sinais enviados pelo Ben ao Alf.
Agora vamos olhar para o caso geral e tornar isto mais preciso. Considere dois observadores, Alf e Ben, afastando-se um do outro a velocidades constantes.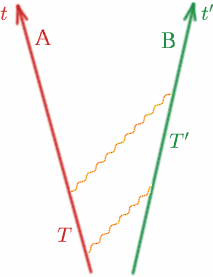
Alf envia um sinal de luz e depois outro no momento $T$ mais tarde. Ben recebe os dois sinais às vezes $T^{\prime}$ separados, de acordo com o seu relógio. Depois definimos uma quantidade $K$ por {equação} {K} = {T^{\prime}/T}. \(8) final (equação) Note que se Alf e Ben estivessem se movendo com a mesma velocidade (na mesma direção!), $K$ seria um. Vamos ver precisamente como $K$ depende da velocidade relativa do Alf e do Ben. $K$ é por vezes chamado factor de desvio Doppler e o efeito é semelhante ao das ondas sonoras – todos devem conhecer a mudança de som da sirene de uma ambulância ou de um carro da polícia à medida que se aproxima e depois retrocede.
Como podemos medir $K$? A forma óbvia é os observadores manterem registos de quando os sinais luminosos são enviados e recebidos para que possam calcular $T$ e $T^{\prime}$, e portanto $K$, quando se encontrarem mais tarde. Outra possibilidade seria um ter um telescópio muito poderoso com o qual observar o relógio do outro (este é realmente o comboio a passar pelo Big Ben tudo de novo!).
Temos de fazer algumas suposições sobre este número $K$ para que ele nos seja útil. Nós assumimos primeiro que quando Alf e Ben estão se movendo com velocidades constantes, então $K$ não depende de quando $T$ e $T^{\prime}$ são medidos, nem depende de quão grande é $T$. Assim, por exemplo, se Alf esperar o dobro do tempo entre o envio de sinais de luz, $K$ será o mesmo. Veja se pode preencher os números$T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ neste caso.
?

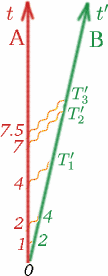
(Repare que não há problema em começar a medir o tempo quando os dois observadores estão juntos, e ambos podem ajustar os seus cronómetros para zero nesse momento). Assim, em geral temos
?

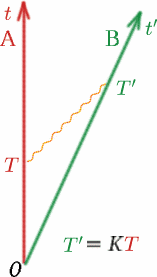
A segunda coisa que assumimos, que é igualmente importante, é que os $K$ medidos por Ben para sinais de luz de Alf é o mesmo que medido por Alf para sinais de luz de Ben. Por que assumimos isto? Imagine dois carros idênticos de volta para trás em uma estrada. O carro $A$ fica parado e o carro $B$ sai a $50km/hr$ longe de $A$. Os passageiros que olharem pela janela traseira do $A$ verão o $B$ a desaparecer à taxa apropriada. Passageiros em $B$ verão uma imagem muito semelhante se olharem pela janela de trás – o carro $A$ parecerá estar a afastar-se à mesma velocidade! Alguma vez você já teve aquela experiência incrível de sentar em um trem e pensar que ele acabou de se mover, quando se descobre que era o trem vizinho se movendo na direção oposta e seu trem ainda está estacionário?
Esta suposição torna possível para um observador medir $K$ pelo radar sem qualquer cooperação do outro. Alguém pode adivinhar como? Deixe-me dar-lhe uma dica.
Conteonte como sempre que o Alf e o Ben se estão a afastar com velocidade constante. Alf envia dois sinais a um intervalo de $T$, Ben os reflete no intervalo $T^{\prime}$ e Alf os recebe de volta no intervalo $T^{\prime}$. Como pode Alf trabalhar $K$?
?

Resposta

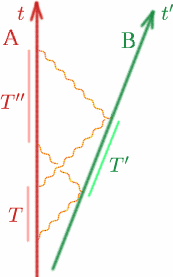
\begin{equação} {T^{\prime}} = {K T} \(9), end (equação) \begin (equação) = K T^ T^ T^ Preme (10) final (equação) Por isso, temos a equação de início = K(K T){K(K T)} = K(K^2 T^2 T}quad (11) end{equation} so we have {begin{equation} {K} = {sqrt{T^{prime=prime/T}}. \Quadrado (12) final (equação) Problema Para realizar uma manobra de acoplagem complicada, é essencial que duas naves espaciais sejam mantidas em repouso uma em relação à outra. Faça uma experiência simples para verificar se é assim.

A relação entre K e velocidade

Já sabemos que se a velocidade relativa de Alf e Ben é zero, então $K$ = $1$. Qual é o seu valor para as velocidades gerais? Há uma forma inteligente de resolver isto, que usa a ideia que acabamos de falar, mais a ideia de simultaneidade. O que é que isso significa? Explicarei sobre isso em um minuto.
Primeiro vamos imaginar nossos dois observadores habituais viajando longe um do outro com velocidade constante $v$. Suponhamos que quando estão juntos, ambos fixam os relógios em $t = 0$. Na hora $T$ pelo seu relógio, Alf emite um sinal de rádio; Ben reflete de volta na hora $T’$ pelo seu relógio e Alf o recebe de volta na hora $T^{\prime}$ pelo seu relógio. Vamos fazer um desenho como de costume.
?

Agora sabemos que \begin{equação} {T^{\prime}} = {K T}{K T}{quad (13) ^end{equação} \Begin (equação) {T^{\prime}} = {K T^{\prime}} = {K^2 T}. \(14) final (equação) Então Alf acha que o tempo de viagem para o pulso de rádio é de início. T^^2 T-T = {K^2-1 T-T} = {(K^2-1)T}, ^quad (15) end{equation} e Alf trabalha que a distância, $D$, entre ele e Ben, é metade da distância percorrida pelo sinal de rádio , que é metade da velocidade vezes o tempo: \begin (equação) =frac (1) c(K^2-1)T}. (16) end{\i1}end{\i1} Agora sabemos que a distância entre Alf e Ben está em constante mudança, por isso temos de perguntar quando (ou seja, a que horas) esta é a distância entre Alf e Ben. É aqui que precisamos da ideia de simultaneidade. A distância é claramente medida quando o Ben está no ponto $P$, mas a que horas é que isto corresponde para o Alf? Bem, o Alf sabe que o pulso do rádio percorre a mesma distância para fora e para trás, por isso o evento $Q$, que o Alf julga estar ao mesmo tempo que $P$, estará a meio caminho entre $T$ e $T^{\prime}$. (Dizemos que $Q$ é simultâneo com $P$ para o Alf – apenas significa ao mesmo tempo). Portanto, o tempo em $Q$ é $T_Q} = $Frac 1. {2}(T+T”)} = {1}frac {1} {2} (K^2+1)T}. \(17) end (equação) Assim Alf conclui que Ben viajou uma distância de $D$ no tempo $T_Q$, então sua velocidade $v$ é dada por {v} {v} = {\i}frac {D} = {T_Q} = {\i1}frac {\i} c(K^2-1)T} c(K^2-1)T} {\i1}{\i}{\i1} (K^2+1)T}}}. \(18) end (equação) Por isso, temos a “equação de início” = = = =frac = =K^2-1} =K^2+1}}. \”Quad” (19) “End” (equação) Agora podemos trabalhar com $K$ em termos de $Frac {v} {c}$: \begin (equação) {(K^2+1)|frac {v} = {K^2-1}, qad (20) end (equação) \begin (equação) {K^2frac{v}{c} +frac{v}{c} = {K^2-1}, {K^2-1}, {quad (21) end{equation} \begin (equação) {1+frac (v}{c}} ={K^2(1-frac{v}{c}), {quad (22) {final (equação) Por isso, begin{equação} {K^2} = {1+frac {v}{c}} 1-frac (vc) (23) final (e por isso, primeira (equação) (k) =qrt (esquerda) (frac (1+frac) (vc)) (1-frac (vc) (direita) \(24) final (equação) Tente trabalhar alguns valores de K:
e.g. $v = c/4$ – isso dá $K = \sqrt{5/3} = 1.291$.
Tente agora $v = c/2, 9c/10, 99c/100$.
Agora não importa se Alf está parado e Ben está se movendo ou o contrário – $K$ ainda é o mesmo. O que é diferente é se Alf e Ben estão se aproximando um do outro ao invés de se moverem separados – nesse caso, tomamos o valor de $v$ como negativo, mas podemos usar a mesma fórmula.
e.g. se Alf e Ben se aproximam com relativa velocidade $c/2$, \begin{equação} K = {\i1+(-1/2)}{1-(-1/2)}{1-(-1/2)}{1-direita)} = {1-esquerda(1/2)} = {1/2){3/2}{1/2}direita)} = {11/3}. \Esquadra (25) final (equação). Vamos trabalhar $K$ para algumas velocidades típicas:
1) aviões a aproximarem-se uns dos outros com velocidade $1000km/hr$;
2) galáxias no nosso aglomerado a afastarem-se com velocidades relativas de $500km/s$;
3) um carro a aproximar-se de um polícia a $100km/hr$;
4) você a caminhar em direcção ao seu amigo a $5km/hr$ Acha que algum destes efeitos seria observável? O paradoxo dos gêmeos – finalmente!
O que acontece? Porque é que é um paradoxo? (O que a palavra paradoxo significa afinal?)
Vamos considerar gêmeos idênticos, Albertina e Brigitta! A Albertina fica em casa em Londres, enquanto a Brigitta, a aventureira, vai numa viagem espacial. Ela viaja para longe da Terra por 6 anos, como medido pelo seu relógio, em uma nave espacial muito rápida que viaja a $v = 4c/5$. Ela então retorna na mesma velocidade por 6 anos. Então Brigitta mede um tempo de 12 anos para sua viagem – ela é 12 anos mais velha quando ela volta para casa, em Albertina, Londres. Mas quanto tempo mais velha é a Albertina? Vamos ver se o seu palpite estava certo ou talvez apenas perto!
Deixe desenhar um diagrama espaço-tempo: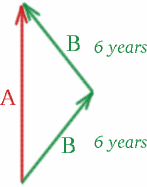
Na viagem de Brigitta, os gêmeos se afastam com velocidade relativa $v = 4c/5$, então, {K^2} = {\an8} = {\an8}frac{1+frac{4}{5}}}{1-frac{4}{5}} = {9}, {\an8}final{\an8} e nós temos $K=3$. Na viagem de regresso da Brigitta, eles aproximam-se com a mesma velocidade, por isso, primeiro (K^2) = 1-Frac (1-Frac) (4) (5) (1++Frac) (4) (5) (27) (27) (Fim (27) (Fim (equação)) e $K=1/3$. Tudo o que precisamos de fazer para calcular o tempo que o Albertina mede é colocar um sinal luminoso! Alguma sugestão onde?
Ponha Albertina envia um sinal no ponto $S$, escolhido para que ele chegue a Brigitta a $U$, no momento em que ela está prestes a dar a volta.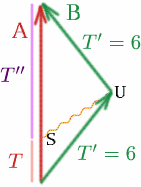
Então o que é $T$ se $T^{\prime}=6$ e $K=3$? Temos {\a10}{T^{\a10} = {K T} \(28) {\an8}
so $6=3T$ e $T=2$.
Agora olha o que acontece na viagem de regresso da Brigitta. O que é $T^{\prime=prime=$? Nós temos $T^{\prime}=6$, $K=1/3$ e $T^{\prime}=K T^{\prime}=, QAD (29) end{\i} so $6=T^{\prime=/3$ e $T^{\prime=18$. Portanto, o tempo total medido por Albertina é $T+T^{\prime\prime}=20$ anos, então ela é 20 anos mais velha quando eles se encontram, enquanto Brigitta é apenas 12 anos mais velha! Então a Albertina tem mais 8 anos do que a Brigitta!
Então você adivinhou corretamente????
O que você pode tentar fazer por conta própria são algumas experiências com números. Por exemplo, você pode imaginar que Brigitta faz uma viagem de $10+10=20$ anos digamos, e você pode descobrir quão rápido ela tem que viajar para Albertina ter envelhecido por apenas mais um ano do que ela envelheceu (ou seja, $21$ anos se passaram no relógio de Albertina) quando Brigitta voltar. Talvez você possa descobrir se seria possível uma viagem espacial realista (ou seja, realizável) na qual os gêmeos envelheceriam de forma diferente por uma quantia notável!
Agora por que tudo isso é chamado de paradoxo ? Lembra-se do que significa paradoxo? Dissemos anteriormente que se duas pessoas estão se movendo com velocidades constantes (e, portanto, constantes em relação uma à outra), muito do que acontece é o mesmo, quer consideremos a primeira estática e a segunda estática, quer o contrário. Aplicando esse argumento a Albertina e Brigitta, porque não podemos considerar a Brigitta na sua nave espacial como a pessoa que fica quieta, e a Albertina na Terra navegando para longe e depois voltando. Dito assim, parece um pouco idiota, mas espero que tenhas percebido a ideia. Então esperamos que a Brigitta seja mais velha que a Albertina quando finalmente se encontrarem. Mas nós já dissemos que a Albertina é mais velha nessa altura. Como é que estas duas declarações podem ser verdadeiras? Isso é oparadox!
Pode você ver o que está errado???
O ponto é que Brigitta não está se movendo com velocidade constante em relação à Albertina em toda a sua jornada; ela tem dois longos trechos de jornada nos quais ela faz isso, mas no meio há um trecho possivelmente curto mas muito importante onde ela desacelera, pára e depois acelera na direção oposta. Isto é o que faz toda a diferença! Aceleração é um fenômeno real, como você provavelmente sabe pelos passeios que fazem você se sentir doente em uma feira! Sabe como pode ser detectado com um simples equipamento?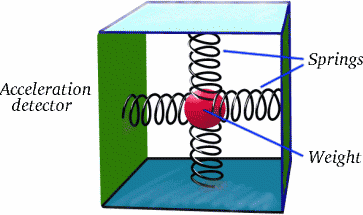
Então o que você acha de tudo isso? Parece um pouco injusto que Brigitta consiga viajar e ver mais do Universo, mas acabe mais nova do que a sua irmã gémea que fica em casa – a vida nem sempre parece justa! Mas deve encorajá-la a viajar – não necessariamente no espaço! – e a ser aventureira! Referência Para mais discussões sobre o paradoxo dos gêmeos e as técnicas aqui descritas, você pode tentar olhar o livro Flat and Curved Space-Times , de G. F. R. Ellis e eu (publicado pela Oxford University Press em 1988). Você também pode olhar os livros do Sr. Tompkins que introduzem os conceitos de relatividade especial de uma forma divertida e acessível.

Você pode encontrar resenhas dos livros do Sr. Tompkins e encomendá-las no site da Cambridge University Press, por exemplo, veja The New World of Mr Tompkins : George Gamow’s Classic Mr. Tompkinsin Paperback