Odkryj pochodzenie dzielenia i mnożenia
W dzisiejszym poście wyjaśnimy pochodzenie symboli matematycznych dzielenia i mnożenia.
Symbol podziału:
Było wiele sposobów oznaczania dzielenia, a my zamierzamy wyjaśnić pochodzenie niektórych symboli najczęściej używanych i najlepiej znanych przez wszystkich.
Poziomy pasek ułamków, wprowadzony przez Arabów, został po raz pierwszy użyty w Europie przez matematyka Fibonacciego w XIII wieku, choć jego zastosowanie rozpowszechniło się dopiero w XVI wieku.
Skośny pasek, wariant poziomego, został wprowadzony przez De Morgana w 1845 roku. Był to środek typograficzny w książkach drukowanych, aby można było zapisać ułamek w jednej linii. Symbol, który jest dziś powszechnie używany do wyrażania dzielenia:
Kolejnym ze znaków był nawias, choć obecnie nie jest on zbyt często używany. Aby wyrazić 21 podzielne przez 3, napisalibyśmy 21) 3, a wynik dzielenia umieścili po prawej stronie po kolejnym nawiasie: 21) 3 (7. 
Znak ten znajduje się w dziele Arithmetica integra (1544) niemieckiego matematyka Michaela Stiefela.
Ten sam matematyk używał również wielkich liter M i D do oznaczania mnożenia i dzielenia w swoim dziele Deutsche Arithmetica (1545). Inni autorzy również używali D, w tym jako odwróconego D, jak Francuz J. E. Gallimard (1685-1771), a inni jako opadającego d, jak Portugalczyk J. A. da Cuhna (1744-1787).
Jednym z nadal używanych symboli dzielenia jest słupek z punktem powyżej i poniżej. Został on wprowadzony przez szwajcarskiego matematyka, Johanna Heinricha Rahna, w jego dziele Teutsche Algebra (1659). Ten znak podziału jest bardzo graficzny, do tego stopnia, że pasek ułamka jest normą ogólną.
Symbol ten nie odniósł sukcesu w jego ojczyźnie, Szwajcarii, ani w Europie. Jednak był zarówno w Wielkiej Brytanii, jak i w Stanach Zjednoczonych. W szczególności, jest to nadal symbol używany na kalkulatorach do dzielenia.
Niemiecki matematyk, Gottfried W. Leibniz, wprowadził dwa punkty ( : ) i jest to obecnie najczęściej używany symbol. Według Leibniza, jedną z zalet stosowania tego symbolu jest to, że dzielenie może być utrzymywane wzdłuż tej samej linii i utrzymuje związek dzielenia z mnożeniem, do którego Leibniz używał punktu.
Jeśli chodzi o gnomon lub kąt, którego używamy do oddzielenia czynników dzielenia (dywidendy, dzielnika i ilorazu), nie ma zbyt wielu informacji.
Ale Boyer, w swojej Historii Matematyki, str. 282, mówi: „Arabowie, a przez nich później Europejczycy, przyjęli większość swoich arytmetycznych sztuczek od Hindusów, a więc jest bardzo prawdopodobne, że metoda „długiego podziału” znana jako „metoda galer” przez swoje podobieństwo do statku z rozwiniętymi żaglami, również pochodzi z Indii.” Najwyraźniej „metoda galer” wykorzystywała kąt podobny do obecnie stosowanego.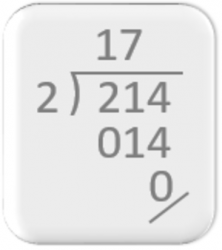
Symbol mnożenia:
W czasach Babilończyków używali oni ideogramu: „a-du”. W manuskrypcie Bakhshiili, najstarszym manuskrypcie indyjskiej matematyki, umieścili jeden czynnik obok siebie i nic więcej. Indyjski matematyk Bhaskara Acharia (1114-1185) użył słowa „bhavita” lub „bha” zaraz po czynnikach.
Inni matematycy używali litery M dla mnożenia i litery D dla dzielenia, jak powiedzieliśmy wcześniej.
W dawnych czasach arytmetyki wiele algorytmów wykorzystywało krzyż z San Andres do rozwiązywania iloczynów dzielenia i mnożenia oraz proporcji. Być może z tego powodu w 1631 roku Oughtred, wybrał ten krzyż jako symbol mnożenia.
Doświadczył on wielkiej akceptacji, z wyjątkiem matematyków Gottfrieda W. Leibniza i Isaaca Newtona, którzy nie czuli się w pełni komfortowo z tym symbolem. Leibniz, w 1698 roku, w jednym z listów do matematyka Johanna Bernoulliego, pisze: „Nie lubię symbolu × jako symbolu mnożenia, ponieważ można go pomylić z x; … Często po prostu odnoszę dwie wielkości za pomocą punktu i oznaczam mnożenie przez RS – PQ.”
Z tego powodu Leibniz wprowadził kropkę jako symbol mnożenia.
Były też inne symbole mnożenia. Na przykład szwajcarski matematyk Johann Rahn (1622-1676) w swoim dziele Teutsche Algebra (1659) użył gwiazdki *. Podobnie jak Leibniz, który wcześniej użył upadłego C, otwartą stroną w dół, w swoim Dissertatio of combinatorial art (1666).
Mam nadzieję, że ten post o dzieleniu i mnożeniu oraz symbolach, których używamy do ich wyrażania był interesujący.
Jeśli chcesz kontynuować naukę o dzieleniu i mnożeniu, zapisz się do Smartick i wypróbuj go za darmo.
Learn More:
- Symbole matematyczne: Greater Than, Less Than, i równe
- Symbole większe i mniejsze
- Symbole matematyczne do przedstawiania operacji i relacji
- Naucz się używać liczb rzymskich
- Jak rozwiązywać Operacje zespolone
- Autor
- Czasowe posty
Wielodyscyplinarny i wielokulturowy zespół składający się z matematyków, nauczycieli, profesorów i innych specjalistów w dziedzinie edukacji!
Dążą do stworzenia jak najlepszych treści matematycznych.
- Examples of 3rd Grade Math Word Problems with Solutions – 03/25/2021
- Consecutive Interior Angles: Czym są i jak je znaleźć z przykładami – 03/11/2021
- Przykłady zadań z matematyki dla drugiej klasy z rozwiązaniami – 02/04/2021
.