Introduction

Si vous suivez ce projet, vous serez amené à une conclusion étonnante ! Supposons que l’un des deux jumeaux identiques parte en voyage dans l’espace et revienne ensuite pour comparer son âge (disons le sien) avec celui de l’autre jumeau resté au même endroit sur Terre. Il s’avère qu’après le voyage, l’un des jumeaux sera plus jeune que sa sœur ! Vous devez vous demander comment cela est possible, et le but de ce projet est de vous montrer comment.
Commençons par jouer aux devinettes – nous saurons si vous avez raison à la fin ! Supposons que la jumelle voyageuse parte pour un voyage de 12 ans – 6 ans à l’aller et 6 ans au retour. Il est évident qu’elle aura 12 ans de plus à son retour. Ce que vous devez faire, c’est deviner quel sera l’âge du jumeau qui n’a pas voyagé…. ! Je dois vous dire à quelle vitesse voyage le jumeau en mouvement – disons quatre cinquièmes de la vitesse de la lumière – mais j’ose dire que cela ne vous aidera pas beaucoup à deviner ! Laissez-moi vous suggérer de deviner un nombre entier entre 1 et 30 !
Avant de considérer les jumeaux, nous devons mettre en place certains outils dont nous aurons besoin pour comprendre ce qui se passe. Nous utiliserons beaucoup un certain type de graphique appelé diagramme espace-temps. Ne vous inquiétez pas si vous n’avez jamais utilisé de graphiques auparavant – nous allons essayer de commencer par les bases.
?

Graphes

La sorte de graphique la plus simple est juste une image de ce qui se passe sur une surface plane choisie. Supposons que vous soyez assis à une table ou à un bureau, et que vous ayez deux règles et une grande feuille de papier. En commençant par le coin inférieur gauche, placez une règle le long du bas et une autre le long du côté gauche, avec le papier en position entre les deux. Ce que vous avez devrait ressembler à ceci:

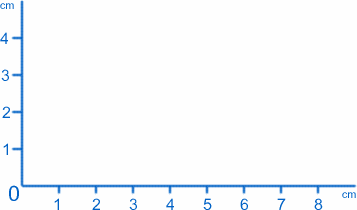
Nous appellerons le point où les deux règles se rencontrent (le zéro sur les deux échelles) l’origine, ou O pour faire court, et les règles fournissent les deux axes . Par convention, nous appellerons celui qui se trouve le long du bas l’axe x, et celui qui se trouve le long du côté l’axe y . Nous pouvons étiqueter n’importe quel point sur le papier par ses valeurs de $x$ et $y$. Par exemple, l’origine a $x=0$, $y=0$. Le point à 1cm$ de l’axe des y et à 2cm$ de l’axe des x a $x=1$, $y=2$ (je les ai vraiment dans le bon sens !).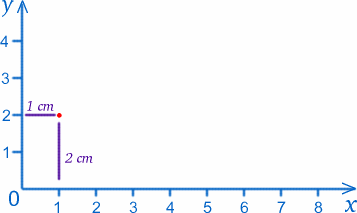

Exercice Dessinez votre propre graphique et marquez les points suivants:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
Quelle forme forment-ils ?
Imaginez maintenant des fourmis aux pieds très sales. Supposons qu’une d’entre elles marche sur le papier en restant toujours à une distance de 1cm$ de l’axe des x. Son chemin serait une ligne, décrite par l’équation $y=1$ (une façon fantaisiste de dire ce qui est dit en mots dans la phrase précédente). Une autre fourmi pourrait marcher toujours à 3 cm de l’axe des y ; l’équation de son chemin serait $x=3$. Une fourmi un peu plus originale pourrait marcher de façon à ce que sa distance par rapport aux deux axes soit toujours la même ; elle passerait par $x=1$, $y=1$ ; $x=2$, $y=2$ ; etc et son chemin serait donné par l’équation $x=y$.

Diagrammes espace-temps

Dans cette section, nous allons dessiner des graphiques qui ressemblent beaucoup à ceux de la section précédente, mais leur signification sera assez différente. Nous avons toujours deux axes, et celui étiqueté $x$ représente toujours la distance dans une certaine direction. Imaginez par exemple une balle en un point fixe situé à 3 cm de O ; sa trajectoire dans l’espace-temps sera la ligne droite $x=3$. Supposons maintenant que la balle roule le long d’une trajectoire rectiligne ; alors les points du graphique correspondraient aux positions de la balle à des instants particuliers par exemple $x=5$, $t=4$ correspondrait au fait que la balle se trouve à 5cm$ de l’origine 4$ secondes après le début de la mesure du temps.
Exercice Tracez sur le graphique les points correspondant aux événements suivants dans l’histoire de la balle : $x=4$, $t=1$ ; $x=4$, $t=2$ ; $x=4$, $t=3$. Comment interprétez-vous cela ?
Essayez maintenant $x=1$, $t=1$ ; $x=3$, $t=2$ ; $x=5$, $t=3$. Que remarquez-vous à propos de ces points ?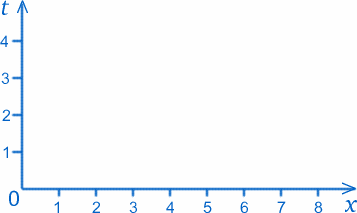
Si la trajectoire de la balle est une ligne droite sur le graphique, cela signifie que la balle se déplace à vitesse constante (peut-être à vitesse nulle). Dans ce cas, nous pouvons calculer la vitesse en voyant la distance parcourue par la balle en une seconde – nous divisons la variation de la valeur x par la variation correspondante de la valeur t. Ainsi, dans notre deuxième exemple, la vitesse de la balle est de $2cm/sec$. Êtes-vous d’accord ?
Exercice Dessinez un graphique représentant le mouvement d’une balle qui se déplace en avant et en arrière entre deux points, avec une vitesse constante (mais en changeant périodiquement de direction, bien sûr).
Nous allons maintenant faire quelque chose d’assez étrange à notre graphique. Dans la théorie appelée relativité restreinte , qui est ce qui rend intéressant de penser aux jumeaux et aux voyages dans l’espace, nous avons souvent besoin de tracer des rayons lumineux sur nos graphiques. Or, les rayons lumineux voyagent dans l’espace vide à une vitesse constante et très élevée (mais finie) ; un rayon de lumière qui vous parvient du soleil est parti de là il y a environ 8$ minutes (on croyait autrefois que la lumière voyageait infiniment vite, de sorte que l’on pouvait voir les étoiles au moment où on les observait, mais on sait maintenant que c’est faux). Pour être plus précis, la vitesse de la lumière est d’environ $30000000000cm/sec$ ! Cela pourrait conduire à des échelles très étranges sur les axes d’un graphique de l’espace-temps, nous choisirons donc de mesurer la distance d’une manière différente ; les unités sur l’axe des x seront les secondes-lumière, c’est-à-dire la distance parcourue par la lumière en une seconde. (Si l’échelle pour $t$ est les années, l’échelle x correspondante sera les années-lumière).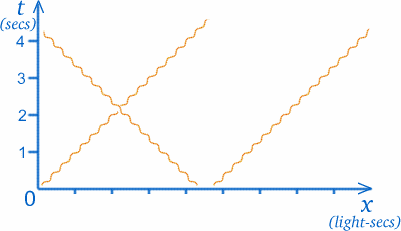
Le grand avantage de cette méthode est que le trajet d’un rayon lumineux sera toujours à $45$ degrés par rapport aux axes. Cela signifie qu’un rayon lumineux passant par O fera des angles égaux par rapport aux deux axes, comme vous le voyez sur le diagramme. (Bien que la lumière voyage à une vitesse constante, de sorte que sa trajectoire est une ligne droite, nous la représentons par une ligne ondulée, comme indiqué, pour distinguer les rayons lumineux des trajectoires d’autres objets ayant une masse.)
?

Mesurer le temps

Nous avons tendance à supposer que lorsque les gens ne sont pas d’accord sur l’heure qu’il est, la montre de quelqu’un est fausse, ou peut-être que les gens sont dans des fuseaux horaires différents ! Mais c’est encore plus compliqué que cela ! Malheureusement, si vous faites équipe avec un ami pour essayer de tester cette théorie, vous serez déçu, non pas parce que la théorie est fausse, mais parce qu’à la vitesse à laquelle vous êtes susceptible de courir, même si vous êtes un super-athlète, l’effet sera trop faible pour être observé. Ce n’est que lorsque les vitesses deviennent très grandes (fractions non négligeables de la vitesse de la lumière) que cet étrange phénomène peut être observé et, même alors, seulement en utilisant des horloges extrêmement précises.
Pour voir comment cela pourrait fonctionner, considérons une « expérience de pensée » similaire à celle qu’Einstein a suggérée. (Il s’agit d’une expérience « pensée » plutôt que réelle car elle ne peut pas être réellement réalisée, comme vous vous en rendrez compte). Supposons que vous observiez l’horloge de Big Ben à travers un télescope très puissant, alors que vous vous en éloignez à bord d’un train très rapide qui est passé devant l’horloge à midi pile (je sais que les trains ne passent pas devant Big Ben, mais faisons semblant !) Si le train pouvait se déplacer à la vitesse de la lumière, que verriez-vous se passer avec les aiguilles de l’horloge ? Elles sembleraient rester immobiles, pointant toutes deux vers 12$ ! Pourquoi ? Parce que la lumière émise par (ou réfléchie par) les aiguilles à midi s’éloignerait de l’horloge à la même vitesse que vous dans le train, et la lumière émise plus tard ne pourrait pas rattraper le train ! Bizarre !
Vous voyez pourquoi il s’agit d’une « expérience de pensée » (en dehors du fait que les trains ne passent pas devant Big Ben) ? C’est parce qu’un train ne pourrait pas réellement se déplacer à la vitesse de la lumière (ce qui est une autre chose que la relativité restreinte nous dit – tout objet qui pèse quelque chose ne peut jamais se déplacer aussi vite que la lumière). Mais supposons que le train se déplace à la moitié de la vitesse de la lumière (toujours très rapide) – vous verriez les aiguilles de l’horloge bouger, mais plus lentement que celles de votre montre ! La mesure du temps dépend de la façon dont vous vous déplacez !
Comment est-ce possible ? Pour comprendre cela, considérons une sorte spéciale d’horloge, une horloge lumineuse . Il est peu probable que vous en trouviez une à côté de votre lit pour vous réveiller le matin. Elle consiste en une source de lumière qui émet des signaux qui parcourent une distance D et sont ensuite réfléchis vers la source. Le décalage ou l’intervalle de temps entre l’émission d’un signal et sa réception définit les tics de l’horloge ; ils sont espacés de $2T$, où \begin{equation} {T} = {D/c} \end{equation} avec $c$ représentant la vitesse de la lumière. (Rappelez-vous que vitesse = distance/temps, donc temps = distance/vitesse.)

Supposons maintenant qu’une fusée en mouvement transporte une telle horloge – l’expérience de l’équipage sera que les tics se produisent à des intervalles de $2T$. Supposons maintenant que l’équipage d’une fusée stationnaire observe l’horloge de la fusée en mouvement et la compare à la sienne, qui fait également tic-tac à intervalles de 2T$. Que verront-ils ? Les diagrammes ci-dessous devraient suggérer la réponse. (Je suis désolé que mes fusées ressemblent plus à des poissons !)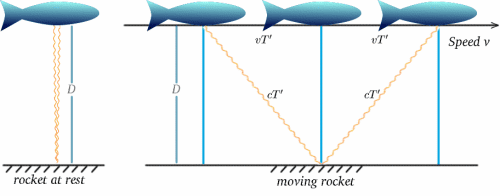
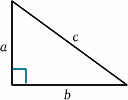
Pour la fusée en mouvement, la lumière est réfléchie par le miroir à mi-chemin entre le moment où le signal est envoyé et celui où il est réfléchi. Pour la fusée immobile, le temps de parcours semble être de $2T^{ \prime}$ disons. Nous pouvons calculer cela en utilisant un théorème très important (un nom fantaisiste pour quelque chose qui a été prouvé vrai en mathématiques !) – celui de Pythagore.

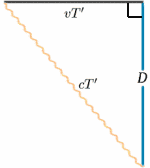\begin{equation} {a^2 + b^2} = {c^2} \quad (1) \end{equation} Dans le diagramme de la fusée, nous avons un triangle rectangle, donc \begin{equation} D^2 + v^2 T^{‘2} = {c^2 T ^{\prime 2}}\quad (2) \end{equation} Nous allons maintenant résoudre cette équation pour $T^{\prime}$ : \{begin{equation} {T^{prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \begin{equation} {T^{\prime 2} c^2 (1 – v^2/{c^2})} = {D^2} \quad (4),\end{equation} donnant \begin{equation} {T^{\prime}} = {\frac {D} {c \sqrt{(1 – v^2/{c^2})}}\quad (5) \end{equation} et donc \begin{equation} {T^{\prime}} = {\frac {T} {\sqrt{(1 – v^2/{c^2})}}, \quad (6) \end{equation} et les fréquences d’horloge seront différentes (sauf bien sûr $v=0$). En fait, $T^{\prime}$ est plus grand que $T$, donc il semble à l’équipage stationnaire que l’horloge en mouvement a des intervalles plus longs entre les tics et donc qu’elle va lentement.
Une fois que nous acceptons qu’il n’y a pas de définition universelle du temps qui tienne pour tout le monde, nous devons réfléchir à ce que nous entendons vraiment par mesurer le temps. Dans un certain sens, nous mesurons les distances le long de nos chemins dans l’espace-temps (repensez au diagramme espace-temps). Les jumeaux suivent des chemins différents dans l’espace-temps, il n’est donc pas si surprenant qu’ils aient connu des quantités de temps différentes.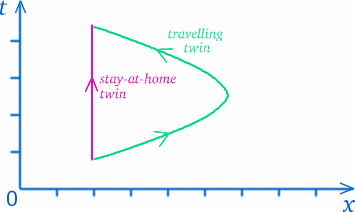
Mais ne tirez pas de conclusions hâtives – les choses ne sont pas toujours ce qu’elles semblent être… ! Le chemin de la jumelle voyageuse semble plus long mais cela signifie-t-il qu’elle a vécu plus de temps ? Pour vous rendre compte de la difficulté de ce genre de question, pensez à une situation qui pourrait être assez similaire. Supposons que vous habitiez à Trumpington, au sud de Cambridge, et que vous souhaitiez faire vos courses au Tesco à l’extrémité nord du centre-ville (autant que possible, en évitant les zones piétonnes), sur le périphérique ou sur la rocade – voir le schéma ci-dessous.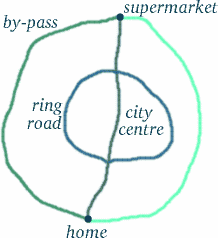
À la plupart des heures de la journée, vous constateriez que le trajet le plus long – la rocade – prend le moins de temps, suivi par le périphérique. Etes-vous maintenant convaincu que la réponse évidente n’est pas toujours la bonne ??
Nous avons vu comment le temps est mesuré à l’aide de signaux lumineux. Une fois que nous disposons d’une horloge précise, nous pouvons alors mesurer la distance en utilisant les signaux lumineux ou radar réfléchis par l’objet distant ; la distance sera égale à la moitié du temps de parcours de la lumière, multiplié par la vitesse de la lumière.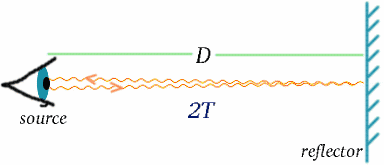

\begin{equation} {D} = {cT}\quad (7) \end{equation} Comme le temps, la distance est une grandeur où le résultat de la mesure dépend de la façon dont l’observateur se déplace.

Facteurs K

Je vais maintenant décrire une idée qui devrait nous aider à faire des calculs du type d’effet dont je vous ai parlé.
Supposons qu’un astronaute B (pour Ben) soit dans une fusée se déplaçant à la vitesse $c/5$ en s’éloignant d’un autre astronaute A (pour Alf) dans une station spatiale. Une fois par an, le 13 mars, Alf envoie des vœux d’anniversaire à Ben. Supposons que la station spatiale mesure la distance parcourue par le message radio transmettant ces vœux en 2010, soit une demi-année-lumière, pour atteindre la fusée, ce qui prend une demi-année. Le message suivant est envoyé exactement un an plus tard. Lorsque ce signal radio a parcouru une demi-année jusqu’à l’endroit où Ben l’astronaute a reçu le signal précédent, la fusée s’est déplacée d’un cinquième d’année-lumière plus loin, de sorte que ce signal doit voyager plus longtemps pour rattraper la fusée ; en fait, le temps mesuré par Alf lorsque le signal atteint la fusée est de trois quarts d’année après son envoi – voir le diagramme ci-dessous. Le pauvre Alf en conclut que les vœux d’anniversaire envoyés chaque année seront reçus par Ben à des intervalles d’un an et quart, selon l’horloge d’Alf.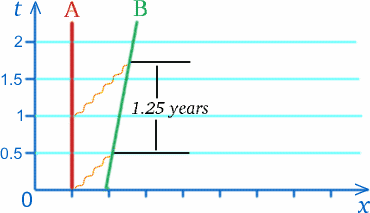
Cela ne nous dit pas ce que Ben mesurera pour ces intervalles, mais cela suggère que cela pourrait bien ne pas être une année ! Un effet similaire se produira pour les signaux envoyés de Ben à Alf.
Maintenant, examinons le cas général et rendons cela plus précis. Considérons deux observateurs Alf et Ben qui s’éloignent l’un de l’autre à des vitesses constantes.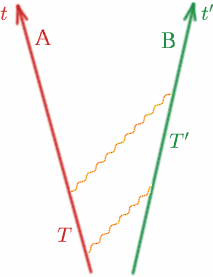
Alf envoie un signal lumineux puis un autre au temps $T$ plus tard. Ben reçoit les deux signaux à des instants $T^{\prime}$ d’écart, selon son horloge. On définit alors une quantité $K$ par \begin{equation} {K} = {T^{\prime}/T}. \quad (8) \end{equation} Notez que si Alf et Ben se déplaçaient à la même vitesse (dans la même direction !), $K$ serait égal à un. Nous verrons plus loin comment $K$ dépend de la vitesse relative d’Alf et de Ben. $K$ est parfois appelé le facteur de décalage Doppler et l’effet est similaire à celui des ondes sonores – vous devez tous connaître le changement de son de la sirène d’une ambulance ou d’une voiture de police lorsqu’elle s’approche puis s’éloigne.
Comment pouvons-nous mesurer $K$ ? La façon évidente est que les observateurs gardent des enregistrements du moment où les signaux lumineux sont envoyés et reçus afin qu’ils puissent calculer $T$ et $T^{\prime}$, et donc $K$, lorsqu’ils se rencontrent plus tard. Une autre possibilité serait que l’un dispose d’un télescope très puissant avec lequel il pourrait observer l’horloge de l’autre (c’est vraiment le train qui passe devant Big Ben qui recommence !).
Nous devons faire quelques hypothèses sur ce nombre $K$ pour qu’il nous soit utile. Nous supposons d’abord que lorsque Alf et Ben se déplacent à des vitesses constantes, alors $K$ ne dépend pas du moment où $T$ et $T^{\prime}$ sont mesurés, ni de la taille de $T$. Ainsi, par exemple, si Alf attend deux fois plus longtemps entre l’envoi de signaux lumineux, $K$ sera le même. Voyez si vous pouvez compléter les nombres$T_1^{\prime}$, $T_2^{\prime}$, $T_3^{\prime}$ dans ce cas.
?

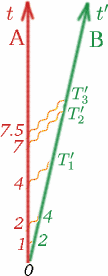
(Remarquez que l’on peut commencer à mesurer le temps lorsque les deux observateurs sont ensemble, et qu’ils peuvent tous deux mettre leurs chronomètres à zéro à ce moment-là). Donc, en général, nous avons
?

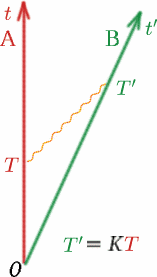
La deuxième chose que nous supposons, qui est tout aussi importante, est que le $K$ mesuré par Ben pour les signaux lumineux provenant de Alf est le même que celui mesuré par Alf pour les signaux lumineux provenant de Ben. Pourquoi supposer cela ? Imaginez deux voitures identiques dos à dos sur une route. La voiture $A$ reste immobile et la voiture $B$ s’éloigne de $A$ à une vitesse de $50km/hr$. Les passagers regardant par la vitre arrière de $A$ verront $B$disparaître à la vitesse appropriée. Les passagers de $B$ verront une image très similaire s’ils regardent par leur fenêtre arrière – la voiture $A$ semblera s’éloigner à la même vitesse ! Avez-vous déjà fait cette expérience étrange d’être assis dans un train et de penser qu’il vient de s’éloigner, alors qu’il s’avère que c’était le train voisin qui s’éloignait dans la direction opposée et que votre train est toujours stationnaire ?
Cette hypothèse permet à un observateur de mesurer $K$ par radar sans aucune coopération de l’autre. Quelqu’un peut-il deviner comment ? Laissez-moi vous donner un indice.
Supposons comme d’habitude qu’Alf et Ben s’éloignent l’un de l’autre à vitesse constante. Alf émet deux signaux à un intervalle de $T$, Ben les réfléchit à l’intervalle $T^{\prime}$ et Alf les reçoit à nouveau à l’intervalle $T^{\prime\prime}$. Comment Alf peut-il calculer $K$?
?

Réponse

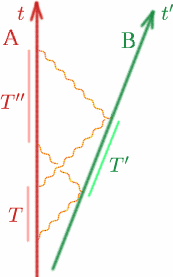
\begin{equation} {T^{\prime}} = {K T} \quad (9), \end{equation} \begin{equation} {T^{\prime}} = {K T^{\prime}}\quad (10) \end{equation} Donc \begin{equation} {T^{\prime\prime}} = {K(K T)} = {K^2 T}\quad (11) \end{equation} donc nous avons \begin{equation} {K} = {\sqrt{T^{\prime\prime}/T}. \quad (12) \end{equation} Problème Afin d’effectuer une manœuvre d’amarrage compliquée, il est essentiel que les deux vaisseaux spatiaux soient maintenus au repos l’un par rapport à l’autre. Concevez une expérience simple pour vérifier qu’il en est ainsi.

La relation entre K et la vitesse

Nous savons déjà que si la vitesse relative d’Alf et de Ben est nulle, alors $K$ = 1$. Quelle est sa valeur pour les vitesses générales ? Il existe un moyen astucieux de le déterminer, qui utilise l’idée dont nous venons de parler, plus l’idée de simultanéité. Qu’est-ce que cela signifie ? Je vais vous l’expliquer dans une minute.
D’abord, imaginons nos deux observateurs habituels qui s’éloignent l’un de l’autre avec une vitesse constante $v$. Supposons que lorsqu’ils sont ensemble, ils règlent tous deux leurs horloges sur $t = 0$. Au temps $T$ de son horloge, Alf émet un signal radio ; Ben le réfléchit au temps $T’$ de son horloge et Alf le reçoit à nouveau au temps $T^{\prime\prime}$ de son horloge. Faisons un dessin comme d’habitude.
?

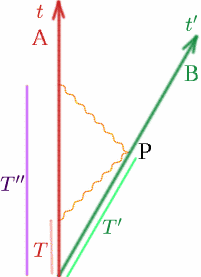
Nous savons maintenant que \begin{equation} {T^{\prime}} = {K T}\quad (13) \end{equation} \begin{equation} {T^{\prime}} = {K T^{\prime}} = {K^2 T}. \quad (14) \end{equation} Alf pense donc que le temps de parcours de l’impulsion radio est de \begin{equation} {T^{\prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{equation} et Alf calcule que la distance, $D$, entre lui et Ben, est la moitié de la distance parcourue par le signal radio, soit la moitié de la vitesse multipliée par le temps : \{begin{equation} {D} = {\frac {1} {2} c(K^2-1)T}. \quad (16) \end{equation} Nous savons maintenant que la distance entre Alf et Ben change constamment. Nous devons donc nous demander quand (c’est-à-dire à quel moment) cette distance entre Alf et Ben existe. C’est là que nous avons besoin de l’idée de simultanéité. La distance est clairement mesurée lorsque Ben se trouve au point $P$, mais à quel moment cela correspond-il pour Alf ? Eh bien, Alf sait que l’impulsion radio parcourt la même distance aller-retour, donc l’événement $Q$, qu’Alf juge être en même temps que $P$, sera à mi-chemin entre $T$ et $T^{\prime\prime}$. (Nous disons que $Q$ est simultané à $P$ pour Alf – cela signifie simplement en même temps). Donc le temps à $Q$ est \begin{equation} {T_Q} = {\frac {1} {2}(T+T »)} = {\frac {1} {2} (K^2+1)T}. \quad (17) \end{equation} Alf en conclut que Ben a parcouru une distance $D$ en un temps $T_Q$, sa vitesse $v$ est donc donnée par \begin{equation} {v} = {\frac {D} {T_Q}} = {\frac {\frac {1} {2} c(K^2-1)T} {frac {1}{2}} (K^2+1)T}}. \quad (18) \end{equation} Par conséquent, nous avons \begin{equation} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \quad (19) \end{equation} Nous pouvons maintenant calculer $K$ en fonction de $\frac {v} {c}$ : \begin{equation} {(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \end{equation} \begin{equation} {K^2 \frac{v}{c} + \frac{v}{c} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c}} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Donc \begin{equation} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}}\quad (23) \end{equation} et donc \begin{equation} {K} = \sqrt{{Gauche({\frac{1+\frac{v}{c}}{1-\frac{v}{c}}\droite)}}. \quad (24) \end{equation} Essayez de trouver quelques valeurs de K :
par exemple $v = c/4$ – cela donne $K = \sqrt{5/3} = 1,291$.
Essayez maintenant $v = c/2, 9c/10, 99c/100$.
Maintenant, peu importe que Alf soit immobile et Ben en mouvement ou l’inverse – $K$ reste le même. Ce qui est différent, c’est si Alf et Ben se rapprochent l’un de l’autre plutôt que de s’éloigner – dans ce cas, on prend la valeur de $v$ comme négative, mais on peut utiliser la même formule.
e.g. si Alf et Ben se rapprochent l’un de l’autre avec une vitesse relative de $c/2$, \begin{equation} K = \sqrt{{\gauche({\frac{1+(-1/2)}{1-(-1/2)}}\droite)}} = \sqrt{{\gauche({\frac{1/2}{3/2}\droite)}} = \sqrt{1/3}. \quad (25) \end{equation}. Calculons $K$ pour quelques vitesses typiques:
1) des avions de ligne se rapprochant l’un de l’autre avec une vitesse de 1000km/h$;
2) des galaxies de notre amas s’éloignant l’une de l’autre avec des vitesses relatives de 500km/s$;
3) une voiture s’approchant d’un policier à 100km/h$;
4) vous marchant vers votre ami à 5km/h$ Pensez-vous qu’un de ces effets serait observable ? Le paradoxe des jumeaux – enfin !
Que se passe-t-il ? Pourquoi est-ce un paradoxe ? (Que signifie le mot paradoxe d’ailleurs ?)
Préoccupons-nous de vraies jumelles, Albertina et Brigitta ! Albertina reste à la maison à Londres, tandis que Brigitta, l’aventurière, part en voyage dans l’espace. Elle s’éloigne de la Terre pendant 6 ans, mesurés par son horloge, dans un vaisseau spatial très rapide qui se déplace à $v = 4c/5$. Elle revient ensuite à la même vitesse pendant 6 ans. Brigitta mesure donc un temps de 12 ans pour son voyage – elle a 12 ans de plus lorsqu’elle rentre chez Albertina à Londres. Mais de combien Albertina est-elle plus âgée ? Voyons si votre supposition était juste ou peut-être juste proche !
Dessinons un diagramme espace-temps :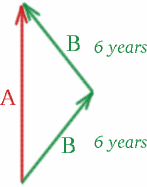
Lors du voyage aller de Brigitta, les jumeaux s’éloignent l’un de l’autre avec une vitesse relative $v = 4c/5$, donc \begin{equation} {K^2} = {\frac{1+\frac{4}{5}}{1-\frac{4}{5}} = {9}, \quad (26) \end{equation} et nous avons $K=3$. Sur le chemin du retour de Brigitta, elles se rapprochent l’une de l’autre avec la même vitesse, donc \begin{equation} {K^2} = {\frac{1-\frac{4}{5}}{1+\frac{4}{5}}\quad (27) \end{equation} et $K=1/3$. Tout ce dont nous avons besoin pour calculer le temps que mesure Albertina est de mettre un signal lumineux ! Une suggestion où ?
Supposons qu’Albertina envoie un signal au point $S$, choisi de façon à ce qu’il atteigne Brigitta à $U$, au moment où elle s’apprête à faire demi-tour.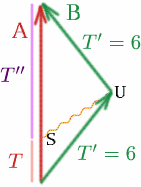
Alors que vaut $T$ si $T^{\prime}=6$ et $K=3$ ? Nous avons \begin{equation} {T^{\prime}} = {K T} \quad (28) \end{equation}
donc $6=3T$ et $T=2$.
Regardons maintenant ce qui se passe lors du voyage de retour de Brigitta. Combien vaut $T^{\prime\prime}$ ? Nous avons $T^{\prime}=6$, $K=1/3$ et \Nquad (29) \Nquad (29) \Nequad (29) \Nquad (29) \Nquad (29) \Nquad (29) \Nquad (29) \Nquad (29) \Nquad (29) \Ndonc $6=T^{\prime\prime}/3$ et $T^{\prime\prime}=18$. Par conséquent, le temps total mesuré par Albertina est de $T+T^{\prime\prime}=20$ ans, elle a donc 20 ans de plus lorsqu’elles se rencontrent, alors que Brigitta n’a que 12 ans de plus ! Albertina a donc vieilli de 8 ans de plus que Brigitta!
Vous avez donc bien deviné????
Ce que vous pouvez essayer de faire par vous-même, ce sont des expériences avec les nombres. Par exemple, vous pouvez imaginer que Brigitta entreprend un voyage de 10+10=20$ ans, et vous pouvez déterminer à quelle vitesse elle doit voyager pour qu’Albertina n’ait vieilli que d’un an de plus qu’elle (c’est-à-dire que 21$ ans se sont écoulés sur l’horloge d’Albertina) lorsque Brigitta revient. Peut-être pouvez-vous déterminer s’il serait possible qu’il y ait un voyage spatial réaliste (c’est-à-dire réalisable) au cours duquel les jumeaux vieilliraient différemment d’une quantité notable !
Pourquoi tout cela est-il appelé un paradoxe ? Rappelez-vous ce que signifie un paradoxe ? Nous avons dit précédemment que si deux personnes se déplacent à des vitesses constantes (et donc des vitesses constantes l’une par rapport à l’autre), une grande partie de ce qui se passe est la même, que l’on considère la première immobile et la seconde en mouvement, ou l’inverse. Si l’on applique cet argument à Albertina et Brigitta, pourquoi ne pas considérer que Brigitta, dans son vaisseau spatial, est la personne immobile, et qu’Albertina, sur Terre, s’éloigne et revient. Dit comme cela, cela semble plutôt stupide, mais j’espère que vous comprenez l’idée. On pourrait donc s’attendre à ce que Brigitta soit plus âgée qu’Albertina lorsqu’elles se rencontrent enfin. Mais nous avons déjà dit qu’Albertina est alors plus âgée. Comment ces deux affirmations peuvent-elles être vraies ? C’est le paradoxe !
Vous voyez ce qui ne va pas ? ??
Le point est que Brigitta ne se déplace pas à une vitesse constante par rapport à Albertina pendant tout son voyage ; elle a deux longues sections de voyage dans lesquelles elle le fait, mais entre les deux il y a une section peut-être courte mais très importante où elle décélère, s’arrête et ensuite accélère dans la direction opposée. C’est ce qui fait toute la différence ! L’accélération est un phénomène réel, comme vous le savez probablement grâce aux manèges qui vous rendent malade à la foire ! Savez-vous comment on peut le détecter avec un simple équipement ?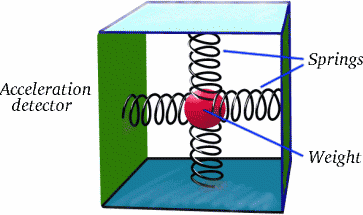
Alors, que pensez-vous de tout cela ? Il semble un peu injuste que Brigitta puisse voyager et voir plus de l’Univers mais qu’elle se retrouve plus jeune que sa sœur jumelle restée à la maison – la vie ne semble pas toujours juste ! Mais cela devrait vous encourager à voyager – pas nécessairement dans l’espace ! – et à être aventureux ! Référence Pour en savoir plus sur le paradoxe des jumeaux et les techniques décrites ici, vous pouvez consulter le livre Flat and Curved Space-Times, de G. F. R. Ellis et moi-même (publié par Oxford University Press en 1988). Vous pouvez également regarder les livres de M. Tompkins qui présentent les concepts de la relativité restreinte d’une manière amusante et abordable.

Vous pouvez trouver des critiques des livres de M. Tompkins et les commander sur le site de Cambridge University Press, par exemple voir Le nouveau monde de M. Tompkins : le classique M. Tompkins de George Gamow en livre de poche

.