Introducción

¡Si sigue este proyecto, llegará a una conclusión sorprendente! Supongamos que uno de un par de gemelos idénticos realiza un viaje al espacio y luego regresa para comparar su edad (digamos la de ella) con la del otro gemelo que ha permanecido en el mismo lugar de la Tierra. Resulta que, tras el viaje, ¡una de las gemelas será más joven que su hermana! Te estarás preguntando cómo es posible, y el objetivo de este proyecto es mostrarte cómo.
Empecemos por jugar a un juego de adivinanzas: ¡descubriremos si has acertado al final! Supongamos que la gemela viajera realiza un viaje de 12 años: 6 de ida y 6 de vuelta. Evidentemente, a la vuelta tendrá 12 años más. ¡Lo que tienes que hacer es adivinar cuántos años tendrá el gemelo que no viaja….! Tengo que decirte a qué velocidad viaja el gemelo que se desplaza, digamos que a cuatro quintos de la velocidad de la luz, aunque me atrevo a decir que esto no te ayudará demasiado a adivinar. Permítanme sugerirles que adivinen un número entero entre 1 y 30!
Antes de considerar los gemelos, debemos establecer ciertas herramientas que necesitaremos para entender lo que está sucediendo. Utilizaremos mucho un tipo de gráfico llamado diagrama espacio-temporal. No te preocupes si nunca has utilizado gráficos, intentaremos empezar por lo más básico.

Gráficos

El tipo de gráfico más sencillo es simplemente una imagen de lo que ocurre en una superficie plana elegida. Supongamos que estás sentado en una mesa o un escritorio y que tienes dos reglas y una hoja de papel grande. Empezando por la esquina inferior izquierda, coloca una regla a lo largo de la parte inferior y otra en el lado izquierdo, con el papel en posición intermedia. El resultado debería ser el siguiente:

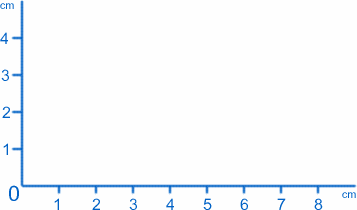
Llamamos al punto donde se encuentran las dos reglas (el cero en ambas escalas) el origen, o O para abreviar, y las reglas proporcionan los dos ejes . Siguiendo la convención, llamaremos eje x al que está en la parte inferior, y eje y al que está en la parte superior. Podemos etiquetar cualquier punto del papel por sus valores de $x$ e $y$.Por ejemplo, el origen tiene $x=0$, $y=0$. El punto a 1 cm$ del eje y y a 2 cm$ del eje x tiene $x=1$, $y=2$ (¡realmente los tengo al revés!).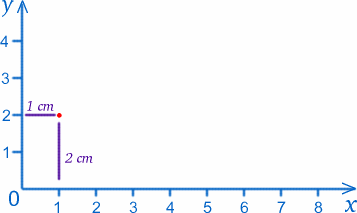

Ejercicio Dibuja tu propia gráfica y marca los siguientes puntos:
$x=3$, $y=0$;
$x=2$, $y=1$;
$x=3$, $y=2$;
$x=4$, $y=1$.
¿Qué forma tienen? Supongamos que una camina por el papel manteniéndose siempre a una distancia de $1cm$ del eje x. Su trayectoria sería una línea, descrita por la ecuación $y=1$ (una forma elegante de decir lo que se dice con palabras en la frase anterior). Otra podría caminar siempre a 3 cm$ del eje y; la ecuación de su trayectoria sería $x=3$. Una hormiga algo más original podría caminar de forma que su distancia a ambos ejes fuera siempre la misma; pasaría por $x=1$, $y=1$; $x=2$, $y=2$; etc y su trayectoria vendría dada por la ecuación $x=y$.

Diagramas espacio-temporales

En este apartado dibujaremos algunas gráficas de aspecto muy similar a las del apartado anterior, pero su significado será bastante diferente. Seguimos teniendo dos ejes, y el etiquetado como $x$ sigue representando la distancia en una determinada dirección. Sin embargo, el que estaba etiquetado como $y$ ahora está etiquetado como $t$, que representa el tiempo, medido en segundos, por ejemplo. Supongamos ahora que la pelota rueda a lo largo de una trayectoria recta; entonces los puntos de la gráfica corresponderían a las posiciones de la pelota en momentos determinados, por ejemplo, $x=5$, $t=4$ corresponderían a que la pelota se encuentra a 5cm$ del origen 4$ segundos después de iniciada la medición del tiempo.
Ejercicio Traza los puntos de la gráfica correspondientes a los siguientes sucesos en la historia de la pelota: $x=4$, $t=1$; $x=4$, $t=2$; $x=4$, $t=3$. ¿Cómo interpretarías esto?
Ahora prueba con $x=1$, $t=1$; $x=3$, $t=2$; $x=5$, $t=3$. ¿Qué notas en estos puntos?
Si la trayectoria de la bola es una línea recta en la gráfica, significa que la bola se mueve con velocidad constante (quizás velocidad cero). En ese caso podemos calcular la velocidad viendo la distancia que recorre la pelota en un segundo: dividimos el cambio en el valor x por el correspondiente cambio en el valor t. Así, en nuestro segundo ejemplo, la velocidad de la pelota es de 2 cm/seg$. ¿Estás de acuerdo?
Ejercicio Dibuja una gráfica que represente el movimiento de una pelota que se mueve hacia delante y hacia atrás entre dos puntos, con velocidad constante (pero cambiando periódicamente de dirección, por supuesto).
Ahora vamos a hacer algo bastante extraño con nuestra gráfica. En la teoría llamada relatividad especial , que es la que hace interesante pensar en los gemelos y en los viajes espaciales, a menudo necesitamos trazar rayos de luz en nuestras gráficas. Ahora bien, los rayos de luz viajan en el espacio vacío con una velocidad constante y muy grande (pero finita); un rayo de luz que llega a ti desde el sol salió de allí hace unos 8$ minutos. (La gente solía creer que la luz viajaba infinitamente rápido, de modo que podías ver las estrellas en el momento en que las observabas, pero ahora se sabe que esto es falso). Para ser más precisos, ¡la velocidad de la luz es de unos $30000000000cm/seg$! Esto podría dar lugar a escalas muy extrañas en los ejes de una gráfica espacio-temporal, así que optaremos por medir la distancia de otra manera; las unidades en el eje x serán segundos-luz, es decir, la distancia recorrida por la luz en un segundo. (Si la escala para $t$ es de años, la escala x correspondiente será de años-luz).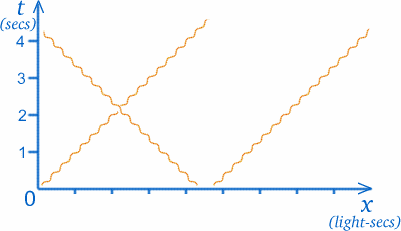
La gran ventaja de esto es que la trayectoria de un rayo de luz siempre estará a $45$ grados respecto a los ejes. Esto significa que un rayo de luz que pase por O formará ángulos iguales con respecto a ambos ejes, como se ve en el diagrama. (Aunque la luz viaja a velocidad constante, por lo que su trayectoria es una línea recta, la representamos con una línea ondulada, como se muestra, para distinguir los rayos de luz de las trayectorias de otros objetos con masa.)
?

Medir el tiempo

Tendemos a suponer que cuando la gente no está de acuerdo con la hora que es, ¡el reloj de alguien está equivocado, o tal vez las personas están en diferentes zonas horarias! Pero es incluso más complicado que eso. Según la relatividad especial, dos personas pueden estar en el mismo lugar y correlacionar sus relojes, pero si una se mueve con respecto a la otra, posteriormente discreparán sobre la hora que es.Desgraciadamente, si te asocias con un amigo e intentas poner a prueba esta teoría, te llevarás una decepción, no porque la teoría sea errónea, sino porque a la velocidad a la que probablemente puedas correr, incluso si eres un superatleta, el efecto será demasiado pequeño para observarlo. Sólo cuando las velocidades se vuelven muy grandes (fracciones considerables de la velocidad de la luz) se puede observar este extraño fenómeno e, incluso entonces, sólo utilizando relojes extremadamente precisos.
Para ver cómo podría funcionar esto, consideremos un «experimento mental» similar a uno que sugirió Einstein. (Se trata de un experimento «pensado» y no real porque no se puede realizar realmente, como se dará cuenta). Supongamos que observamos el reloj del Big Ben a través de un telescopio muy potente, mientras nos alejamos de él en un tren muy rápido que pasa por delante del reloj exactamente al mediodía (ya sé que los trenes no pasan justo por delante del Big Ben, ¡pero imaginemos!). Ahora bien, si el tren pudiera moverse a la velocidad de la luz, ¿qué verías que le ocurre a las agujas del reloj? ¡Parecerían estar paradas, ambas apuntando a $12$! ¿Por qué? Porque la luz emitida (o reflejada) por las agujas al mediodía se alejaría del reloj exactamente a la misma velocidad que tú en el tren, y la luz emitida en momentos posteriores no podría alcanzar al tren. ¿Raro!
¿Puedes ver por qué esto es un «experimento mental» (aparte del hecho de que los trenes no pasan por delante del Big Ben)? Es porque un tren no podría moverse realmente con la velocidad de la luz (que es otra cosa que nos dice la relatividad especial: cualquier objeto que pese algo nunca puede moverse tan rápido como la luz). Pero supongamos que el tren se desplaza a la mitad de la velocidad de la luz (que sigue siendo muy rápida): veríamos que las agujas del reloj se mueven, ¡pero más lentamente que las de nuestro reloj! La medición del tiempo depende de la forma en que te muevas
¿Cómo puede ser esto? Para entenderlo, consideremos un tipo especial de reloj, un reloj de luz. No es probable que encuentre uno de ellos al lado de su cama despertándole por la mañana. Consiste en una fuente de luz que emite señales que recorren una distancia D y luego se reflejan en la fuente. El espacio de tiempo o intervalo entre cada vez que se emite una señal y cuando se recibe de vuelta, define los ticks del reloj; se producen con un intervalo de $2T$, donde \begin{equation} {T} = {D/c} \con $c$ representando la velocidad de la luz. (Recordemos que la velocidad = distancia/tiempo, por lo que el tiempo = distancia/velocidad.)

Supongamos ahora que un cohete en movimiento lleva un reloj de este tipo: la experiencia de la tripulación será que los ticks se producen a intervalos de $2T$. Supongamos ahora que la tripulación de un cohete estacionario observa el reloj del cohete en movimiento y lo compara con el suyo propio, que también hace tictac a intervalos de $2T$. ¿Qué verán? Los siguientes diagramas deberían sugerir la respuesta. (¡Lamento que mis cohetes se parezcan más a un pez!)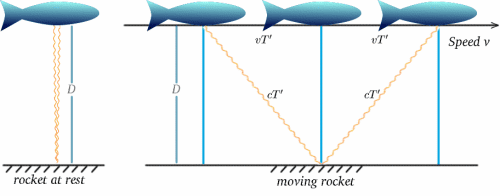
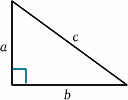
Para el cohete en movimiento, la luz se refleja en el espejo en el tiempo medio entre el envío de la señal y su reflejo. Desde el cohete estacionario, el tiempo de viaje parece ser $2T^{ \prime}$ digamos. Podemos calcular esto utilizando un teorema muy importante (¡un nombre elegante para algo que se ha demostrado que es cierto en matemáticas!): el de Pitágoras.

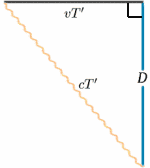{comenzar{ecuación} {a^2 + b^2} = {c^2} \quad (1) \quad{equation} En el diagrama del cohete, tenemos un triángulo rectángulo, por lo que \begin{equation} D^2 + v^2 T^{‘2} = {c^2 T ^{{prime 2}}quad (2) \end{equation} Ahora resolvemos esto para $T^{{prime}$: \begin{equation} {T^{prime 2} (c^2 – v^2)} = {D^2}, \quad (3) \end{equation} \Inicio{ecuación} {T^{prima 2} c^2 (1 – v^2/{c^2})} = {D^2} \(4), finalizando la ecuación, dando comienzo a la ecuación de T^^prime} = {frac {D} (5) y, por tanto, \begin{equation} {T^{prime}} = {\frac {T} {\sqrt{1 – v^2/{c^2}}, \quad (6) \end{equation} y las velocidades de reloj serán diferentes (a menos que, por supuesto, $v=0$). De hecho, $T^{\prime}$ es mayor que $T$, por lo que a la tripulación estacionaria le parece que el reloj en movimiento tiene intervalos más largos entre las pulsaciones y, por tanto, va más lento.
Una vez que aceptamos que no hay una definición universal del tiempo que valga para todo el mundo, tenemos que pensar qué entendemos realmente por medir el tiempo. En cierto sentido, estamos midiendo distancias a lo largo de nuestras trayectorias en el espacio-tiempo (pensemos en el diagrama espacio-tiempo). Los gemelos siguen caminos diferentes en el espacio-tiempo, por lo que no es tan sorprendente que hayan experimentado cantidades diferentes de tiempo.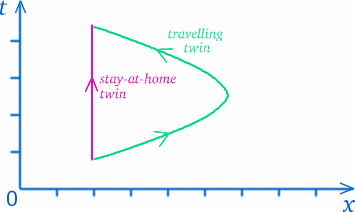
Pero no saques conclusiones precipitadas: ¡las cosas no son siempre lo que parecen…! El camino de la gemela viajera parece más largo, pero ¿significa eso que ha experimentado más tiempo? Para ver lo complicado que es este tipo de preguntas, piensa en una situación que podría ser bastante similar. Supongamos que usted vive en Trumpington, en la parte sur de Cambridge, y quiere ir a comprar a Tesco’s en el extremo norte del centro de la ciudad (lo más cerca posible, evitando las zonas peatonales), en la carretera de circunvalación o en la circunvalación – véase el diagrama siguiente.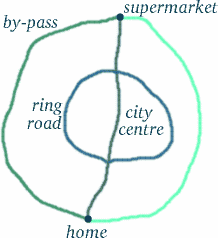
En la mayoría de los momentos del día, la ruta más larga -la circunvalación- es la que menos tiempo requiere, seguida de la circunvalación. ¿Estás convencido de que la respuesta obvia no siempre es la correcta?
Hemos visto cómo se mide el tiempo utilizando señales luminosas. Una vez que tenemos un reloj preciso, podemos medir la distancia utilizando las señales de luz o de radar reflejadas por el objeto distante; la distancia será la mitad del tiempo de viaje de la luz, multiplicado por la velocidad de la luz.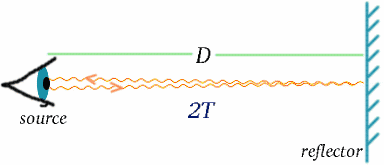

{comienza}{ecuación} {D} = {cT}{cuadrado} (7) {comienza}. Al igual que el tiempo, la distancia es una magnitud en la que el resultado de la medición depende de la forma en que se mueve el observador.

Factores K

Ahora voy a describir una idea que debería ayudarnos a hacer cálculos del tipo de efecto que os he estado contando.
Supongamos que un astronauta B (por Ben) está en un cohete alejándose a la velocidad $c/5$ de otro astronauta A (por Alf) en una estación espacial. Una vez al año, el 13 de marzo, Alf envía una felicitación de cumpleaños a Ben. Supongamos que el mensaje de radio que lleva esta felicitación en el año 2010 es medido por la estación espacial para recorrer una distancia de medio año luz para llegar al cohete, tardando medio año en hacerlo. El siguiente mensaje se envía exactamente un año después. Cuando esta señal de radio ha viajado durante medio año hasta el lugar donde Ben recibió la señal anterior, el cohete se ha movido una quinta parte de un año luz más allá, por lo que esta señal tiene que viajar durante más tiempo para alcanzar al cohete; de hecho, el tiempo medido por Alf cuando la señal llega al cohete es tres cuartos de año después de haber sido enviada – véase el diagrama de abajo. El pobre Alf concluye que las felicitaciones de cumpleaños enviadas anualmente serán recibidas por Ben a intervalos de un año y cuarto, según el reloj de Alf. ¡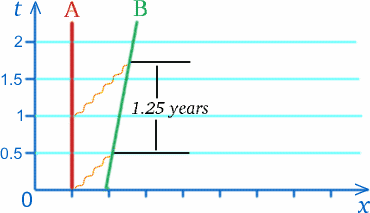
Esto no nos dice lo que Ben medirá para estos intervalos, pero sí sugiere que bien podría no ser un año! Un efecto similar ocurrirá para las señales enviadas de Ben a Alf.
Ahora veamos el caso general y hagamos esto más preciso. Consideremos dos observadores Alf y Ben que se alejan el uno del otro a velocidades constantes.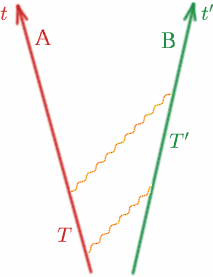
Alf envía una señal luminosa y otra en el tiempo $T$ posterior. Ben recibe las dos señales a tiempos $T^{\prime}$ de distancia, según su reloj. Entonces definimos una cantidad $K$ mediante la \Necuación {K} = {T^{prime}/T}. \(8) \N – fin{ecuación} Nótese que si Alf y Ben se movieran con la misma velocidad (¡en la misma dirección!), $K$ sería uno. Veremos más adelante cómo depende $K$ de la velocidad relativa de Alf y Ben. A $K$ se le llama a veces factor de desplazamiento Doppler y el efecto es similar al de las ondas sonoras: todos debéis conocer el cambio de sonido de la sirena de una ambulancia o de un coche de policía cuando se acerca y se aleja.
¿Cómo podemos medir $K$? La forma obvia es que los observadores lleven un registro de cuándo se envían y reciben las señales luminosas para poder calcular $T$ y $T^{{prime}$, y por tanto $K$, cuando se encuentren más tarde. Otra posibilidad sería que uno de ellos tuviera un telescopio muy potente con el que pudiera observar el reloj del otro (¡esto sí que es volver a pasar el tren por delante del Big Ben!).
Tenemos que hacer algunas suposiciones sobre este número $K$ para que nos sea útil. Suponemos en primer lugar que cuando Alf y Ben se mueven con velocidades constantes, entonces $K$ no depende de cuándo se miden $T$ y $T^{{prime}$, ni depende de lo grande que sea $T$. Así, por ejemplo, si Alf espera el doble de tiempo entre el envío de señales luminosas, $K$ será el mismo. A ver si puedes completar los números$T_1^{{prime}$, $T_2^{{prime}$, $T_3^{{{prime}$ en este caso.
?

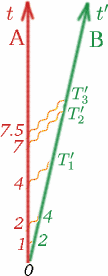
(Fíjate que está bien empezar a medir el tiempo cuando los dos observadores están juntos, y ambos pueden poner sus cronómetros a cero en ese momento). Así que en general tenemos
?

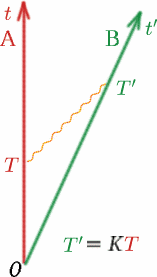
La segunda cosa que suponemos, que es igualmente importante, es que el $K$ medido por Ben para las señales luminosas de Alf es el mismo que el medido por Alf para las señales luminosas de Ben. ¿Por qué suponemos esto? Imagina dos coches idénticos uno detrás de otro en una carretera. El coche $A$ se queda quieto y el coche $B$ se aleja a 50km/h$ de $A$. Los pasajeros que miren por la ventanilla trasera de $A$ verán a $B$desaparecer a la velocidad correspondiente. Los pasajeros de $B$ verán una imagen muy similar si miran por su ventanilla trasera: ¡el coche $A$ parecerá alejarse a la misma velocidad! ¿Has tenido alguna vez la extraña experiencia de estar sentado en un tren y pensar que se acaba de alejar, cuando resulta que era el tren vecino el que se alejaba en dirección contraria y tu tren sigue estacionario?
Esta suposición hace posible que un observador mida $K$ por radar sin ninguna cooperación del otro. ¿Puede alguien adivinar cómo? Déjenme darles una pista.
Supongamos como siempre que Alf y Ben se separan con velocidad constante. Alf envía dos señales en un intervalo de $T$, Ben las refleja en el intervalo $T^{{prime}$ y Alf las recibe de nuevo en el intervalo $T^{{prime}$. ¿Cómo puede Alf calcular $K$?
?

Responde

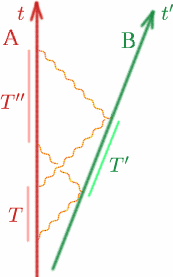
{comienza la ecuación} {T^{prime}} = {K T} \(9), fin de la ecuación. \Inicio {ecuación} {T^{prima}} = {K T^{prima}} {cuadrado (10). Por lo tanto \begin{equation} {T^{prime{prime}} = {K(K T)} = {K^2 T}\quad (11) \end{equation} por lo que tenemos \begin{equation} {K} = {\sqrt{T^{prime{prime}/T}. \(12) \N – fin{ecuación} Problema Para realizar una complicada maniobra de acoplamiento, es imprescindible que dos naves espaciales se mantengan en reposo una respecto de la otra. Diseña un experimento sencillo para comprobar que esto es así.

La relación entre K y la velocidad

Ya sabemos que si la velocidad relativa de Alf y Ben es nula, entonces $K$ = $1$. ¿Cuál es su valor para las velocidades generales? Hay una forma inteligente de resolverlo, que utiliza la idea de la que acabamos de hablar, más la idea de simultaneidad. ¿Qué significa eso? Lo explicaré en un minuto.
Primero imaginemos nuestros dos observadores habituales que se alejan el uno del otro con velocidad constante $v$. Supongamos que cuando están juntos, ambos ponen sus relojes a $t = 0$. En el tiempo $T$ de su reloj, Alf emite una señal de radio; Ben la refleja en el tiempo $T’$ de su reloj y Alf la recibe de nuevo en el tiempo $T^{\prime\prime}$ de su reloj. Hagamos un dibujo como de costumbre.
?

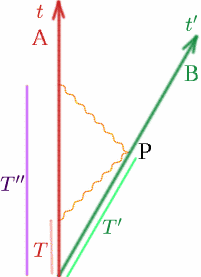
Ahora sabemos que \Ncomienza{ecuación} {T^{prime}} = {K T}{cuadro} (13) \N-end{ecuación} \ {comienzo{ecuación} {T^{prima{prima}} = {K T^{prima}} = {K^2 T}. \(14) \N – fin{ecuación} Así que Alf piensa que el tiempo de viaje del pulso de radio es \begin{equation} {T^{prime\prime}-T} = {K^2 T-T} = {(K^2-1)T}, \quad (15) \end{equation} y Alf calcula que la distancia, $D$, entre él y Ben, es la mitad de la distancia recorrida por la señal de radio , que es la mitad de la velocidad por el tiempo: \D = 1. {2} c(K^2-1)T}. \quad (16) \quad{ecuación} Ahora sabemos que la distancia entre Alf y Ben cambia constantemente, por lo que tenemos que preguntar cuándo (es decir, en qué momento) es la distancia entre Alf y Ben. Aquí es donde necesitamos la idea de la simultaneidad. La distancia se mide claramente cuando Ben está en el punto $P$, pero ¿a qué hora corresponde esto para Alf? Pues bien, Alf sabe que el pulso de radio recorre la misma distancia de ida y vuelta, por lo que el suceso $Q$, que Alf juzga que está en el mismo momento que $P$, estará a mitad de camino entre $T$ y $T^{prime\prime}$. (Decimos que $Q$ es simultáneo con$P$ para Alf -sólo significa al mismo tiempo). Así que el tiempo en $Q$ es \begin{equation} {T_Q} = {\frac {1} {2}(T+T»)} = {\frac {1} {2} (K^2+1)T}. \(17) \N – fin {ecuación} Así, Alf concluye que Ben ha recorrido una distancia $D$ en un tiempo $T_Q$, por lo que su velocidad $v$ viene dada por \begin{equation} {v} = {\frac {D} {T_Q}} = {\frac {\frac {1} {2} c(K^2-1)T} {\frac {1}{2} (K^2+1)T}}. \(18) \ ~ – fin {ecuación} Por lo tanto tenemos \begin{equation} {\frac {v} {c}} = {\frac {K^2-1} {K^2+1}}. \(19) \frac {equation} Ahora podemos calcular $K$ en términos de $\frac {v} {c}$: \(K^2+1)\frac {v} {c}} = {K^2-1}, \quad (20) \frac {equation} \Inicio{ecuación} {K^2{frac{v}{c} + \frac{v}{c} = {K^2-1}, \quad (21) \end{equation} \begin{equation} {1+ \frac{v}{c} ={K^2(1- \frac{v}{c})}, \quad (22) \end{equation} Por lo tanto, \begin{equation} {K^2} = {\frac {1+ \frac{v}{c}} {1- \frac{v}{c}} {cuadrado (23) \final{ecuación} y por lo tanto \begin{ecuación} {K} = \frac{1+\frac{v}{c}}{1-\frac{v}{c}}{derecho}}. \(24) \ ~ – fin {ecuación} Intenta calcular algunos valores de K:
por ejemplo, $v = c/4$ – eso da $K = \sqrt{5/3} = 1,291$.
Ahora prueba $v = c/2, 9c/10, 99c/100$.
Ahora no importa si Alf está quieto y Ben se mueve o al revés – $K$ sigue siendo el mismo. Lo que es diferente es si Alf y Ben se están acercando el uno al otro en lugar de alejarse – en ese caso, tomamos el valor de $v$ para ser negativo, pero podemos utilizar la misma fórmula.
por ejemplo, si Alf y Ben se acercan el uno al otro con la velocidad relativa $c/2$, \begin{equation} K = \sqrt{{izquierda({\frac{1+(-1/2)}{1-(-1/2)}} {derecha)}} = \sqrt{{izquierda({\frac{1/2}{3/2} {derecha)}} = \sqrt{1/3}. \(25) \quad. Calculemos $K$ para algunas velocidades típicas:
1) aviones que se acercan con una velocidad de 1000km/h$;
2) galaxias de nuestro cúmulo que se alejan con velocidades relativas de 500km/s$;
3) un coche que se acerca a un policía a 100km/h$;
4) tú caminando hacia tu amigo a 5km/h$ ¿Crees que alguno de estos efectos sería observable? La paradoja de los gemelos – ¡por fin!
¿Qué ocurre? ¿Por qué es una paradoja? (¿Qué significa la palabra paradoja?)
Consideremos a dos gemelas idénticas, Albertina y Brigitta. Albertina se queda en casa en Londres, mientras que Brigitta, la aventurera, se va de viaje al espacio. Se aleja de la Tierra durante 6 años, medidos por su reloj, en una nave espacial muy rápida que viaja a $v = 4c/5$. Luego regresa a la misma velocidad durante 6 años. Por tanto, Brigitta mide un tiempo de 12 años en su viaje, es decir, es 12 años mayor cuando vuelve a casa de Albertina en Londres. Pero, ¿cuántos años tiene Albertina? Veamos si tu suposición era correcta o tal vez se aproxima a ella
Dibujemos un diagrama espacio-temporal: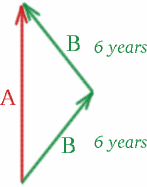
En el viaje de ida de Brigitta, las gemelas se separan con una velocidad relativa $v = 4c/5$, por lo que \begin{equation} {K^2} = {\frac{1+\frac{4}{5}{1-\frac{4}{5}} = {9}, \quad (26) \end{equation} y tenemos $K=3$. En el viaje de vuelta de Brigitta, se acercan con la misma velocidad, por lo que \begin{equation} {K^2} = {\frac{1-\frac{4}{5}{1+\frac{4}{5}{quad (27) \end{equation} y $K=1/3$. Lo único que tenemos que hacer para calcular el tiempo que mide Albertina es poner una señal luminosa. ¿Alguna sugerencia de dónde?
Supongamos que Albertina envía una señal en el punto $S$, elegido de forma que llegue a Brigitta en $U$, justo cuando está a punto de dar la vuelta.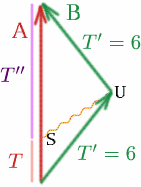
¿Cuál es entonces $T$ si $T^{{prime}=6$ y $K=3$? Tenemos \Nque empezar{ecuación} {T^{prima}} = {K T} (28) \\N – fin{ecuación}
por lo que $6=3T$ y $T=2$.
Ahora mira lo que pasa en el viaje de vuelta de Brigitta. ¿Qué es $T^{prime\}$? Tenemos que $T^{prime}=6$, $K=1/3$ y \begin{equation} {T^{prime}} = {K T^{prime\prime}}, \quad (29) \end{equation} por lo que $6=T^{prime\prime}/3$ y $T^{prime\prime}=18$. Por lo tanto, el tiempo total medido por Albertina es $T+T^{prime\prime}=20$ años, por lo que tiene 20 años más cuando se encuentran, mientras que Brigitta sólo tiene 12 años más. Así que Albertina ha envejecido 8 años más que Brigitta!
Así que ¿has adivinado bien????
Lo que puedes intentar hacer por tu cuenta son algunos experimentos con números. Por ejemplo, puedes imaginar que Brigitta hace un viaje de 10+10=20$ años, por ejemplo, y puedes calcular a qué velocidad tiene que viajar para que Albertina haya envejecido sólo un año más que ella (es decir, que hayan pasado 21$ años en el reloj de Albertina) cuando Brigitta regrese. Tal vez puedas averiguar si es posible que haya un viaje espacial realista (es decir, realizable) en el que los gemelos envejezcan de forma diferente por una cantidad notable!
¿Pero por qué todo esto se llama paradoja? ¿Recuerdas lo que significa paradoja? Dijimos antes que si dos personas se mueven con velocidades constantes (y, por tanto, con velocidades constantes la una respecto a la otra), mucho de lo que ocurre es lo mismo si consideramos a la primera inmóvil y a la segunda en movimiento, o al revés. Aplicando este argumento a Albertina y Brigitta, ¿por qué no podemos considerar a Brigitta en su nave espacial como la persona que se queda quieta, y a Albertina en la Tierra que se aleja y vuelve? Dicho así, parece una tontería, pero espero que se entienda la idea. Entonces esperaríamos que Brigitta fuera mayor que Albertina cuando finalmente se encuentren. Pero ya hemos dicho que Albertina es mayor entonces. ¿Cómo pueden ser ciertas ambas afirmaciones? La cuestión es que Brigitta no se mueve a velocidad constante con respecto a Albertina en todo su viaje; tiene dos largos tramos de viaje en los que lo hace, pero entre ellos hay un tramo posiblemente corto pero muy importante en el que decelera, se detiene y luego acelera en sentido contrario. La aceleración es un fenómeno real, como probablemente sepas por las atracciones que te hacen sentir mal en una feria. ¿Sabes cómo se puede detectar con un simple equipo?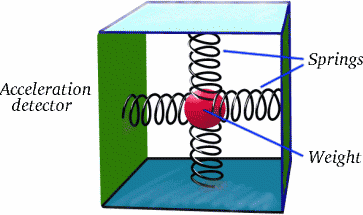
¿Qué opinas de todo esto? Parece un poco injusto que Brigitta pueda viajar y ver más del Universo pero acabe siendo más joven que su hermana gemela que se queda en casa: ¡la vida no siempre parece justa! Pero debería animarte a viajar -¡no necesariamente al espacio! – y a ser aventurero. Referencia Para más información sobre la paradoja de los gemelos y las técnicas descritas aquí, puedes consultar el libro Flat and Curved Space-Times, de G. F. R. Ellis y mío (publicado por Oxford University Press en 1988). También puede consultar los libros del Sr. Tompkins, que introducen los conceptos de la relatividad especial de forma amena y accesible.

Puede encontrar reseñas de los libros del Sr. Tompkins y pedirlos en el sitio web de Cambridge University Press; por ejemplo, consulte The New World of Mr Tompkins : George Gamow’s Classic Mr.