Ontdek de oorsprong van deling en vermenigvuldiging
In het bericht van vandaag zullen we de oorsprong uitleggen van de wiskundige symbolen van deling en vermenigvuldiging.
Het symbool van deling:
Er zijn vele manieren geweest om deling aan te duiden en we gaan de oorsprong uitleggen van enkele van de symbolen die het meest gebruikt worden en het meest bekend zijn bij iedereen.
De horizontale balk van breuken, geïntroduceerd door de Arabieren, werd voor het eerst gebruikt in Europa door de wiskundige Fibonacci in de dertiende eeuw, hoewel het gebruik ervan zich pas verspreidde in de zestiende eeuw.
De schuine balk, een variant van de horizontale, werd geïntroduceerd door De Morgan in 1845. Het was een typografisch hulpmiddel in gedrukte boeken, om de breuk in één regel te kunnen schrijven. Het symbool dat tegenwoordig veel gebruikt wordt om deling uit te drukken:
Een ander teken was het haakje, hoewel het tegenwoordig niet veel meer gebruikt wordt. Om 21 gedeeld door 3 uit te drukken, zouden we 21) 3 schrijven, en het resultaat van de deling rechts plaatsen na nog een haakje: 21) 3 (7. 
Dit teken vinden we in het werk Arithmetica integra (1544) van de Duitse wiskundige Michael Stiefel.
Dezelfde wiskundige gebruikte in zijn werk Deutsche Arithmetica (1545) ook de hoofdletters M en D om vermenigvuldiging en deling aan te duiden. Andere auteurs gebruikten ook een D, ook als omgekeerde D, zoals de Fransen, J. E. Gallimard (1685-1771), en anderen een omgekeerde d, zoals de Portugees, J. A. da Cuhna (1744-1787).
Een van de nog steeds gebruikte delingssymbolen is een balk met een punt erboven en eronder. Het werd geïntroduceerd door de Zwitserse wiskundige Johann Heinrich Rahn, in zijn werk Teutsche Algebra (1659). Dit deelteken is zeer grafisch, in die zin dat de balk van de breuk een algemene norm is.
Dit symbool was niet erg succesvol in zijn vaderland Zwitserland of in Europa. Het was dat echter wel in zowel Groot-Brittannië als de Verenigde Staten. Het is met name nog steeds het symbool dat op rekenmachines wordt gebruikt voor deling.
De Duitse wiskundige, Gottfried W. Leibniz, introduceerde de twee punten ( : ), en dit is tegenwoordig het meest gebruikte symbool. Volgens Leibniz is een van de voordelen van het gebruik van dit symbool dat de deling langs dezelfde lijn kan worden gehandhaafd en dat de relatie van deling met vermenigvuldiging, waarvoor Leibniz een punt gebruikte, behouden blijft.
Over de gnomon of hoek die we gebruiken om de factoren van de deling (deling, deler en quotiënt) van elkaar te scheiden, is niet veel informatie te vinden.
Maar Boyer, in zijn History of Mathematics, p.282, zegt: “De Arabieren, en via hen later de Europeanen, hebben de meeste van hun rekenkundige kunstgrepen van de Hindoes overgenomen, en dus is het zeer waarschijnlijk dat de methode van de ‘lange deling’ die bekend staat als de ‘galei-methode’ door de gelijkenis met een schip met de zeilen opengeklapt, ook uit India komt.” Blijkbaar gebruikte de “galei-methode” een hoek die lijkt op de hoek die nu wordt gebruikt.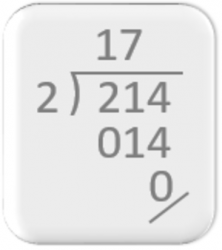
Het symbool van vermenigvuldiging:
In de tijd van de Babyloniërs gebruikten zij een ideogram: “a-du.” In het Bakhshiili manuscript, het oudste manuscript van de Indiase wiskunde, zetten zij één factor naast elkaar en verder niets. De Indiase wiskundige Bhaskara Acharia (1114-1185) gebruikte het woord “bhavita” of “bha” vlak na de factoren.
Andere wiskundigen hebben de letter M gebruikt voor vermenigvuldiging en de letter D voor deling, zoals we al eerder hebben gezegd.
In de oude tijd van de rekenkunde werd in veel algoritmen gebruik gemaakt van het kruis van San Andres om producten van deling en vermenigvuldiging en verhoudingen op te lossen. Het is wellicht om die reden dat Oughtred in 1631 dit kruis koos als symbool voor de vermenigvuldiging.
Het ondervond grote acceptatie, behalve bij de wiskundigen Gottfried W. Leibniz en Isaac Newton, die zich niet helemaal op hun gemak voelden met het symbool. Leibniz schrijft in 1698 in een van zijn brieven aan de wiskundige Johann Bernoulli: “Ik houd niet van het teken × als symbool voor vermenigvuldiging, omdat het verward kan worden met x; … Ik breng vaak eenvoudig twee grootheden in verband met een punt en geef de vermenigvuldiging aan met RS – PQ.”
Om die reden voerde Leibniz de punt in als symbool voor vermenigvuldiging.
Er zijn andere symbolen voor vermenigvuldiging geweest. Zo gebruikte de Zwitserse wiskundige Johann Rahn, (1622-1676), in zijn werk Teutsche Algebra (1659) het sterretje *. Evenals Leibniz, die eerder een omgevallen C, met de open kant naar beneden, gebruikte in zijn Dissertatio of combinatorial art (1666).
Ik hoop dat dit bericht over deling en vermenigvuldiging en de symbolen die we gebruiken om ze uit te drukken interessant is geweest.
Als je meer wilt blijven leren over deling en vermenigvuldiging, meld je dan aan voor Smartick en probeer het gratis.
Leer meer:
- Wiskunde symbolen: Groter Dan, Kleiner Dan, and Equal
- Greater Than and Less Than symbols
- Wiskundige symbolen om bewerkingen en verbanden weer te geven
- Leren hoe Romeinse cijfers te gebruiken
- Hoe op te lossen Gecombineerde Bewerkingen
- Auteur
- Recente berichten
Een multidisciplinair en multicultureel team bestaande uit wiskundigen, leraren, professoren en andere onderwijsprofessionals!
Zij streven ernaar de best mogelijke wiskundige inhoud te creëren.
- Voorbeelden van 3e graad wiskunde woordproblemen met oplossingen – 03/25/2021
- Opeenvolgende binnenhoeken: Wat ze zijn en hoe ze te vinden met voorbeelden – 03/11/2021
- Voorbeelden van woordproblemen voor de tweede graad met oplossingen – 02/04/2021