A mai bejegyzésben az osztás és a szorzás matematikai szimbólumainak eredetét ismertetjük.

Az osztás szimbóluma:

Az osztás jelölésének sokféle módja volt már, és most elmagyarázzuk a leggyakrabban használt és mindenki által legismertebb szimbólumok eredetét.
A törtek vízszintes sávját, amelyet az arabok vezettek be, Európában először a matematikus Fibonacci használta a tizenharmadik században, bár használata csak a tizenhatodik században terjedt el.

A ferde sávot, a vízszintes egy változatát De Morgan vezette be 1845-ben. Ez egy tipográfiai segédeszköz volt a nyomtatott könyvekben, hogy a törtet egyetlen sorban lehessen írni. Az osztás kifejezésére ma is széles körben használt szimbólum:
A másik jel a zárójel volt, bár jelenleg nem nagyon használják. Ha 21-et osztanánk 3-mal, akkor azt írnánk, hogy 21) 3, és az osztás eredményét egy újabb zárójel után jobbra tennénk: 21) 3 (7.

Ez a jel megtalálható Michael Stiefel német matematikus Arithmetica integra (1544) című művében.
Ez a matematikus a Deutsche Arithmetica (1545) című művében szintén a nagybetűs M és D betűket használta a szorzás és osztás jelölésére. Más szerzők is használtak D-t, beleértve a fordított D-t is, mint például a francia J. E. Gallimard (1685-1771), mások pedig bukott d-t, mint például a portugál J. A. da Cuhna (1744-1787).
Az osztás egyik ma is használatos szimbóluma egy sáv, amely felett és alatt egy pont van. Ezt a svájci matematikus, Johann Heinrich Rahn vezette be a Teutsche Algebra (1659) című művében. Ez az osztójel nagyon szemléletes, olyannyira, hogy a törtet jelző sáv egy általános norma.

Ez a szimbólum nem volt túl sikeres sem hazájában, Svájcban, sem Európában. Nagy-Britanniában és az Egyesült Államokban azonban igen. Különösen a mai napig ezt a szimbólumot használják a számológépeken az osztásra.

A német matematikus, Gottfried W. Leibniz vezette be a két pontot ( : ), és napjainkban ez a legelterjedtebb szimbólum. Leibniz szerint e szimbólum használatának egyik előnye, hogy az osztás egy vonal mentén tartható, és fenntartja az osztásnak a szorzással való kapcsolatát, amelyre Leibniz egy pontot használt.
A gnomonról vagy szögről, amelyet az osztás tényezőinek (osztó, osztó és hányados) elválasztására használunk, nem sok információ áll rendelkezésre.

De Boyer a History of Mathematics 282. oldalán azt írja: “Az arabok, és rajtuk keresztül később az európaiak, a legtöbb számtani mesterségüket a hinduktól vették át, és így nagyon valószínű, hogy a “hosszú osztás” módszere, amelyet “gályamódszer” néven ismerünk, mivel hasonlít egy hajóra, amelynek vitorlái ki vannak bontva, szintén Indiából származik”. Úgy tűnik, a “gályamódszer” a jelenleg használatoshoz hasonló szöget használt.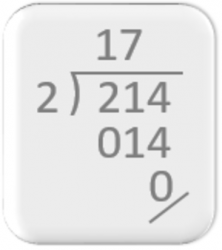

A szorzás szimbóluma:

A babilóniaiak idejében ideogramot használtak: “a-du”. A Bakhshiili kéziratban, az indiai matematika legrégebbi kéziratában egy tényezőt tettek egymás mellé, és semmi mást. Az indiai matematikus, Bhaskara Acharia (1114-1185) a “bhavita” vagy “bha” szót használta közvetlenül a tényezők után.
Más matematikusok a szorzásnál az M betűt, az osztásnál pedig a D betűt használták, ahogy azt már korábban említettük.
A számtan régi korszakában sok algoritmus használta a San Andres-i keresztet az osztás és szorzás szorzatainak és arányainak megoldására. Talán ezért is lehet, hogy 1631-ben Oughtred, ezt a keresztet választotta a szorzás szimbólumául.

Nagy elfogadottságot tapasztalt, kivéve Gottfried W. Leibniz és Isaac Newton matematikusoknál, akik nem érezték teljesen jól magukat a szimbólummal. Leibniz 1698-ban Johann Bernoulli matematikusnak írt egyik levelében ezt írja: “Nem szeretem az × jelet mint a szorzás szimbólumát, mivel összetéveszthető az x-szel; … Én gyakran két mennyiséget egyszerűen egy ponttal kapcsolok össze, és a szorzást RS – PQ-val jelzem.”

Ezért Leibniz bevezette a pontot mint a szorzás szimbólumát.
A szorzásnak voltak más szimbólumai is. Johann Rahn svájci matematikus (1622-1676) például a Teutsche Algebra (1659) című művében a * csillagot használta. Valamint Leibniz, aki korábban a Dissertatio of combinatorial art (1666) című művében (1666) egy bukott C betűt használt, nyitott oldalával lefelé.
Remélem, érdekes volt ez a bejegyzés az osztásról és szorzásról, valamint az ezek kifejezésére használt szimbólumokról.
Ha tovább szeretnél tanulni az osztásról és szorzásról, regisztrálj a Smartickre, és próbáld ki ingyenesen.

Tudj meg többet:

• Matematikai szimbólumok: Nagyobb, mint, kisebb, mint, és egyenlő
• Nagyobb, mint és kisebb, mint szimbólumok
• Matematikai szimbólumok műveletek és összefüggések ábrázolására
• Tanuld meg, hogyan használd a római számjegyeket
• How to Solve Kombinált műveletek

• Author
• Újabb bejegyzések

Tartalomkészítő csapat.
Matematikusokból, tanárokból, professzorokból és más oktatási szakemberekből álló multidiszciplináris és multikulturális csapat!
A lehető legjobb matematikai tartalmak létrehozására törekszenek.

Legújabb bejegyzések: Smartick (az összeset lásd)

• Példák 3. osztályos matematikai szöveges feladatokra megoldásokkal – 03/25/2021
• Folytonos belső szögek: Mik ezek és hogyan találjuk meg őket példákkal – 03/11/2021
• Példák második osztályos szófeladatokra megoldásokkal – 02/04/2021