V dnešním příspěvku si vysvětlíme původ matematických symbolů dělení a násobení.

Symbol dělení:

Způsobů označování dělení bylo mnoho a my si vysvětlíme původ některých nejpoužívanějších a všem nejznámějších symbolů.
Vodorovný pruh zlomků, zavedený Araby, poprvé v Evropě použil matematik Fibonacci ve třináctém století, ačkoli jeho používání se rozšířilo až ve století šestnáctém.

Šikmý pruh, variantu vodorovného, zavedl De Morgan v roce 1845. Jednalo se o typografický prostředek v tištěných knihách, aby bylo možné zapsat zlomek na jeden řádek. Symbol, který se dnes hojně používá k vyjádření dělení:
Dalším ze znaků byla závorka, i když v současnosti se příliš nepoužívá. Pokud bychom chtěli vyjádřit dělení 21 třemi, napsali bychom 21) 3 a výsledek dělení bychom umístili vpravo za další závorku: 21) 3 (7.

Toto znaménko najdeme ve spise Arithmetica integra (1544) německého matematika Michaela Stiefela.
Tentýž matematik používal velká písmena M a D k označení násobení a dělení také ve svém díle Deutsche Arithmetica (1545). Také další autoři používali písmeno D, včetně použití jako obrácené D, například Francouz J. E. Gallimard (1685-1771), a jiní spadlé d, například Portugalec J. A. da Cuhna (1744-1787).
Jedním z dosud používaných symbolů dělení je čárka s tečkou nahoře a dole. Zavedl ho švýcarský matematik Johann Heinrich Rahn ve svém díle Teutsche Algebra (1659). Tento symbol dělení je velmi názorný, a to až do té míry, že sloupec zlomku je obecnou normou.

Tento symbol neměl ve svém rodném Švýcarsku ani v Evropě velký úspěch. Ve Velké Británii i ve Spojených státech však ano. Zejména na kalkulačkách se dodnes používá jako symbol pro dělení.

Dvě tečky ( : ) zavedl německý matematik Gottfried W. Leibniz a v současnosti je to nejpoužívanější symbol. Podle Leibnize je jednou z výhod používání tohoto symbolu to, že dělení lze udržovat podél stejné přímky a zachovává se vztah dělení s násobením, pro které Leibniz používal bod.
O gnómonu neboli úhlu, který používáme k oddělení činitelů dělení (dividendy, dělitele a kvocientu), není mnoho informací.

Ale Boyer ve svých Dějinách matematiky, str. 282, říká: „Arabové a jejich prostřednictvím později Evropané převzali většinu svých aritmetických vynálezů od Hindů, a tak je velmi pravděpodobné, že metoda ‚dlouhého dělení‘, známá jako ‚galejní metoda‘ podle své podobnosti s lodí s rozvinutými plachtami, pochází také z Indie.“ „Galejní metoda“ zřejmě používala úhel podobný tomu, který se používá v současnosti.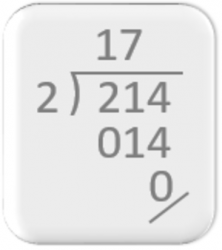

Symbol násobení:

V době Babyloňanů používali ideogram: „a-du“. V Bakšilském rukopise, nejstarším rukopise indické matematiky, kladli vedle sebe jeden činitel a nic jiného. Indický matematik Bhaskara Acharia (1114-1185) používal slovo „bhavita“ nebo „bha“ hned za faktory.
Jiní matematici používali pro násobení písmeno M a pro dělení písmeno D, jak jsme si již řekli.
V dávných dobách aritmetiky využívalo mnoho algoritmů k řešení dělení a násobení součinů a podílů kříž ze San Andres. Možná právě proto si Oughtred v roce 1631 vybral tento kříž jako symbol pro násobení.

Zaznamenal velké přijetí, s výjimkou matematiků Gottfrieda W. Leibnize a Isaaca Newtona, kterým tento symbol zcela nevyhovoval. Leibniz v roce 1698 v jednom ze svých dopisů matematikovi Johannu Bernoullimu píše: „Nemám rád symbol × jako symbol pro násobení, protože může být zaměněn za x; … často prostě spojuji dvě veličiny bodem a násobení označuji RS – PQ.“

Proto Leibniz zavedl tečku jako symbol násobení.
Existovaly i další symboly pro násobení. Například švýcarský matematik Johann Rahn, (1622-1676), použil ve svém díle Teutsche Algebra (1659) hvězdičku *. Stejně jako Leibniz, který předtím ve svém díle Dissertatio o kombinatorice (1666) použil spadlé C, otevřenou stranou dolů.
Doufám, že tento příspěvek o dělení a násobení a symbolech, které k jejich vyjádření používáme, byl zajímavý.
Pokud se chcete o dělení a násobení dozvědět více, zaregistrujte se na Smartick a vyzkoušejte si ho zdarma.

Dozvíte se více:

• Matematické symboly: Větší než, menší než, a rovná se
• Symboly větší než a menší než
• Matematické symboly pro znázornění operací a vztahů
• Naučte se, jak používat římské číslice
• Jak řešit Kombinované operace

• Autor
• Nejnovější příspěvky

Tým pro tvorbu obsahu.
Multidisciplinární a multikulturní tým složený z matematiků, učitelů, profesorů a dalších odborníků v oblasti vzdělávání!
Snaží se vytvářet ten nejlepší možný matematický obsah.

Nejnovější příspěvky od Smartick (zobrazit všechny)

• Příklady slovních úloh z matematiky pro 3. třídu s řešením – 25. 3. 2021
• Pořadové vnitřní úhly: Co to jsou a jak je najít s příklady – 03/11/2021
• Příklady slovních úloh pro 2. stupeň ZŠ s řešením – 02/04/2021