În postarea de astăzi, vom explica originea simbolurilor matematice ale împărțirii și înmulțirii.

Simbolul împărțirii:

Au existat multe moduri de a desemna diviziunea și vom explica originea unora dintre simbolurile cele mai folosite și mai cunoscute de toți.
Bara orizontală a fracțiilor, introdusă de arabi, a fost folosită pentru prima dată în Europa de către matematicianul Fibonacci în secolul al XIII-lea, deși utilizarea ei nu s-a răspândit până în secolul al XVI-lea.

Bara oblică, o variantă a celei orizontale, a fost introdusă de De Morgan în 1845. Era o resursă tipografică în cărțile tipărite, pentru a putea scrie fracția pe un singur rând. Simbolul care este utilizat pe scară largă în prezent pentru a exprima diviziunea:
Un alt semn a fost paranteza, deși în prezent nu este foarte utilizat. Pentru a exprima 21 împărțit la 3, am scrie 21) 3 și am plasa rezultatul împărțirii la dreapta, după o altă paranteză: 21) 3 (7.

Acest semn se regăsește în lucrarea Arithmetica integra (1544) a matematicianului german Michael Stiefel.
Același matematician a mai folosit literele majuscule M și D pentru a desemna înmulțirea și împărțirea în lucrarea sa Deutsche Arithmetica (1545). Alți autori au folosit, de asemenea, un D, inclusiv utilizarea ca D inversat, cum ar fi francezul J. E. Gallimard (1685-1771), iar alții un d căzut, cum ar fi portughezul J. A. da Cuhna (1744-1787).
Unul dintre simbolurile de împărțire încă în uz este o bară cu un punct deasupra și dedesubt. Acesta a fost introdus de matematicianul elvețian, Johann Heinrich Rahn, în lucrarea sa Teutsche Algebra (1659). Acest semn de împărțire este foarte grafic, până la punctul în care bara fracției este o normă generală.

Acest simbol nu a avut prea mult succes în țara sa de origine, Elveția, sau în Europa. Cu toate acestea, a avut succes atât în Marea Britanie, cât și în Statele Unite. În special, este încă simbolul folosit pe calculatoare pentru împărțire.

Matematicianul german, Gottfried W. Leibniz, a introdus cele două puncte ( : ), iar acesta este simbolul cel mai utilizat în zilele noastre. Potrivit lui Leibniz, unul dintre avantajele folosirii acestui simbol este că împărțirea se poate menține pe aceeași linie și păstrează relația împărțirii cu înmulțirea, pentru care Leibniz folosea un punct.
În ceea ce privește gnomon-ul sau unghiul pe care îl folosim pentru a separa factorii împărțirii (dividendul, divizorul și cutientul), nu există prea multe informații.

Dar Boyer, în lucrarea sa „History of Mathematics”, p.282, spune: „Arabii și, prin ei, mai târziu europenii, au adoptat majoritatea artificiilor lor aritmetice de la hinduși, așa că este foarte probabil ca metoda „diviziunii lungi”, cunoscută sub numele de „metoda galeriei”, prin asemănarea sa cu o navă cu pânzele desfășurate, să provină tot din India.” Se pare că „metoda galeriei” folosea un unghi asemănător cu cel folosit în prezent.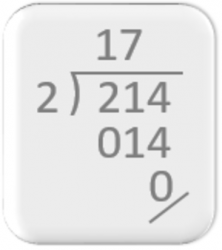

Simbolul înmulțirii:

În vremea babilonienilor, aceștia foloseau o ideogramă: „a-du”. În manuscrisul Bakhshiili, cel mai vechi manuscris de matematică indiană, ei au pus un factor unul lângă altul și nimic altceva. Matematicianul indian Bhaskara Acharia (1114-1185) a folosit cuvântul „bhavita” sau „bha” imediat după factori.
Alți matematicieni au folosit litera M pentru înmulțire și litera D pentru împărțire, așa cum am mai spus anterior.
În vechile vremuri ale aritmeticii, mulți algoritmi se foloseau de crucea lui San Andres pentru a rezolva produse de împărțire și înmulțire și proporții. Poate că din acest motiv, în 1631, Oughtred, a ales această cruce ca simbol pentru înmulțire.

A cunoscut o mare acceptare, cu excepția matematicienilor Gottfried W. Leibniz și Isaac Newton, care nu s-au simțit pe deplin confortabil cu acest simbol. Leibniz, în 1698, într-una din scrisorile sale către matematicianul Johann Bernoulli, scria: „Nu-mi place simbolul × ca simbol al înmulțirii, deoarece poate fi confundat cu x; … Adesea relaționez pur și simplu două cantități cu un punct și indic înmulțirea cu RS – PQ.”

Din acest motiv, Leibniz a introdus punctul ca simbol al înmulțirii.
Au existat și alte simboluri pentru înmulțire. De exemplu, matematicianul elvețian Johann Rahn, (1622-1676), a folosit asteriscul * în lucrarea sa Teutsche Algebra (1659). La fel ca și Leibniz, care anterior a folosit un C căzut, cu partea deschisă în jos, în lucrarea sa Dissertatio of combinatorial art (1666).
Sper că această postare despre împărțire și înmulțire și despre simbolurile pe care le folosim pentru a le exprima a fost interesantă.
Dacă doriți să continuați să învățați mai multe despre împărțire și înmulțire, înscrieți-vă la Smartick și încercați-l gratuit.

Învățați mai multe:

• Simboluri matematice: Mai mare decât, mai mic decât, and Equal
• Simboluri mai mari și mai mici decât
• Simboluri matematice pentru a reprezenta operații și relații
• Învățați cum să folosiți cifrele romane
• Cum să rezolvați Operații combinate

• Autor
• Postări recente

Echipa de creare a conținutului.
O echipă multidisciplinară și multiculturală formată din matematicieni, învățători, profesori și alți profesioniști din domeniul educației!
Se străduiesc să creeze cel mai bun conținut de matematică posibil.

Ultimele postări ale lui Smartick (vezi toate)

• Exemple de probleme de matematică de clasa a III-a cu soluții – 03/25/2021
• Unghiuri interioare consecutive: Ce sunt și cum se găsesc cu exemple – 03/11/2021
• Exemple de probleme de matematică de clasa a II-a cu soluții – 02/04/2021