Regresja logistyczna, znana również jako binarna regresja logitowa i binarna regresja logistyczna, jest szczególnie użyteczną techniką modelowania predykcyjnego. Jest używana do przewidywania wyników obejmujących dwie opcje, na przykład, czy głosowałeś lub nie głosowałeś. Poniżej postaram się po prostu wyjaśnić, co oznaczają wagi, gdy używasz ich do interpretacji.

Interpretacja wag w regresji logistycznej różni się od interpretacji wag w regresji liniowej, ponieważ wynik w regresji logistycznej jest prawdopodobieństwem między 0 a 1. Wagi nie wpływają już liniowo na prawdopodobieństwo. Suma ważona jest przekształcana przez funkcję logistyczną w prawdopodobieństwo. Dlatego musimy przeformułować równanie interpretacyjne tak, aby po prawej stronie wzoru znajdował się tylko człon liniowy.

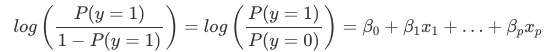
Ten człon w funkcji log() nazywamy odds (prawdopodobieństwo zdarzenia podzielone przez prawdopodobieństwo braku zdarzenia), a zawinięty w logarytm nazywamy log odds.

Z tego wzoru wynika, że model regresji logistycznej jest modelem liniowym dla log odds. Świetnie! To nie brzmi pomocnie! Przy niewielkim przetasowaniu pojęć można dowiedzieć się, jak zmienia się prognoza, gdy jedna z cech xjxj zostanie zmieniona o 1 jednostkę. Aby to zrobić, możemy najpierw zastosować funkcję exp() do obu stron równania:

Następnie porównujemy, co się stanie, gdy zwiększymy jedną z wartości cechy o 1. Ale zamiast patrzeć na różnicę, patrzymy na stosunek dwóch predykcji:

Stosujemy następującą regułę:

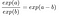
I usuwamy wiele terminów:

W końcu mamy coś tak prostego jak exp() wagi cechy. Zmiana cechy o jedną jednostkę zmienia iloraz szans (multiplikatywny) o współczynnik exp(βj)exp(βj). Możemy to również zinterpretować w ten sposób: Zmiana w xjxj o jedną jednostkę zwiększa log odds ratio o wartość odpowiadającej jej wagi. Większość ludzi interpretuje iloraz szans, ponieważ wiadomo, że myślenie o log() czegoś jest trudne dla mózgu. Interpretacja ilorazu szans wymaga już pewnego przyzwyczajenia. Na przykład, jeśli masz szanse 2, oznacza to, że prawdopodobieństwo dla y=1 jest dwa razy większe niż y=0. Jeśli masz wagę (= logarytm współczynnika szans) 0.7, wtedy zwiększenie odpowiedniej cechy o jedną jednostkę mnoży szanse o exp(0.7) (w przybliżeniu 2) i szanse zmieniają się na 4. Ale zazwyczaj nie zajmujesz się szansami i interpretujesz wagi tylko jako współczynniki szans. Ponieważ aby faktycznie obliczyć szanse, musiałbyś ustawić wartość dla każdej cechy, co ma sens tylko wtedy, gdy chcesz spojrzeć na jeden konkretny przypadek zestawu danych.

Oto interpretacje dla modelu regresji logistycznej z różnymi typami cech:

• Cecha liczbowa: Jeśli zwiększymy wartość cechy xjxj o jedną jednostkę, to szacowane szanse zmieniają się o współczynnik exp(βj)exp(βj)
• Cecha kategoryczna binarna: Jedną z dwóch wartości cechy jest kategoria referencyjna (w niektórych językach ta zakodowana w 0). Zmiana cechy xjxj z kategorii referencyjnej na drugą kategorię zmienia szacowane szanse o współczynnik exp(βj)exp(βj).
• Cecha kategoryczna z więcej niż dwiema kategoriami: Jednym z rozwiązań radzenia sobie z wieloma kategoriami jest one-hot-encoding, co oznacza, że każda kategoria ma swoją własną kolumnę. Potrzebujesz tylko L-1 kolumn dla cechy kategorycznej z L kategoriami, w przeciwnym razie jest ona nadmiernie sparametryzowana. L-ta kategoria jest wtedy kategorią odniesienia. Możesz użyć dowolnego innego kodowania, które może być używane w regresji liniowej. Interpretacja dla każdej kategorii jest wtedy równoważna interpretacji cech binarnych.
• Intercept β0β0: Gdy wszystkie cechy liczbowe są równe zero, a cechy kategoryczne są w kategorii odniesienia, szacowane szanse są exp(β0)exp(β0). Interpretacja wagi punktu przecięcia nie jest zazwyczaj istotna.

.