Jak zdefiniowano w tej pracy, graf kołowy rzędu , czasami nazywany po prostu kołem (Harary 1994, s. 46; Pemmaraju i Skiena 2003, s. 248; Tutte 2005, s. 78), jest grafem, który zawiera cykl rzędu i dla którego każdy wierzchołek grafu w cyklu jest połączony z jednym innym wierzchołkiem grafu zwanym piastą. Krawędzie koła, które obejmują piastę, nazywamy szprychami (Skiena 1990, s. 146). Koło może być zdefiniowane jako graf połączony , gdzie jest grafem singletonowym, a jest grafem cyklu, co czyni go grafem stożkowym.

Zauważ, że istnieją dwie konwencje indeksowania dla grafów kołowych, przy czym niektórzy autorzy (np., Gallian 2007), przyjmują konwencję, że oznacza graf kołowy na węzłach.

Graf tetraedryczny (tj. ) jest izomorficzny do , a jest izomorficzny do kompletnego grafu trójdzielnego . W ogólności, graf kołowy jest szkieletem piramidy.

jest jednym z dwóch grafów otrzymanych przez usunięcie dwóch krawędzi z grafu pentatopowego , drugim jest graf domu X.

Grafy kołowe są wdzięczne (Frucht 1979).

Graf kołowy ma wymiar grafu 2 dla (a więc jest jednostkowy) i wymiar 3 w pozostałych przypadkach (a więc nie jest jednostkowy) (Erdős et al. 1965, Buckley i Harary 1988).

Dowolny graf kołowy jest grafem samodualnym.

Grafy kołowe można skonstruować w języku Wolfram Language za pomocą WheelGraph. Wstępnie obliczone własności pewnej liczby grafów kołowych są dostępne za pomocą GraphData.

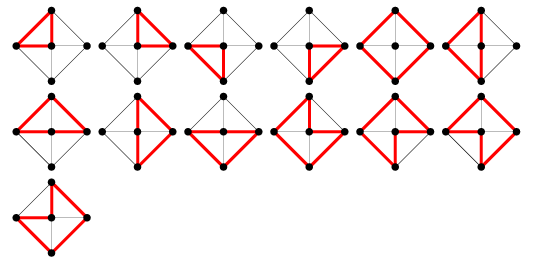
Liczba cykli grafu w grafie kołowym jest dana przez , lub 7, 13, 21, 31, 43, 57, … (OEIS A002061) dla , 5, ….

W grafie kołowym piasta ma stopień , a pozostałe węzły mają stopień 3. Grafy kołowe są 3-połączone. , gdzie jest grafem zupełnym czwartego rzędu. Liczba chromatyczna grafu wynosi

(1)

Graf kołowy ma stopień . graf kołowy ma wielomian chromatyczny

(2)

.