GeeksforGeeks
Metoda Sumy Ważonej jest wielokryterialną metodą podejmowania decyzji, w której będzie wiele alternatyw i musimy określić najlepszą alternatywę w oparciu o wiele kryteriów. Istnieją inne dostępne metody, w tym Metoda Produktu Ważonego (WPM), Technika Porządkowania Preferencji przez Podobieństwo do Idealnego Rozwiązania (TOPSIS), VIKOR, MOORA, GTMA itp. Zrozummy, że Metoda Sumy Ważonej działa na przykładzie.
Rozważmy przypadek, w którym musimy wybrać najlepszego kandydata spośród 5 kandydatów, którzy pojawiają się na rozmowę kwalifikacyjną. Tabela 1 składa się z danych 5 studentów, które obejmują ich CGPA, wynagrodzenie, które oczekują na miesiąc, ich wyniki w egzaminie technicznym i ocen osiągniętych przez nich w teście umiejętności.
Tabela 1: Przykładowy zestaw danych
| Atrybut | CGPA | Oczekiwana pensja | Wynik egzaminu technicznego | Test umiejętności. Grade |
|---|---|---|---|---|
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8,5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Rozważmy następujące wagi przyjęte przez panel przeprowadzający rozmowy kwalifikacyjne :
CGPA = 30%, Expected Stipend = 20%, Technical Exam Score = 25%, Aptitute Test Grade = 25%
Tabela 2: Wagi poszczególnych atrybutów
| Attribute | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8,5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Atrybut korzystny to taki, w którym osoba pragnie maksymalnych wartości. Tutaj CGPA, wynik egzaminu technicznego i wyniki testu umiejętności są korzystnymi atrybutami, ponieważ firma oczekuje, że studenci będą mieli więcej z tych atrybutów.
Niekorzystny atrybut to taki, w którym pożądane są minimalne wartości. W tym przypadku oczekiwane stypendium jest nie-korzystnym atrybutem. Firma zatrudnia osoby, które są skłonne pracować więcej z niskim wynagrodzeniem.
Teraz zobaczmy, który student zostanie wybrany przez firmę za pomocą metody sumy ważonej.
W tym celu musimy znormalizować wartości w tabeli 2.
- Dla atrybutów korzystnych,
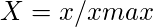
- Dla atrybutów niekorzystnych,
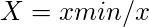
Tabela 3: Decydowanie o maksymalnej wartości dla atrybutu korzystnego i minimalnej wartości dla atrybutu nie korzystnego
| Atrybut | CGPA | Oczekiwane stypendium | Punktacja z egzaminu technicznego | Ocena z testu umiejętności |
|---|---|---|---|---|
| Waga | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | B1 |
| Student 2 | 7.6 | 8500(min) | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2(max) |
| Student 5 | 9.3(max) | 14000 | 72 | A2 |
W systemie ocen uwzględnimy następujące punkty
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabela 4: Aktualizacja ocen z testu umiejętności
| Atrybut | CGPA | Przewidywane stypendium | Punktacja z egzaminu technicznego | Ocena z testu umiejętności |
|---|---|---|---|---|
| Waga | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | 3 |
| Student 2 | 7.6 | 8500(min) | 68 | 3 |
| Student 3 | 8,2 | 9500 | 63 | 2 |
| Student 4 | 8.5 | 10000 | 70 | 4(max) |
| Student 5 | 9.3(max) | 14000 | 72 | 4 |
Normalizuj wartości dla danego atrybutu w zależności od atrybutu korzystnego i niekorzystnego.
Tabela 5: Normalizacja
| Atrybut | CGPA | Przewidywane stypendium | Wynik egzaminu technicznego | Ocena z testu umiejętności |
|---|---|---|---|---|
| Waga | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Student 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Student 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Student 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Student 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabela 6: The Weight- Normalized decision matrix
| Attribute | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0,9677 | 0,7083 | 1 | 0.75 |
| Student 2 | 0,8172 | 1 | 0,9444 | 0,75 |
| Student 3 | 0,8817 | 0,8947 | 0.875 | 0,5 |
| Student 4 | 0,9134 | 0,85 | 0,9722 | 1 |
| Student 5 | 1 | 0.6071 | 1 | 1 |
Tabela 7: Mnożenie każdego parametru z odpowiednimi wagami
| Atrybut | CGPA | Przewidywane stypendium | Punktacja z egzaminu technicznego | Ocena z testu umiejętności |
|---|---|---|---|---|
| Waga | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0,9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Student 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Student 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Student 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0.25 |
| Student 5 | 1 × 0.3 | 0.6071 × 0.2 | 1 × 0.25 | 1 × 0.25 |
Powyższa tabela jest uproszczona w następujący sposób
Tabela 8: Uproszczona wersja tabeli 7
| Atrybut | CGPA | Przewidywane stypendium | Punktacja z egzaminu technicznego | Ocena z testu umiejętności |
|---|---|---|---|---|
| Waga | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0.29031 | 0,14166 | 0,25 | 0,1875 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0,25 |
| Student 5 | 0,3 | 0,12142 | 0,25 | 0.25 |
Musimy dodać składniki w każdym wierszu i obliczyć sumę ważoną, która jest wynikiem wydajności i nadać priorytety uczniom
Tabela 9: Obliczanie rangi uczniów według wyników
| Atrybut | CGPA | Oczekiwane stypendium | Technical Exam Score | Aptitude Test Grade | Performance Score | Rank |
|---|---|---|---|---|---|---|
| Weight | 0.3 | 0,2 | 0,25 | 0,25 | ||
| Student 1 | 0,29031 | 0,14166 | 0,25 | 0,1875 | 0.86947 | 3 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 | 0.86876 | 4 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Student 5 | 0,3 | 0,12142 | 0.25 | 0,25 | 0,92142 | 2 |
Wnioski : Z metody sumy ważonej wynika, że uczeń 4 jest najlepszym wyborem spośród innych.