9.4: Why Can’t We See Molecules?
Najprostszym sposobem określenia struktury cząsteczek byłoby „zobaczyć”, jak rozmieszczone są jądra i jak rozmieszczone są elektrony. Nie jest to możliwe przy użyciu światła widzialnego, ponieważ długość fali światła widzialnego jest znacznie większa niż zwykłe wymiary cząsteczek. Wiązka elektronów może mieć wymagane krótkie fale, ale małe cząsteczki organiczne są szybko niszczone przez napromieniowanie elektronami o odpowiedniej długości fali. Niemniej jednak, mikroskopia elektronowa jest cenną techniką do badania dużych cząsteczek, takich jak DNA, które mogą być barwione atomami metali ciężkich przed oglądaniem, lub same są dość stabilne dla wiązki elektronów (Rysunki 9-4 i 9-5).

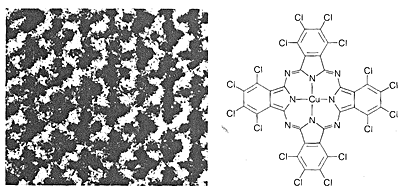
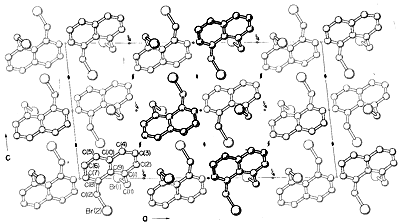
Praktycznie wszystkie części widma promieniowania elektromagnetycznego, od promieni X do fal radiowych, mają pewne praktyczne zastosowanie w badaniach cząsteczek organicznych. Szczególną wartość ma wykorzystanie dyfrakcji rentgenowskiej do określania struktury cząsteczek w kryształach, a w ciągu ostatnich dziesięciu lat technika ta stała się niemal rutynowa. Rysunek 9-6 przedstawia szczegółowy układ węgli, hydrogenów i bromów w 1,8-bis(bromometylo)naftalenie (1), określony metodą dyfrakcji rentgenowskiej. Stosowana aparatura i techniki są bardzo złożone i nie są jeszcze dostępne dla bardzo wielu laboratoriów organicznych.
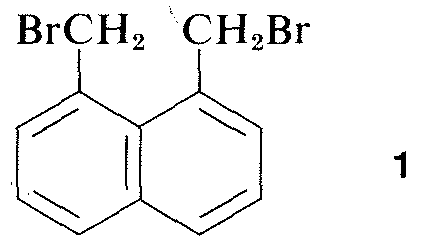
Inne metody dyfrakcyjne obejmują dyfrakcję elektronów, która może być stosowana do „określania struktur gazów lub lotnych substancji ciekłych, które nie mogą być otrzymane jako kryształy odpowiednie do dyfrakcji rentgenowskiej, oraz dyfrakcję neutronów, która ma specjalne zastosowanie do kryształów, w których pożądana jest dokładna lokalizacja hydrogenów. Wodór nie ma wystarczającej siły rozpraszania promieniowania rentgenowskiego, aby być precyzyjnie zlokalizowany przez dyfrakcję rentgenowską.
Metody dyfrakcyjne mogą być stosowane do określania kompletnych struktur cząsteczek organicznych, ale nie są one wystarczająco rutynowe, aby mogły być powszechnie wykorzystywane w praktycznej pracy w laboratorium organicznym. Z tego powodu, w pozostałej części tego rozdziału położymy nacisk na te formy spektroskopii, które są ogólnie dostępne dla rutynowych zastosowań laboratoryjnych. Jak się okaże, metody te są wykorzystywane przez chemików organicznych w mniej lub bardziej empiryczny sposób. Ogólnie rzecz biorąc, metody spektroskopowe zależą od jakiejś formy wzbudzenia cząsteczek przez absorpcję promieniowania elektromagnetycznego i, jak już powiedzieliśmy, praktycznie wszystkie części widma elektromagnetycznego są użyteczne w tym zakresie. Powszechnie stosowany zakres widma elektromagnetycznego jest pokazany na rysunku 9-7 wraz z porównaniem różnych jednostek, które są stosowane do wyrażenia energii lub długości fali.
Główne rodzaje spektroskopii stosowane do analizy strukturalnej związków organicznych są wymienione w tabeli 9-1. Pokazano zakres częstotliwości absorbowanego promieniowania, jak również efekt wytwarzany przez promieniowanie i specyficzny rodzaj informacji, który jest wykorzystywany w analizie strukturalnej. Po krótkim przedstawieniu zasad spektroskopii, opiszemy metody, które są najbardziej przydatne w praktycznej pracy laboratoryjnej. Niemniej jednak, bardzo ważne jest, aby być świadomym innych, mniej rutynowych metod, które mogą być wykorzystywane do rozwiązywania specjalnych problemów, a niektóre z nich są omówione w tym rozdziale oraz w rozdziałach 19 i 27.
Możesz mieć problemy z relacjami między różnymi jednostkami długości fali i częstotliwości powszechnie stosowanych w spektroskopii. Związek pomiędzy długością fali, częstotliwością i prędkością powinien stać się dla Ciebie jasny, jeśli zastanowisz się nad tym, że stoisz na molo i obserwujesz fale oceanu. Zakładając, że fale są równomiernie rozłożone, odległość pomiędzy grzbietami fal będzie jednakowa, co odpowiada długości fali. Grzbiety fal będą mijały się z określoną liczbą na minutę, co oznacza częstotliwość. Prędkość, z jaką fale przemieszczają się obok ciebie, jest związana z prędkościami ∗ i ∗ przez zależność c = ∗ ∗. To, co jest prawie niepotrzebnie skomplikowane, to różnorodność jednostek powszechnie używanych do wyrażania ∗ (∗lambda) i ∗ (∗nu) dla promieniowania elektromagnetycznego. Jednym z problemów jest tradycja, drugim chęć uniknięcia bardzo dużych lub bardzo małych liczb. Tak więc, jak pokazuje Rysunek 9-7, możemy być zainteresowani długościami fal elektromagnetycznych, które różnią się nawet o współczynnik ∗(10^{16}}). Ponieważ prędkość promieniowania elektromagnetycznego w próżni jest stała i wynosi 3 razy 10^8 \), częstotliwości będą się różnić o ten sam współczynnik.
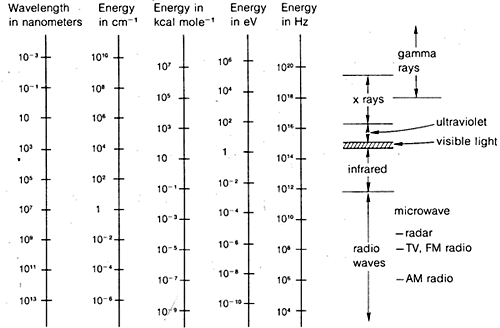
Jednostki częstotliwości są wyrażane w cyklach na sekundę (cps) lub hercach (ertz), które są równoważne (radiany na sekundę są szeroko stosowane przez fizyków).
Table 9-1: Principal Spectroscopic Techniques Currently in Use for Analysis of Molecular Structure

(^3)Użyteczny opis tego, jak struktury molekularne mogą być określone przez „rentgenowskie widzenie” jest podany w rozdziale XI Organic Molecules in Action autorstwa M. Goodman i F. Morehouse, Gordon and Breach, New York, 1973.
- John D. Robert i Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, wydanie drugie. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. Ta treść jest chroniona prawem autorskim na następujących warunkach: „Udzielono zezwolenia na indywidualne, edukacyjne, badawcze i niekomercyjne powielanie, rozpowszechnianie, wyświetlanie i wykonywanie tej pracy w dowolnym formacie.”
.