Come definito in questo lavoro, un grafo ruota di ordine , talvolta chiamato semplicemente ruota (Harary 1994, p. 46; Pemmaraju e Skiena 2003, p. 248; Tutte 2005, p. 78), è un grafo che contiene un ciclo di ordine e per il quale ogni vertice del grafo nel ciclo è connesso a un altro vertice del grafo detto mozzo. I bordi di una ruota che includono il mozzo sono chiamati raggi (Skiena 1990, p. 146). La ruota può essere definita come l’unione del grafo , dove è il grafo singoletto e è il grafo del ciclo, rendendolo un grafo -conico.

Si noti che esistono due convenzioni per l’indicizzazione dei grafi a ruota, con alcuni autori (ad esempio, Gallian 2007), adottano la convenzione che denota il grafo a ruota su nodi.

Il grafo tetraedrico (cioè ) è isomorfo a , e è isomorfo al grafo tripartito completo . In generale, il grafo -ruota è lo scheletro di una piramide .

è uno dei due grafi ottenuti rimuovendo due bordi dal grafo pentatopo , l’altro è il grafo casa X.

I grafi ruota sono graziosi (Frucht 1979).

Il grafo a ruota ha dimensione 2 per (e quindi è a distanza unitaria) e dimensione 3 altrimenti (e quindi non a distanza unitaria) (Erdős et al. 1965, Buckley e Harary 1988).

Ogni grafo a ruota è un grafo auto-duale.

I grafi a ruota possono essere costruiti nel linguaggio Wolfram usando WheelGraph. Le proprietà precalcolate di un certo numero di grafi a ruota sono disponibili tramite GraphData.

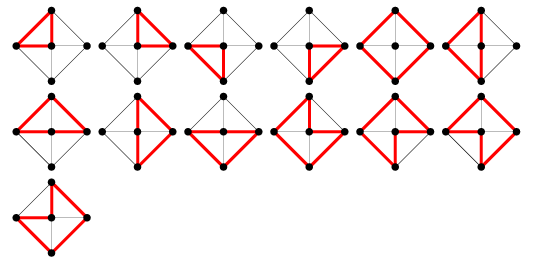
Il numero di cicli del grafico a ruota è dato da , o 7, 13, 21, 31, 43, 57, … (OEIS A002061) per , 5, ….

In un grafo a ruota, il mozzo ha grado , e gli altri nodi hanno grado 3. I grafi a ruota sono 3 connessi. , dove è il grafo completo di ordine quattro. Il numero cromatico di è

(1)

Il grafico della ruota ha polinomio cromatico

(2)