GeeksforGeeks
Il Metodo della Somma Ponderata è un metodo decisionale multi-criterio in cui ci saranno più alternative e dobbiamo determinare la migliore alternativa basata su più criteri. Ci sono altri metodi disponibili tra cui Weighted Product Method (WPM), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, MOORA, GTMA ecc. Capiamo come funziona il Metodo della Somma Ponderata con un esempio.
Consideriamo un caso in cui dobbiamo selezionare il miglior candidato tra 5 candidati che si presentano a un colloquio. La tabella 1 consiste nei dettagli dei 5 studenti che includono il loro CGPA, lo stipendio che si aspettano al mese, i loro punteggi nell’esame tecnico e i voti da loro ottenuti nel test attitudinale.
Tabella 1: Set di dati campione
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Test attitudinale Grado |
|---|---|---|---|---|
| Studente 1 | 9 | 12000 | 72 | B1 |
| Studente 2 | 7.6 | 8500 | 68 | B1 |
| Studente 3 | 8.2 | 9500 | 63 | B2 |
| Studente 4 | 8.5 | 10000 | 70 | A2 |
| Studente 5 | 9.3 | 14000 | 72 | A2 |
Considera i pesi assunti dalla commissione d’intervista come segue:
CGPA = 30%, Stipendio previsto = 20%, Punteggio esame tecnico = 25%, Voto test attitudinale = 25%
Tabella 2: I pesi di ogni attributo
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 9 | 12000 | 72 | B1 |
| Studente 2 | 7.6 | 8500 | 68 | B1 |
| Studente 3 | 8.2 | 9500 | 63 | B2 |
| Studente 4 | 8.5 | 10000 | 70 | A2 |
| Studente 5 | 9.3 | 14000 | 72 | A2 |
L’attributo vantaggioso è quello in cui la persona desidera i valori massimi. Qui, il CGPA, il punteggio dell’esame tecnico e i punteggi dei test attitudinali sono attributi vantaggiosi perché la società si aspetta che gli studenti abbiano più di questi attributi.
L’attributo non vantaggioso è quello in cui si desiderano valori minimi. In questo caso lo stipendio previsto è un attributo non benefico. L’azienda assume persone che sono disposte a lavorare di più con uno stipendio basso.
Ora vediamo quale studente deve essere selezionato dall’azienda usando il metodo della somma pesata.
Per questo, dobbiamo normalizzare i valori nella tabella 2.
- Per gli attributi benefici,
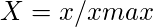
- Per gli attributi non benefici,
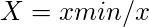
Tabella 3: Decidere il valore massimo per un attributo vantaggioso e il valore minimo per un attributo non vantaggioso
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 9 | 12000 | 72(max) | B1 |
| Studente 2 | 7.6 | 8500(min) | 68 | B1 |
| Studente 3 | 8.2 | 9500 | 63 | B2 |
| Studente 4 | 8.5 | 10000 | 70 | A2(max) |
| Studente 5 | 9.3(max) | 14000 | 72 | A2 |
Prendiamo in considerazione i seguenti punti per il sistema dei voti
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabella 4: Aggiornamento dei voti della prova attitudinale
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado prova attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 9 | 12000 | 72(max) | 3 |
| Studente 2 | 7.6 | 8500(min) | 68 | 3 |
| Studente 3 | 8.2 | 9500 | 63 | 2 |
| Studente 4 | 8.5 | 10000 | 70 | 4(max) |
| Studente 5 | 9.3(max) | 14000 | 72 | 4 |
Normalizzare i valori per il rispettivo attributo a seconda dell’attributo benefico e non benefico.
Tabella 5: Normalizzazione
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Studente 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Studente 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Studente 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Studente 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabella 6: La matrice di decisione normalizzata dal peso
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 0.9677 | 0.7083 | 1 | 0.75 |
| Studente 2 | 0.8172 | 1 | 0.9444 | 0.75 |
| Studente 3 | 0.8817 | 0.8947 | 0.875 | 0.5 |
| Studente 4 | 0.9134 | 0.85 | 0.9722 | 1 |
| Studente 5 | 1 | 0.6071 | 1 | 1 |
Tabella 7: Moltiplicando ogni parametro con i rispettivi pesi
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 0.9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Studente 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Studente 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Studente 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0,25 |
| Studente 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
La tabella precedente è semplificata come segue
Tabella 8: Versione semplificata della tabella 7
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale |
|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 |
| Studente 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 |
| Studente 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Studente 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Studente 4 | 0.27402 | 0.17 | 0.24305 | 0.25 |
| Studente 5 | 0.3 | 0.12142 | 0.25 | 0.25 |
Dobbiamo sommare i componenti di ogni riga e calcolare la somma ponderata che è il punteggio di rendimento e dare le priorità agli studenti
Tabella 9: Calcolo del rango degli studenti in base al punteggio di rendimento
| Attributo | CGPA | Stipendio previsto | Punteggio esame tecnico | Grado test attitudinale | Punteggio performance | Classifica |
|---|---|---|---|---|---|---|
| Peso | 0.3 | 0.2 | 0.25 | 0.25 | ||
| Studente 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 | 0.86947 | 3 |
| Studente 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 | 0.86876 | 4 |
| Studente 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Studente 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Studente 5 | 0,3 | 0,12142 | 0.25 | 0.25 | 0.92142 | 2 |
Conclusione : Dal metodo della somma pesata, si decide che lo studente 4 è la scelta migliore tra gli altri.