La regressione logistica, conosciuta anche come logit binario e regressione logistica binaria, è una tecnica di modellazione predittiva particolarmente utile. Viene utilizzata per prevedere i risultati che coinvolgono due opzioni, se hai votato o non hai votato per esempio. Di seguito cercherò di spiegare solo cosa significano i pesi quando li usate per le interpretazioni.

L’interpretazione dei pesi nella regressione logistica differisce dall’interpretazione dei pesi nella regressione lineare, poiché il risultato nella regressione logistica è una probabilità tra 0 e 1. I pesi non influenzano più linearmente la probabilità. La somma ponderata viene trasformata dalla funzione logistica in una probabilità. Quindi dobbiamo riformulare l’equazione per l’interpretazione in modo che solo il termine lineare sia sul lato destro della formula.

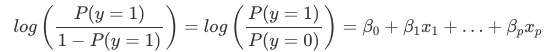
Chiamiamo il termine nella funzione log() “odds” (probabilità di evento diviso per probabilità di nessun evento) e avvolto nel logaritmo si chiama log odds.

Questa formula mostra che il modello di regressione logistica è un modello lineare per il log odds. Grande! Non sembra utile! Con un piccolo rimescolamento dei termini, si può capire come cambia la previsione quando una delle caratteristiche xjxj viene cambiata di 1 unità. Per fare questo, possiamo prima applicare la funzione exp() a entrambi i lati dell’equazione:

Poi confrontiamo cosa succede quando aumentiamo di 1 unità uno dei valori delle caratteristiche. Ma invece di guardare la differenza, guardiamo il rapporto delle due previsioni:

Applichiamo la seguente regola:

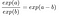
E rimuoviamo molti termini:

Alla fine, abbiamo qualcosa di semplice come exp() del peso di una caratteristica. Un cambiamento di una caratteristica di una unità cambia l’odds ratio (moltiplicativo) di un fattore di exp(βj)exp(βj). Potremmo anche interpretarlo in questo modo: Un cambiamento in xjxj di un’unità aumenta il log odds ratio del valore del peso corrispondente. La maggior parte delle persone interpreta l’odds ratio perché è noto che pensare al log() di qualcosa è difficile per il cervello. Interpretare l’odds ratio richiede già un po’ di abitudine. Per esempio, se avete probabilità di 2, significa che la probabilità per y=1 è doppia rispetto a y=0. Se avete un peso (= log odds ratio) di 0.7, allora aumentando la rispettiva caratteristica di una unità moltiplica le probabilità per exp(0.7) (circa 2) e le probabilità cambiano a 4. Ma di solito non vi occupate delle probabilità e interpretate i pesi solo come odds ratio. Perché per calcolare effettivamente le probabilità avreste bisogno di impostare un valore per ogni caratteristica, il che ha senso solo se volete guardare un’istanza specifica del vostro set di dati.

Queste sono le interpretazioni per il modello di regressione logistica con diversi tipi di caratteristiche:

• Funzione numerica: Se si aumenta il valore della caratteristica xjxj di una unità, le probabilità stimate cambiano di un fattore di exp(βj)exp(βj)
• Funzione categorica binaria: Uno dei due valori della caratteristica è la categoria di riferimento (in alcune lingue, quella codificata in 0). Cambiare la caratteristica xjxj dalla categoria di riferimento all’altra categoria cambia le probabilità stimate di un fattore di exp(βj)exp(βj).
• Funzione categoriale con più di due categorie: Una soluzione per trattare con più categorie è la codifica one-hot, cioè ogni categoria ha la propria colonna. Avete bisogno solo di L-1 colonne per una caratteristica categoriale con L categorie, altrimenti è sovra-parametrizzata. La L-esima categoria è quindi la categoria di riferimento. Potete usare qualsiasi altra codifica che può essere usata nella regressione lineare. L’interpretazione per ogni categoria allora è equivalente all’interpretazione delle caratteristiche binarie.
• Intercetta β0β0: Quando tutte le caratteristiche numeriche sono zero e le caratteristiche categoriche sono alla categoria di riferimento, le probabilità stimate sono exp(β0)exp(β0). L’interpretazione del peso dell’intercetta di solito non è rilevante.