Hur man tolkar vikterna i logistisk regression
Logistisk regression, även känd som binär logit och binär logistisk regression, är en särskilt användbar teknik för prediktiv modellering. Den används för att förutsäga utfall som omfattar två alternativ, till exempel om du röstade eller inte röstade. Nedan ska jag försöka att bara förklara vad vikterna betyder när man använder dem för tolkningar.
Tolkningen av vikterna i logistisk regression skiljer sig från tolkningen av vikterna i linjär regression, eftersom utfallet i logistisk regression är en sannolikhet mellan 0 och 1. Vikterna påverkar inte längre sannolikheten linjärt. Den viktade summan omvandlas av den logistiska funktionen till en sannolikhet. Därför måste vi omformulera ekvationen för tolkningen så att endast den linjära termen finns på höger sida av formeln.
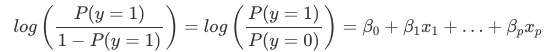
Vi kallar termen i log()-funktionen för ”odds” (sannolikhet för händelse dividerad med sannolikhet för ingen händelse) och inlindad i logaritmen kallas den för log odds.
Denna formel visar att den logistiska regressionsmodellen är en linjär modell för log odds. Bra! Det låter inte särskilt hjälpsamt! Med lite omblandning av termerna kan du räkna ut hur förutsägelsen förändras när en av egenskaperna xjxj ändras med 1 enhet. För att göra detta kan vi först tillämpa funktionen exp() på båda sidor av ekvationen:

Därefter jämför vi vad som händer när vi ökar ett av funktionsvärdena med 1. Men istället för att titta på skillnaden tittar vi på förhållandet mellan de två förutsägelserna:

Vi tillämpar följande regel:
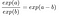
Och vi tar bort många termer:

I slutändan har vi något som är lika enkelt som exp() för en funktionsvikt. En förändring av en funktion med en enhet förändrar oddskvoten (multiplikativt) med en faktor exp(βj)exp(βj). Vi skulle också kunna tolka det på detta sätt: En förändring av xjxj med en enhet ökar log oddskvoten med värdet av motsvarande vikt. De flesta människor tolkar oddskvoten eftersom det är känt att det är svårt för hjärnan att tänka på log() av något. Att tolka oddskvoten kräver redan en viss tillvänjning. Om man till exempel har oddset 2 betyder det att sannolikheten för y=1 är dubbelt så stor som för y=0. Om man har en vikt (= log oddskvot) på 0,7 betyder det att om man ökar respektive funktion med en enhet multipliceras oddset med exp(0,7) (ungefär 2) och att oddset ändras till 4. Men vanligen behandlar man inte oddset utan tolkar bara vikterna som oddskvoter. För för att faktiskt beräkna oddsen skulle du behöva ange ett värde för varje funktion, vilket bara är meningsfullt om du vill titta på en specifik instans av ditt dataset.
Det här är tolkningarna för den logistiska regressionsmodellen med olika funktionstyper:
- Numerisk funktion: Om du ökar värdet av funktionen xjxj med en enhet ändras de uppskattade oddsen med en faktor exp(βj)exp(βj)
- Binär kategorisk funktion: Ett av de två värdena för funktionen är referenskategorin (på vissa språk den som kodas med 0). Om man ändrar funktionen xjxj från referenskategorin till den andra kategorin ändras det uppskattade oddset med en faktor exp(βj)exp(βj).
- Kategorisk funktion med mer än två kategorier: En lösning för att hantera flera kategorier är one-hot-kodning, vilket innebär att varje kategori har en egen kolumn. Man behöver bara L-1 kolumner för en kategorisk funktion med L kategorier, annars blir den överparameteriserad. Den L:e kategorin är då referenskategorin. Du kan använda vilken annan kodning som helst som kan användas i linjär regression. Tolkningen för varje kategori är då likvärdig med tolkningen av binära egenskaper.
- Intercept β0β0: När alla numeriska egenskaper är noll och de kategoriska egenskaperna befinner sig på referenskategorin är de skattade oddsen exp(β0)exp(β0). Tolkningen av interceptvikten är vanligtvis inte relevant.