Az e műben meghatározottak szerint, egy rendű kerékgráf, amelyet néha egyszerűen -keréknek neveznek (Harary 1994, p. 46; Pemmaraju és Skiena 2003, 248. o.; Tutte 2005, 78. o.), olyan gráf, amely tartalmaz egy rendű ciklust, és amelynek minden egyes gráfcsúcsa a ciklusban egy másik gráfcsúccsal, az úgynevezett csomóponttal van kapcsolatban. A keréknek azokat az éleit, amelyek a hubot tartalmazzák, küllőknek nevezzük (Skiena 1990, 146. o.). A kerék úgy definiálható, mint a gráf egyesítése, ahol a szingleton gráf és a ciklusgráf, így ez egy -kúpos gráf.

Megjegyezzük, hogy a kerékgráfok indexelésére kétféle konvenció létezik, egyes szerzők (pl, Gallian 2007) azt a konvenciót fogadják el, hogy a csomópontokon lévő kerékgráfot jelöli.

A tetraéderes gráf (azaz ) izomorf a -vel, a pedig izomorf a teljes hármas gráffal. Általában a -kerékgráf egy -piramis váza.

egyike annak a két gráfnak, amelyet a pentatop gráfból két él eltávolításával kapunk, a másik a ház X gráfja.

A kerékgráfok kecsesek (Frucht 1979).

A kerékgráf esetén 2-es gráfdimenziójú (tehát egységtávolságú), egyébként 3-as dimenziójú (tehát nem egységtávolságú) (Erdős et al. 1965, Buckley és Harary 1988).

Minden kerékgráf önduális gráf.

A kerékgráfok a Wolfram Nyelvben a WheelGraph segítségével konstruálhatók. Számos kerékgráf előre kiszámított tulajdonságai elérhetők a GraphData segítségével.

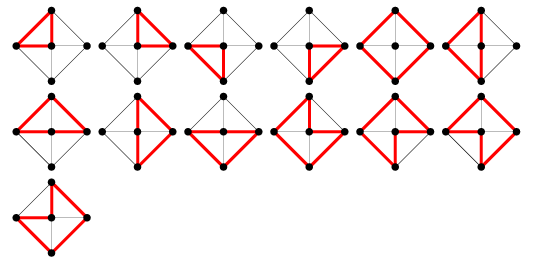
A kerékgráfban a gráfciklusok száma , vagy 7, 13, 21, 21, 31, 43, 57, … (OEIS A002061) a , 5, ….

A kerékgráfban a csomópont fokú, a többi csomópont pedig 3 fokú. A kerékgráfok 3-as összeköttetésűek. , ahol a négyes rendű teljes gráf. A kromatikus száma

(1)

a kerékgráf kromatikus polinomja

(2)