A logisztikus regresszió, más néven bináris logit és bináris logisztikus regresszió, különösen hasznos előrejelző modellezési technika. Két lehetőséget magában foglaló kimenetel előrejelzésére használják, például arra, hogy szavazott-e vagy nem szavazott. Az alábbiakban megpróbálom csak elmagyarázni, hogy mit jelentenek a súlyok, amikor az értelmezésekhez használja őket.

A logisztikus regresszióban a súlyok értelmezése eltér a lineáris regresszióban használt súlyok értelmezésétől, mivel a logisztikus regresszióban a kimenet egy 0 és 1 közötti valószínűség. A súlyok már nem lineárisan befolyásolják a valószínűséget. A súlyozott összeget a logisztikus függvény valószínűséggé alakítja át. Ezért az értelmezéshez szükséges egyenletet úgy kell újrafogalmaznunk, hogy a képlet jobb oldalán csak a lineáris kifejezés szerepeljen.

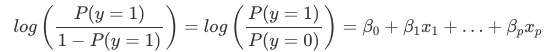
A log()-függvényben szereplő kifejezést esélynek (az esemény valószínűsége osztva az esemény nélküli valószínűséggel) nevezzük, és logaritmusba csomagolva log esélynek nevezzük.

Ez a képlet azt mutatja, hogy a logisztikus regressziós modell a log esély lineáris modellje. Nagyszerű! Ez nem hangzik hasznosnak! A kifejezések egy kis átrendezésével kideríthetjük, hogyan változik az előrejelzés, ha az xjxj egyik jellemzőt 1 egységgel megváltoztatjuk. Ehhez először az exp() függvényt alkalmazhatjuk az egyenlet mindkét oldalára:

Ezt követően összehasonlítjuk, mi történik, ha az egyik jellemző értékét 1-gyel növeljük. De a különbség helyett a két előrejelzés arányát nézzük:

A következő szabályt alkalmazzuk:

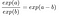
És sok kifejezést eltávolítunk:

A végén valami olyan egyszerűt kapunk, mint egy jellemző súly exp(). Egy jellemző egy egységnyi változása exp(βj)exp(βj) tényezővel változtatja meg az esélyhányadot (multiplikatív). Ezt így is értelmezhetjük: Az xjxj egy egységnyi változása a megfelelő súly értékével növeli a log esélyhányadost. A legtöbb ember azért értelmezi az esélyhányadost, mert valaminek a log() értékéről való gondolkodás köztudottan megviseli az agyat. Az esélyhányados értelmezése már némi megszokást igényel. Ha például az odds értéke 2, az azt jelenti, hogy y=1 valószínűsége kétszer akkora, mint y=0. Ha a súly (= log odds ratio) 0,7, akkor a megfelelő tulajdonság egy egységgel való növelése exp(0,7)-el (kb. 2) megszorozza az oddsot, és az odds 4-re változik. De általában nem foglalkozunk az oddsokkal, és a súlyokat csak az odds-arányokként értelmezzük. Ugyanis az esélyek tényleges kiszámításához minden egyes jellemzőhöz értéket kellene megadni, aminek csak akkor van értelme, ha az adatállományunk egy adott példányát szeretnénk vizsgálni.

Ezek a logisztikus regressziós modell értelmezései különböző jellemzőtípusokkal:

• Numerikus jellemző: Ha az xjxj jellemző értékét egy egységgel növeli, a becsült esélyek exp(βj)exp(βj)
• Bináris kategorikus jellemző: A jellemző két értéke közül az egyik a referenciakategória (egyes nyelveken a 0-val kódolt). Az xjxj jellemzőnek a referencia-kategóriáról a másik kategóriára történő megváltoztatása exp(βj)exp(βj) tényezővel változtatja a becsült esélyt.
• Kettőnél több kategóriát tartalmazó kategorikus jellemző: Az egyik megoldás a több kategória kezelésére a one-hot-kódolás, ami azt jelenti, hogy minden kategóriának saját oszlopa van. Egy L kategóriával rendelkező kategorikus jellemzőhöz csak L-1 oszlopra van szükség, különben túlparaméterezett lesz. Az L-edik kategória ekkor a referencia-kategória. Bármilyen más, lineáris regresszióban használható kódolást használhat. Az egyes kategóriák értelmezése ekkor egyenértékű a bináris jellemzők értelmezésével.
• Intercept β0β0: Ha minden numerikus jellemző nulla, és a kategorikus jellemzők a referencia-kategóriánál vannak, akkor a becsült esélyek exp(β0)exp(β0). Az intercept súlyának értelmezése általában nem releváns.