GeeksforGeeks
A súlyozott összeg módszer egy többkritériumos döntéshozatali módszer, amelyben több alternatíva lesz, és több kritérium alapján kell meghatározni a legjobb alternatívát. Vannak más módszerek is, többek között a súlyozott termék módszer (WPM), a TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), VIKOR, MOORA, GTMA stb. Értsük meg a súlyozott összeg módszer működését egy példán keresztül.
Tegyük fel egy olyan esetet, amikor egy interjúra jelentkező 5 jelölt közül kell kiválasztanunk a legjobbat. Az 1. táblázat az 5 diák adatait tartalmazza, amely tartalmazza a CGPA-jukat, a havonta elvárt fizetésüket, a műszaki vizsgán elért eredményeiket és az alkalmassági vizsgán elért jegyeiket.
1. táblázat:
Tekintsük az interjúztató testület által feltételezett súlyokat a következőképpen :
CGPA = 30%, Várható ösztöndíj = 20%, Szakvizsga eredmény = 25%, Aptitute teszt jegye = 25%
2. táblázat: Az egyes attribútumok súlyai
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsga pontszáma | Értékelési teszt fokozat |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 9 | 12000 | 72 | B1 |
| Tanuló 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
A jótékony tulajdonság az, amelyben az ember maximális értékekre vágyik. Itt a CGPA, a műszaki vizsga pontszáma és az alkalmassági teszt pontszámai előnyös attribútumok, mivel a vállalat elvárja, hogy a diákok több ilyen attribútummal rendelkezzenek.
A nem előnyös attribútum olyan attribútum, amelyben minimális értékeket kívánnak. Ebben az esetben a várható ösztöndíj egy nem előnyös attribútum. A vállalat az alacsony ösztöndíjjal többet dolgozni hajlandó embereket túráztatja.
Most nézzük meg, hogy melyik diákot választja ki a vállalat a súlyozott összeg módszerrel.
Ezért a 2. táblázatban szereplő értékeket normalizálnunk kell.
- A hasznos tulajdonságok esetében
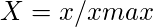
- A nem hasznos tulajdonságok esetében
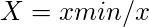
3. táblázat: A hasznos attribútum maximális értékének és a nem hasznos attribútum minimális értékének meghatározása
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsgaeredmény | Aptitude Test Grade |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 9 | 12000 | 72(max) | B1 |
| Tanuló 2 | 7.6 | 8500(min) | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2(max) |
| Student 5 | 9.3(max) | 14000 | 72 | A2 |
Az osztályzatrendszerhez a következő pontokat vesszük figyelembe
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
4. táblázat: Az alkalmassági vizsga jegyeinek frissítése
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsga pontszáma | Egyetemi jegy |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 9 | 12000 | 72(max) | 3 |
| Tanuló 2 | 7.6 | 8500(min) | 68 | 3 |
| Tanuló 3 | 8.2 | 9500 | 63 | 2 |
| Tanuló 4 | 8.5 | 10000 | 70 | 4(max) |
| Student 5 | 9.3(max) | 14000 | 72 | 4 |
Normáljuk az adott attribútum értékeit a hasznos és nem hasznos attribútumtól függően.
5. táblázat: Normalizálás
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsgaeredmény | Aptitude Test Grade |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Tanuló 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Tanuló 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Student 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Student 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
6. táblázat: A súlyokkal normalizált döntési mátrix
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsgaeredmény | Aptitude Test Grade |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 0.9677 | 0.7083 | 1 | 0.75 |
| Tanuló 2 | 0.8172 | 1 | 0.9444 | 0.75 |
| Tanuló 3 | 0.8817 | 0.8947 | 0.875 | 0.5 |
| Student 4 | 0.9134 | 0.85 | 0.9722 | 1 |
| Student 5 | 1 | 0.6071 | 1 | 1 |
7. táblázat: Az egyes paraméterek szorzása a megfelelő súlyokkal
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsga eredménye | Aptitude Test Grade |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 0.9677 × 0.3 | 0.7083 × 0.2 | 1 × 0.25 | 0.75 × 0.25 |
| Student 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Tanuló 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Tanuló 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0.25 |
| Tanuló 5 | 1 × 0.3 | 0.6071 × 0.2 | 1 × 0.25 | 1 × 0.25 |
A fenti táblázat a következőképpen egyszerűsödik
8. táblázat: A 7. táblázat egyszerűsített változata
| Attribútum | CGPA | Várható ösztöndíj | Technikai vizsga eredménye | Aptitude Test Grade |
|---|---|---|---|---|
| Súly | 0.3 | 0.2 | 0.25 | 0.25 |
| Tanuló 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Tanuló 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 |
| Student 5 | 0.3 | 0.12142 | 0.25 | 0.25 |
Az egyes sorok összetevőit össze kell adnunk, és ki kell számolnunk a súlyozott összeget, ami a teljesítménypontszám, és meg kell adnunk a prioritásokat a tanulóknak
9. táblázat: A hallgatók rangsorának kiszámítása a teljesítménypontszámok alapján
| Attribútum | CGPA | Várható ösztöndíj | Technical Exam Score | Aptitude Test Grade | Performance Score | Rank |
|---|---|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 | ||
| Tanuló 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 | 0.86947 | 3 |
| Tanuló 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 | 0.86876 | 4 |
| Tanuló 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Tanuló 5 | 0.3 | 0.12142 | 0.25 | 0.25 | 0.92142 | 2 |
Következtetés : A súlyozott összeg módszer alapján az a döntés született, hogy a 4. tanuló a legjobb választás a többiek közül.