Introduction

A közelmúltban javasoltuk az asszociatív információ-visszakeresés olyan mechanizmusát, amely explicit módon figyelembe veszi a memóriaelemek hosszú távú neuronális reprezentációit (Romani et al., 2013). A modell egyik alapvető jóslata a “könnyű” és “nehéz” szavak létezése. Ezt a jóslatot igazoltuk a Michael Kahana laboratóriumában gyűjtött szabad felidézési kísérletek nagy adathalmazának elemzése során, ahol kimutattuk, hogy a felidézendő szavak valószínűsége konzisztens az alanyok tetszőlegesen kiválasztott csoportjai között (Katkov et al., submitted). Az e megfigyelések által felvetett természetes kérdés az, hogy a felidézési kísérletekben a szavak nehézségét milyen jellemzőkkel lehet előre jelezni, különösen, hogy ha egyáltalán hozzájárul a szóhossz.

A szóhossz-hatás korábbi vizsgálatainak többsége olyan listákat használt, amelyek kifejezetten rövid vagy hosszú szavakból álltak össze. Két korábbi vizsgálatban, ahol váltakozva rövid és hosszú szavakból álló listákat használtak, nem figyeltek meg szóhosszhatást (Hulme et al., 2004; Jalbert et al., 2011). Jelen hozzájárulásunk szabad felidézési paradigmát használ, és sokkal nagyobb adathalmazon alapul, mint a korábbi tanulmányok. Arról számolunk be, hogy a szavak véletlenszerű kiválasztásakor, függetlenül azok hosszától, a hosszú szavak jobban felidéződnek, mint a rövidek, ami látszólag ellentmond a klasszikus szóhosszhatásnak mind a soros, mind a szabad felidézésben (Baddeley et al., 1975; Russo és Grammatopoulou, 2003; Tehan és Tolan, 2007; Bhatarah et al., 2009). Ennek az ellentmondásnak a lehetséges feloldását a (Romani et al., 2013) asszociatív előhívási modelljének keretében adjuk meg.

Anyagok és módszerek

Kísérleti módszerek

A kéziratban közölt adatokat M. Kahana laboratóriumában gyűjtötték a Penn Electrophysiology of Encoding and Retrieval Study részeként (a kísérletek részleteit lásd Miller et al., 2012). Itt annak a 141 résztvevőnek az eredményeit elemeztük (17-30 évesek), akik a kísérlet első, hét kísérleti ülésből álló szakaszát végezték el. A résztvevők a Pennsylvaniai Egyetem IRB protokollja szerint adták beleegyezésüket, és kompenzációt kaptak a részvételükért. Minden egyes ülés 16 darab 16 szavas listából állt, amelyeket egyenként mutattak be a számítógép képernyőjén, és körülbelül 1,5 órán át tartottak. Minden egyes vizsgálati listát egy azonnali szabad felidézési teszt követett. A szavakat egy 1638 szóból álló készletből választották ki. Minden egyes lista esetében 1500 ms késleltetés volt az első szó megjelenése előtt a képernyőn. Minden egyes elem 3000 ms-ig volt a képernyőn, majd 800-1200 ms inter-stimulus intervallum (egyenletes eloszlás) következett. A lista utolsó eleme után 1200-1400 ms jitterelt késleltetés következett, majd a résztvevő 75 másodpercet kapott arra, hogy megpróbálja felidézni az imént bemutatott elemek bármelyikét. Minden próbát felhasználtunk; a behatolásokat és az ismétléseket eltávolítottuk a próbákból.

A modell

Feltételezzük, hogy minden szót egy véletlenszerűen kiválasztott neuronpopuláció képvisel a dedikált memóriahálózatban. Feltételezzük továbbá, hogy minden egyes előhívott elem belső támpontként működik a következő elemhez az elemek közötti hasonlósági mértéknek megfelelően, amelyet a megfelelő populációk közötti metszéspont méreteként határozunk meg (a két elemet reprezentáló neuronok száma). A (Romani et al., 2013) nyomán olyan előhívási folyamatot veszünk figyelembe, amelyet közvetlenül az elemek memóriareprezentációi határoznak meg, a hálózati aktivitás explicit szimulálása nélkül. A visszahívás dinamikáját a visszahívott elemek szekvenciája írja le. Az elsőt véletlenszerűen választjuk ki a bemutatottak közül, és minden következő visszahívott elemet úgy választunk ki, hogy az legyen az, amelyik maximális hasonlóságot mutat az éppen visszahívott elemmel, nem számítva az éppen “meglátogatott” elemet (Romani et al., 2013). A visszahívás akkor fejeződik be, amikor a visszahívási folyamat egy ciklusba kerül, és már nem lehet több elemet visszahívni.

A kísérleti protokoll (lásd fentebb) utánzásához W = 1638 N hosszúságú véletlen bináris mintát generáltunk: {ξiw = 0; 1}, ahol w = 1, … , W; i = 1, … , N jelöli a hálózat neuronjait, úgy, hogy ξiw = 1, ha az i neuron részt vesz a w memóriaelem kódolásában. A w és w′ elemek közötti hasonlóságot ezután a következőképpen számítjuk ki: Sww′=∑i=1Nξiwξiw′. Az egyes elemekhez tartozó mintakomponenseket egymástól függetlenül sorsoltuk ki a ξiw = 1 valószínűségű pw-val, amelyet a következő módon választottunk ki: minden mintához önkényesen hozzárendeltünk egy lw = 1…4 szótaghosszúságot úgy, hogy az lw eloszlása a minták között megegyezett a kísérletben használt szavak megfelelő eloszlásával (a négynél hosszabb szótaghosszúságú szavakat öt szóval kombináltuk a négyes hosszúságúakkal). Az adott lw értékű minták esetében a megfelelő pw értékek egyenletesen oszlottak el 0,02 – 10-3lw és 0,02 + 10-3lw között. A mintastatisztikák ilyen megválasztásával az adott elemet reprezentáló neuronok átlagos száma nem függ a szótaghosszúságtól, míg a szórás a szótaghosszúsággal növekszik. A szóreprezentációk ezután a szimulált kísérlet során végig rögzítettek voltak.

Minden egyes szimulált felidézési kísérlethez L = 16 elemet választottunk ki a bemutatásra két kísérleti protokoll szerint. Az elsőnél a tételeket teljesen függetlenül választottuk ki, mint Kahana kísérletében. A második protokoll esetében az azonos lw-vel rendelkező tételeket véletlenszerűen választották ki. A visszahívási folyamatot a (Romani et al., 2013) szerint szimuláltuk. Az első felidézett elemet véletlenszerűen választottuk ki a bemutatott elemek közül. A felidézett elemek közötti későbbi átmeneteket a köztük lévő S hasonlósági mátrix határozta meg, amelynek minden egyes elemét a megfelelő reprezentációk metszéspontjában lévő neuronok számaként számoltuk ki: Sww′=∑i=1Nξiwξiw′. Pontosabban, a következő előhívott elem az, amelyik a legnagyobb hasonlósággal rendelkezik az aktuálisan előhívott elemhez, kizárva azt az elemet, amelyet közvetlenül az aktuális elem előtt hívtak elő. A visszahívás akkor fejeződik be, amikor a visszahívási folyamat egy ciklusba kerül, és már nem lehet több elemet visszahívni.

Eredmények

Elemeztünk egy nagy adathalmazt, amely 141 alany által végzett szabad visszahívási kísérleteket tartalmazott, alanyonként 112 próbával. Az adatokat Michael Kahana laboratóriumában gyűjtöttük. A listák 16 szóból álltak, amelyeket véletlenszerűen választottak ki egy 1638 szóból álló készletből. Minden próbát felhasználtunk; a behatolásokat és az ismétléseket eltávolítottuk a próbákból (összesen 15792 próba, lásd a Módszerek fejezetet). Minden szó esetében az általános felidézési valószínűséget (Prec) úgy számoltuk ki, mint a próbák hányadát idéztük fel a szó bemutatásakor. Az 1. ábra a (Prec) eloszlását mutatja az adott szótagszámú szavak (fekete) összesített eloszlását az összes próbából. A Prec eloszlása minden szóhosszúság esetén széles. Mindazonáltal a felidézés átlagos valószínűsége és szórása monoton nő a szótagok számával (a korrelációs együttható 0,15, p < 10-6).

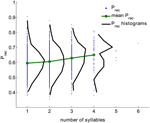
1. ábra. A különböző szótagszámú szavak felidézési valószínűsége (kék pontok), a felidézési valószínűségek eloszlása (fekete) és a felidézési valószínűség kísérleti adatokból számított átlagértéke (zöld). A szótagszám és a felidézési valószínűség közötti korrelációs együttható 0,15, p < 10-6).

Ez az eredmény látszólag ellentmond a klasszikus szóhosszhatásnak, ahol a rövid szavak listáiról kimutatták, hogy jobban felidéződnek, mint a hosszabb szavak listáiról (Baddeley et al., 1975; Russo és Grammatopoulou, 2003; Tehan és Tolan, 2007; Bhatarah et al., 2009). Annak tesztelésére, hogy mindkét hatás magyarázható-e az általunk javasolt előhívási mechanizmussal, két feltételben szimuláltuk a modellt kísérleti paradigmákat imitálva – szabad előhívás rövid/hosszú szavakból és véletlenszerű listákból összeállított listákkal (lásd Módszerek). Meglepő eredményre jutottunk: a teljesítmény a szabad visszahívás feladatban a kísérleti paradigmától függ – a nem összefüggő szavak véletlenszerű keverékéből álló listák visszahívásában a hosszabb szavak statisztikailag könnyebben felidézhetők, míg a rögzített szótagszámú szavakból összeállított listákban a rövidebb szavak könnyebben felidézhetők (2. ábra).

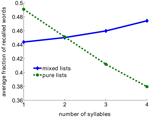
2. ábra. A felidézett szavak átlagos töredéke a modellben szereplő szótagszám függvényében. A tiszta listákat csak azonos szótagszámú szavak felhasználásával állítottuk össze. A vegyes listákat a teljes szóállományból állították össze.

A klasszikus szóhosszhatások legtöbb magyarázata azt feltételezi, hogy a bemutatott ingerek teljes hossza negatívan korrelál a felidézett szavak számával. Annak tesztelésére, hogy ezt az állítást alátámasztják-e az adatok, kiszámítottuk a bemutatott listák szótagszáma és a felidézett szavak száma közötti korrelációt. Gyakorlatilag nem találtunk korrelációt (a korrelációs együttható 0,004, és nem különbözik szignifikánsan 0-tól, p = 0,67).

Diszkusszió

A szóhosszhatást, azaz azt a megfigyelést, hogy a rövid szavakból álló listákat jobban felidézik, mint a hosszú szavakból álló listákat (Baddeley et al., 1975), a rövid távú memória elméleteinek egyik kulcsjelenségének tekintik (Campoy, 2011; Jalbert et al., 2011). Itt arról számolunk be, hogy nem kapcsolódó szavak szabad felidézése során, ahol a rövid és hosszú szavak véletlenszerűen keverednek, a hosszú szavak felidézési valószínűsége nagyobb, mint a rövideké, ami látszólag ellentmond a szóhosszhatásnak.

A klasszikus szóhosszhatást hagyományosan vagy a hosszabb tételek nagyobb komplexitásával (Neath és Nairne, 1995), vagy a hosszabb tételek hosszabb próbálási idejével magyarázzák (Baddeley, 1986, 2003; Page és Norris, 1998; Burgess és Hitch, 1999). Az első magyarázat azt sugallja, hogy a rövidebb szavakat általánosságban könnyebb felidézni, ami nem összeegyeztethető a megfigyelésünkkel. A második magyarázat szerint a rövidebb próbálási idő miatt a rövid szavakból többet lehet elpróbálni, és ezért többet idézünk fel belőlük. Ez a magyarázat nem határozza meg, hogy a bemutatott szavakat milyen sorrendben próbálnánk újra, de negatív korrelációt sugall a bemutatott elemek teljes hossza és a visszahívott szavak száma között, miközben az adatokban nincs ilyen korreláció.

Itt megmutatjuk, hogy az asszociatív előhívás nemrég javasolt mechanizmusa potenciálisan magyarázza mind a klasszikus szóhosszhatást (amely a szabad előhívási kísérletekben is jelen van, lásd Russo és Grammatopoulou, 2003; Bhatarah et al., 2009), mind a véletlenszerűen kiválasztott szavak listáiban jelentkező ellentétes hosszúsági hatást, amelyről ebben a hozzájárulásban számoltunk be. A meglévő modellekkel ellentétben a mi modellünkben a tételek hosszú távú neuronális reprezentációja döntő szerepet játszik, és nincs szükség külön rövid távú memória mechanizmusra. Különösen a véletlenszerű listákban szereplő elemek felidézési valószínűsége növekszik a reprezentációjuk méretével a többi elemhez képest, és ezeket az elemeket hamarabb felidézik, és elnyomják a kisebb reprezentációjú elemeket (Romani et al., 2013). A teljes tételsor átlagos visszahívási valószínűsége azonban független az átlagos reprezentációs mérettől, de negatívan függ a reprezentációs méret varianciájától a tételsoron belül (Katkov et al., submitted). Ezért feltételeztük, hogy a hosszabb szavak átlagosan nem rendelkeznek nagyobb reprezentációval, mint a rövidebbek, de együttesen nagyobb a reprezentáció méretének varianciája. Ennek a feltételezésnek jelenleg nincs közvetlen biológiai igazolása, de lehetővé tette számunkra a kísérleti megfigyelések közötti látszólagos ellentmondás összeegyeztetését. Különösen a klasszikus szóhossz-hatást magyarázza, amikor csak az adott szótaghosszúságú szavak kerülnek bemutatásra, és ezért a reprezentáció méretének varianciája a szótaghosszal együtt nő. A vegyes szótaghosszúságú listákban egyes próbákban a hosszabb szótaghosszúságú elemek rendelkeznek a legnagyobb neuronális reprezentációval. Az ilyen listák bemutatásakor a hosszabb szavak nagyobb valószínűséggel idéződnek fel, elnyomva a többi elem felidézését, ami enyhe pozitív korrelációt eredményez egy elem szótaghossza és felidézési valószínűsége között.

A jelen hozzájárulásban bemutatott eredmények azt mutatják, hogy a szó hossza kiemelkedő tényező, amely befolyásolja a szó felidézésének könnyűségét. Megjegyezzük azonban, hogy a felidézési valószínűségek még adott hosszúságú szavak esetében is széles eloszlást mutatnak, ami arra utal, hogy más, eddig ismeretlen szójellemzők is hozzájárulnak egy szó felidézésének valószínűségéhez.

Interdekütközésre vonatkozó nyilatkozat

A szerzők kijelentik, hogy a kutatást olyan kereskedelmi vagy pénzügyi kapcsolatok hiányában végezték, amelyek potenciális összeférhetetlenségként értelmezhetők.

Köszönet

Hálásak vagyunk M. Kahanának, amiért nagylelkűen megosztotta velünk a laboratóriumában kapott adatokat. Kahana laboratóriumát az NIH MH55687-es ösztöndíja támogatja. Misha Tsodyksot az EU FP7 (604102-es támogatási megállapodás), az Izraeli Tudományos Alapítvány és az Adelis Alapítvány támogatja. Sandro Romanit a Human Frontier Science Program hosszú távú ösztöndíja támogatja.