Hurok

A “ciklus utasítások” nem mások, mint a többlépéses folyamatok automatizálása műveletsorozatok szervezésével és az ismétlésre szoruló részek csoportosításával. Szintén a programozás központi része, az iteráció (vagy Looping) adja a számítógépek teljesítményének nagy részét. Egy lépéssorozatot annyiszor tudnak megismételni, ahányszor csak szükséges, és az egyszerű lépések megfelelő ismétlésével összetett problémákat is meg lehet oldani.

Általánosságban kétféle “Looping technikát” különböztetünk meg:

1. “For Loops”: azok, amelyek egy számláló vagy egy index által vezérelve meghatározott számú alkalommal hajtódnak végre.
2. “While Loops” és “Repeat Loops”: egy logikai feltétel bekövetkeztén és ellenőrzésén alapulnak. A feltétel vizsgálata a cikluskonstrukció kezdetén vagy végén történik.

Vessünk rájuk egy pillantást:

1) For ciklusok

Ezekben a vezérlési struktúrákban az utasítások egymás után, egymást követő sorrendben hajtódnak végre egy értéksorozaton, amely csak a “For ciklus” indításakor kerül kiértékelésre (soha nem értékelődik újra). Ebben az esetben az iterációk száma rögzített és előre ismert.

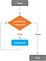
Ha egy változóra (amely egy meghatározott sorozaton belüli értékeket vehet fel) vonatkozó feltétel kiértékelése TRUE eredményt ad, akkor egy vagy több utasítás egymás után végrehajtásra kerül az adott értéksorozaton. Amint az első feltételvizsgálat megtörtént (és eredménye TRUE), az utasítás végrehajtásra kerül, és a feltétel kiértékelése ismét megtörténik, egy iteratív folyamaton keresztül. A “változó a sorozatban” rész ezt a tesztet a sorozat minden egyes értékén elvégzi, amíg az utolsó elemre nem terjed ki.

Ha a feltétel nem teljesül, és az eredmény FALSE (pl. a “változó a sorozatban” rész befejezte a sorozat összes elemének végigjárását), a ciklus véget ér. Ha a feltételvizsgálat eredménye az első iterációban FALSE, a “For Loop” soha nem kerül végrehajtásra.

A “For ciklusok” szintaxisa a következő:

Példa 1

A “For ciklusok” működésének bemutatásához először létrehozunk egy sorozatot, különböző gyümölcsnevek összekapcsolásával egy (“gyümölcs_lista” nevű) lista létrehozásához:

Ezt a gyümölcslistát fogjuk használni “szekvenciaként” egy “For Loop”-ban, és a “For Loop”-ban a szekvencia minden megadott értékére (a gyümölcslistában szereplő különböző gyümölcsök) egyszer lefuttatunk egy utasítást (minden érték nevét kiírjuk):

Így a “For Loop” eredménye a következő:

## "Apple"
## "Kiwi"
## "Orange"
## "Banana"

OK, tehát a listában szereplő minden egyes érték nevét kiírtuk. Nem nagy dolog, igaz? A jó dolog az, hogy a “For hurkok” segítségével még érdekesebb eredményeket lehet elérni. Nézzük meg a következő példát:

Példa 2

Mi van akkor, ha értékeket akarunk módosítani, vagy számításokat akarunk egymás után végrehajtani? A “For ciklusok” segítségével matematikai műveleteket végezhetünk szekvenciálisan egy vektor minden egyes értékén (azonos típusú elemek, ami ebben az esetben numerikus lesz).

Ebben a példában létrehozunk egy számsorozatot (1-től 10-ig), és beállítunk egy “For Loop”-ot, hogy kiszámítsa és kiírja a sorozat minden egyes értékének négyzetgyökét:

Ez esetben a “For Loop” eredménye a következő:

 1
 1.414214
 1.732051
 2
 2.236068
 2.449490
 2.645751
 2.828427
 3
 3.162278

Mindenféle matematikai operátort használhatunk egy számsorozat felett, és ahogy a cikk későbbi részében látni fogjuk, mindenféle kombinációkat készíthetünk a különböző vezérlési struktúrák között, hogy összetettebb eredményeket érjünk el.

2) While Loops

A “While Loops”-ban először egy feltételt értékelünk ki, és ha a feltétel tesztelésének eredménye TRUE, akkor egy vagy több utasítást ismételten végrehajtunk, amíg a feltétel FALSE nem lesz.

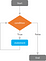
Az “If utasításokkal” ellentétben, amelyekben egy TRUE-ként tesztelt feltétel csak egyszer hajt végre egy kifejezést és véget ér, a “While Loops” iteratív utasítások, amelyek újra és újra végrehajtanak valamilyen kifejezést, amíg a feltétel FALSE nem lesz. Ha a feltétel soha nem bizonyul FALSE-nek, a “While Loop” örökké fog tartani, és a program összeomlik. Fordítva, ha a feltétel vizsgálata a ciklus elején FALSE eredményt ad, a kifejezés soha nem fog végrehajtódni.

A “While Loops” szintaxisa a következő:

Példa 1

Lássunk egy példát. Először is létrehozunk egy változót (x), és hozzáadjuk az 1 értéket. Ezután beállítunk egy “While Loop”-ot, hogy iteratívan teszteljen egy feltételt ezen a változó felett, amíg a feltétel tesztelésének eredménye FALSE:

Így működik: a változó (x) kezdeti értéke 1, így amikor teszteljük a feltételt “az (x) változó kisebb, mint 10?”.”, az eredmény TRUE-ra értékelődik, és a kifejezés végrehajtódik, kiírva az (x) változó eredményét, ami az első esetben 1. De aztán történik valami: az (x) változót a függvény vége előtt 1-gyel növeljük, és a következő iterációban az x értéke 2 lesz.

Ez a változó átcsoportosítása azért fontos, mert végül elérjük a FALSE feltételt és a ciklusból való kilépést (x értéke = 10). A kezdeti feltételek megváltoztatásának elmulasztása a “While Loop”-ban végtelen ciklushoz és a program összeomlásához vezet.

Kimenet

 1
 2
 3
 4
 5
 6
 7
 8
 9

Példa 2

Hallott már a Fibonacci-sorozatról? Ez egy olyan számsorozat, amelynek az a tulajdonsága, hogy a sorban következő számot az előtte lévő két szám összeadásával találjuk meg: 0, 1, 1, 1, 2, 3, 5, 8, 13, 21,… Ez a sorozat számos természeti jelenségben megtalálható, és különböző alkalmazásokkal rendelkezik a pénzügyekben, a zenében, az építészetben és más tudományágakban.

Kalkuláljuk ki egy “While Loop” segítségével.

Ez esetben a sorozatban egy maximális értéket állítunk be megállási feltételként, így a ciklus csak a 100 alatti számok esetén írja ki a Fibonacci-sorozatot. Amikor egy sorozatelem (bármelyik is legyen az) 100-nál nagyobb lesz, a ciklusciklus véget ér.

 0
 1
 1
 2
 3
 5
 8
 13
 21
 34
 55
 89

3. példa

A Fibonacci-sorozat “While Loop”-al történő generálásának másik módja, hogy a sorozat maximális értékének stopfeltételként való beállítása helyett megadjuk a generálni kívánt sorozatelemek számát.

Ez a “While Loop” a sorozat következő elemét az előző elem végéhez csatolja, amíg el nem éri a leállítási feltételt. Ebben az esetben, amikor a sorozat eléri a 10 elemet (függetlenül attól, hogy milyen értékeket), a ciklusciklus véget ér.

Kimenet

 0 1 1 2 3 5 8 13 21 34

3) Ismétlési ciklusok

A “While ciklusokhoz” szorosan kapcsolódó “Ismétlési ciklusok” iteratív módon hajtják végre az utasításokat, de mindaddig, amíg egy leállítási feltétel nem teljesül. Ily módon az utasítások legalább egyszer végrehajtódnak, függetlenül attól, hogy mi a feltétel eredménye, és a ciklus csak akkor lép ki, amikor bizonyos feltétel TRUE lesz:

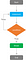
A “Repeat Loop” szintaxisa a következő:

A “Ismétlő ciklusok” megszakítási feltételként “megszakítási utasításokat” használnak. A “Break utasítások” egy feltétel tesztelésével kombinálva megszakítják a ciklusokat a ciklusokon belül, mivel amikor a program elér egy break-et, akkor a vezérlést a ciklus vége után közvetlenül következő utasításra adja át (ha van ilyen).

A “Repeat Loops” örökké fog futni, ha a break feltétel nem teljesül. Lásd ezt a 2 példát

1. példa

Először létrehozunk egy változót (x), és hozzáadjuk az 5 értéket. Ezután beállítunk egy “Ismétlődési hurkot”, hogy iteratívan kiírja a változó értékét, módosítsa a változó értékét (növelje 1-gyel), és teszteljen egy feltételt a változó felett (ha egyenlő 10), amíg a feltétel tesztjének eredménye TRUE nem lesz.

A “megszakító feltétel” akkor lép működésbe, amikor a változó (x) eléri a 10-et, és a ciklus véget ér.

Kimenet

 5
 6
 7
 8
 9

2. példa

Most tegyük fel, hogy véletlen számok listáját állítjuk elő, amelyeknek nem ismerjük a generálás sorrendjét vagy sorrendjét.

Ebben a példában egy “ismétlődési hurok” segítségével normális eloszlású véletlen számok sorozatát generáljuk (bármilyen más eloszlással is generálhatunk véletleneket, mi csak ezt választottuk), és a sorozatot megszakítjuk, amint az egyik szám nagyobb lesz 1-nél. Mivel nem tudjuk, hogy melyik számok jönnek először, nem tudjuk, hogy milyen hosszú lesz a sorozat: csak a megszakítási feltételt ismerjük.

Először is a “set.seed” utasítással rögzítjük a véletlenszámokat (mindig ugyanazokat a véletlenszámokat generáljuk), és reprodukálhatóvá tesszük ezt a példát.

Ezután elindítjuk az “Ismétlődési hurkot” egy normális eloszlású véletlen szám generálásával, kinyomtatjuk, és ellenőrizzük, hogy ez a szám nagyobb-e, mint 1. Csak ha ez a feltétel IGAZ lesz (lehet az első generált számmal, vagy nem), a ciklusciklus átmegy a break utasításhoz és véget ér.

Kimenet

 -0.9619334
 -0.2925257
 0.2587882
 -1.152132
 0.1957828
 0.03012394
 0.08541773
 1.11661

Ez ismét megmutatja a megfelelő megszakítási feltétel beállításának fontosságát. Ennek elmulasztása végtelen ciklushoz vezet.

Végső gondolatok

A fogalmakat elszigetelten láttuk és magyaráztuk, de a “vezérlési struktúrák” tetszés szerint kombinálhatók: A hurok tartalmazhat több belső hurkot; a feltételes szerkezetek tartalmazhatnak hurkokat és feltételes szerkezeteket, a lehetőségek végtelenek. (valójában az “Ismétlődő hurkok” áttekintésekor azt találtuk, hogy a példák egymásba ágyazott “If utasításokat” tartalmaztak).

Elég fejlett megoldásokat fejleszthetsz ki pusztán a “Vezérlési struktúrák” kombinálásával, amelyeket ebben a cikkben elmagyaráztunk. Ahogy Minsky is megállapította, egyszerűbb összetevők kölcsönhatásának eredményeként érhetünk el összetett eredményeket. A Vezérlőszerkezetek alkotják a számítástechnikai döntéshozatali folyamatok alapblokkjait. Megváltoztatják a programok áramlását, és lehetővé teszik számunkra, hogy egyszerűbb építőelemekből összetett utasításkészleteket építsünk fel.

Azt tanácsolom: ismerje meg őket.

Ez megkönnyíti a kódoláshoz és a programok megértéséhez vezető utat, és segít abban, hogy új utakat találjon a problémák megoldására.