Som definierat i detta arbete, en hjulgraf av ordningen , som ibland helt enkelt kallas ett -hjul (Harary 1994, s. 46; Pemmaraju och Skiena 2003, s. 248; Tutte 2005, s. 78), är en graf som innehåller en cykel av ordningen och för vilken varje grafvertikal i cykeln är ansluten till en annan grafvertikal som kallas nav. De kanter i ett hjul som inkluderar navet kallas ekrar (Skiena 1990, s. 146). Hjulet kan definieras som grafen join , där är singletongrafen och är cykelgrafen, vilket gör det till en -kongrafi.

Bemärk att det finns två konventioner för indexering av hjulgrafer, där vissa författare (t.ex, Gallian 2007), antar konventionen att betecknar hjulgrafen på noder.

Den tetraedriska grafen (dvs. ) är isomorf till , och är isomorf till den kompletta trepartsgrafen . I allmänhet är grafen -hjulgrafen skelettet till en -pyramid.

är en av de två grafer som erhålls genom att ta bort två kanter från pentatopgrafen , den andra grafen är hus X-grafen.

Hjulgrafer är graciösa (Frucht 1979).

Hjulgrafen har grafen dimension 2 för (och är därmed enhetsdistans) och dimension 3 i övrigt (och är därmed inte enhetsdistans) (Erdős et al. 1965, Buckley och Harary 1988).

Alla hjulgrafer är självduella grafer.

Hjulgrafer kan konstrueras i Wolframspråket med WheelGraph. Förberäknade egenskaper för ett antal hjulgrafer finns tillgängliga via GraphData.

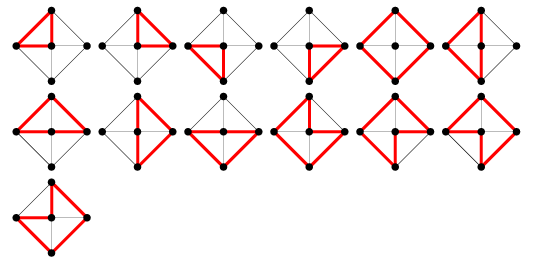
Antalet grafcykler i hjulgrafen ges av , eller 7, 13, 21, 31, 43, 57, … (OEIS A002061) för , 5, ….

I en hjulgraf har navet grad , och andra noder har grad 3. Hjulgrafer är 3-anslutna. , där är den kompletta grafen av ordning fyra. Det kromatiska talet för är

(1)

Den hjulgrafen har kromatiskt polynom

(2)