Slingor

”Loop statements” är inget annat än automatisering av flerstegsprocesser genom att organisera sekvenser av åtgärder och gruppera de delar som måste upprepas. Iteration (eller Looping) är också en central del av programmeringen och ger datorerna en stor del av deras kraft. De kan upprepa en sekvens av steg så ofta som nödvändigt, och lämpliga upprepningar av enkla steg kan lösa komplexa problem.

I allmänna termer finns det två typer av ”Looping-tekniker”:

1. ”For Loops”: är de som körs ett föreskrivet antal gånger, vilket styrs av en räknare eller ett index.
2. ”While Loops” och ”Repeat Loops”: är baserade på uppkomsten och verifieringen av ett logiskt villkor. Villkoret testas i början eller slutet av slingekonstruktionen.

Vi tar en titt på dem:

1) For Loops

I denna kontrollstruktur exekveras påståendena efter varandra i en konsekutiv ordning över en sekvens av värden som utvärderas endast när ”For Loop” initieras (aldrig omvärderad). I det här fallet är antalet iterationer fastställt och känt i förväg.

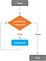
Om utvärderingen av villkoret på en variabel (som kan anta värden inom en angiven sekvens) resulterar i TRUE, kommer ett eller flera uttalanden att exekveras i sekvens över den strängen av värden. När det första villkorstestet är utfört (och resulterar i TRUE), utförs påståendet och villkoret utvärderas igen, vilket innebär en iterativ process. Delen ”variable in sequence” utför detta test på varje värde i sekvensen tills den täcker det sista elementet.

Om villkoret inte uppfylls och det resulterande resultatet är FALSK (t.ex. om delen ”variable in sequence” har gått igenom alla element i sekvensen), avslutas slingan. Om villkorstestet resulterar i FALSE i den första iterationen utförs aldrig ”For Loop”-slingan.

Syntaxen för ”For Loops” är:

Exempel 1

För att visa hur ”For Loops” fungerar skapar vi först en sekvens genom att sammanlänka olika namn på frukter för att skapa en lista (kallad ”fruit_list”):

Vi kommer att använda denna fruktlista som ”sekvens” i en ”For Loop” och låta ”For Loop” köra ett uttalande en gång (skriva ut namnet på varje värde) för varje värde i sekvensen (de olika frukterna i fruktlistan):

Så blir resultatet av ”For Loop” följande:

## "Apple"
## "Kiwi"
## "Orange"
## "Banana"

OK, så vi skrev ut namnet på varje värde i listan. Det är väl ingen stor grej, eller hur? Det som är bra är att ”For Loops” kan användas för att producera mer intressanta resultat. Ta en titt på följande exempel:

Exempel 2

Vad händer om vi vill ändra värden eller utföra beräkningar sekventiellt? Du kan använda ”For Loops” för att utföra matematiska operationer sekventiellt över varje värde i en vektor (element av samma typ, som i det här fallet kommer att vara numeriska).

I det här exemplet skapar vi en sekvens av tal (från 1 till 10) och ställer in en ”For Loop” för att beräkna och skriva ut kvadratroten av varje värde i sekvensen:

I det här fallet är resultatet av ”For Loop”:

 1
 1.414214
 1.732051
 2
 2.236068
 2.449490
 2.645751
 2.828427
 3
 3.162278

Du kan använda vilken typ av matematisk operatör som helst över en numerisk sekvens, och som vi kommer att se senare i den här artikeln kan du göra alla möjliga kombinationer mellan olika kontrollstrukturer för att nå mer komplexa resultat.

2) While Loops

I ”While Loops” utvärderas först ett villkor, och om resultatet av testningen av det villkoret är TRUE, utförs ett eller flera uttalanden upprepade gånger tills villkoret blir FALSE.

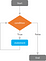
Till skillnad från ”If-utsagor”, där ett villkor som testas som SANT, exekverar ett uttryck endast en gång och slutar, är ”While Loops” iterativa utsagor som exekverar ett visst uttryck om och om igen tills villkoret blir FALSK. Om villkoret aldrig visar sig vara FALSK kommer ”While Loop” att fortsätta i all oändlighet och programmet kommer att krascha. Omvänt, om villkorstestet resulterar i FALSE i början av slingan kommer uttrycket aldrig att exekveras.

Syntaxen för ”While Loops” är:

Exempel 1

Låts oss se ett exempel. Först skapar vi en variabel (x) och tilldelar den värdet 1. Sedan ställer vi in en ”While Loop” för att iterativt testa ett villkor över den variabeln tills villkorstestet resulterar i FALSK:

Så här fungerar det: Det initiala värdet på variabeln (x) är 1, så när vi testar villkoret ”är variabeln (x) mindre än 10?”, utvärderas resultatet till TRUE och uttrycket utförs och resultatet av variabeln (x) skrivs ut, vilket i det första fallet är 1. Men sedan händer något: variabeln (x) ökas med 1 innan funktionen avslutas, och i nästa iteration kommer värdet av x att vara 2.

Denna omplacering av variabeln är viktig eftersom den så småningom kommer att nå villkoret FALSE och loopens utgång (värdet av x = 10). Om man inte ändrar de initiala villkoren i en ”While Loop” kommer det att resultera i en oändlig loop och en programkrasch.

Output

 1
 2
 3
 4
 5
 6
 7
 8
 9

Exempel 2

Har du hört talas om Fibonacci-sekvensen? Detta är en talserie med den egenskapen att nästa tal i sekvensen hittas genom att addera de två föregående talen: 0, 1, 1, 1, 2, 3, 5, 8, 13, 21,… Denna sekvens kan hittas i flera naturfenomen och har olika tillämpningar inom ekonomi, musik, arkitektur och andra discipliner.

Låt oss beräkna den med hjälp av en ”While Loop”.

I det här fallet ställer vi in ett maximalt värde i serien som stoppvillkor, så att slingan endast skriver ut Fibonacci-serien för tal som understiger 100. När ett serieelement (vilket det än är) blir större än 100 avslutas loopcykeln.

 0
 1
 1
 2
 3
 5
 8
 13
 21
 34
 55
 89

Exempel 3

Ett annat sätt att generera Fibonacci-serien med en ”While Loop” är att, i stället för att ställa in det maximala värdet i serien som ett stoppvillkor, ställa in antalet serieelement som du vill generera.

Denna ”While Loop” lägger nästa element i serien till slutet av det föregående elementet, tills man når ett stoppvillkor. I det här fallet, när serien når 10 element (oavsett vilka värden), avslutas slingan.

Output

 0 1 1 2 3 5 8 13 21 34

3) Repeat Loops

Närbesläktad med ”While Loops”, utför ”Repeat Loops” uttalanden iterativt, men tills ett stoppvillkor är uppfyllt. På så sätt utförs påståendena minst en gång, oavsett vad resultatet av villkoret är, och slingan avslutas först när ett visst villkor blir sant:

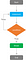
Syntaxen för ”Repeat Loops” är:

”Repeat Loops” använder ”Break statements” som stoppvillkor. ”Break statements” kombineras med testet av ett villkor för att avbryta cykler inom slingor, eftersom programmet, när det träffar ett break, kommer att lämna över kontrollen till instruktionen omedelbart efter slutet av slingan (om det finns någon).

”Repeat Loops” kommer att köras i all oändlighet om break villkoret inte är uppfyllt. Se dessa 2 exempel

Exempel 1

Först skapar vi en variabel (x) och tilldelar den värdet 5. Sedan ställer vi in en ”Repeat Loop” för att iterativt skriva ut variabelns värde, ändra variabelns värde (öka det med 1) och testa ett villkor över variabeln (om den är lika med 10) tills villkorstestet resulterar i TRUE.

”Brytningsvillkoret” utlöses när variabeln (x) når 10 och slingan avslutas.

Output

 5
 6
 7
 8
 9

Exempel 2

Vi antar nu att vi producerar en lista med slumpmässiga tal, för vilka vi inte känner till ordningen eller sekvensen för generering.

I det här exemplet kommer vi att använda en ”Repeat Loop” för att generera en sekvens av normalfördelade slumpmässiga tal (du kan generera slumpmässiga tal med vilken annan fördelning som helst, vi väljer bara denna), och bryta sekvensen så snart ett av dessa tal är större än 1. Eftersom vi inte vet vilka nummer som kommer att komma först, vet vi inte hur lång sekvensen kommer att vara: vi känner bara till brytningsvillkoret.

För det första använder vi instruktionen ”set.seed” för att fastställa de slumpmässiga numren (generera alltid samma slumpmässiga nummer), och göra detta exempel reproducerbart.

Därefter inleder vi ”Repeat Loop” genom att generera ett normalfördelat slumpmässigt tal, skriva ut det och kontrollera om talet är större än 1. Först när detta villkor blir VÄRT (kan vara med det första genererade talet eller inte) kommer loopcykeln att passera till break-anvisningen och avslutas.

Output

 -0.9619334
 -0.2925257
 0.2587882
 -1.152132
 0.1957828
 0.03012394
 0.08541773
 1.11661

Det här visar återigen på vikten av att ställa in ett korrekt brytvillkor. Om man inte gör det kommer det att resultera i en oändlig slinga.

Sluttliga tankar

Vi har sett och förklarat begrepp isolerat, men ”kontrollstrukturer” kan kombineras hur du vill: Slingor kan innehålla flera interna slingor, villkor kan innehålla slingor och villkor, alternativen är oändliga. (Faktum är att när vi granskade ”Repeat Loops” fann vi att exemplen innehöll inbäddade ”If statements”).

Du kan utveckla avancerade lösningar bara genom att kombinera de ”Control Structures” som vi förklarat i den här artikeln. Precis som Minsky konstaterade kan vi uppnå komplexa resultat som ett resultat av interaktionen mellan enklare komponenter. Kontrollstrukturer utgör grundblocken för beslutsprocesser inom databehandling. De förändrar flödet i programmen och gör det möjligt för oss att konstruera komplexa uppsättningar av instruktioner av enklare byggstenar.

Mitt råd är: lär dig om dem.

Det kommer att underlätta din väg till kodning och förståelse av program, och kommer att hjälpa dig att hitta nya sätt att lösa problem.