GeeksforGeeks
Metoden för vägd summa är en metod för beslutsfattande med flera kriterier där det finns flera alternativ och vi måste bestämma det bästa alternativet baserat på flera kriterier. Det finns andra metoder, bland annat Weighted Product Method (WPM), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, MOORA, GTMA osv. Låt oss förstå hur Weighted Sum Method fungerar med hjälp av ett exempel.
Vid ett fall där vi måste välja den bästa kandidaten bland fem kandidater som ska ställa upp på en intervju. Tabell 1 består av uppgifter om de 5 studenterna som omfattar deras CGPA, den lön som de förväntar sig per månad, deras resultat i det tekniska provet och de betyg som de uppnådde i lämplighetstestet.
Tabell 1: Exempel på datauppsättning
| Attribut | CGPA | Förväntat arvode | Resultat på tekniskt prov | Aptitude test Betyg |
|---|---|---|---|---|
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Överväg de vikter som intervjupanelen antar enligt följande:
CGPA = 30 %, förväntat stipendium = 20 %, resultat på tekniskt prov = 25 %, betyg på institutsprov = 25 %
Tabell 2: Vikterna för varje attribut
| Attribut | CGPA | Förväntat stipendium | Tekniskt provresultat | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Beneficial attribute is one in which person desires maximum values. Här är CGPA, resultat på tekniska prov och resultat på lämplighetstester fördelaktiga attribut eftersom företaget förväntar sig att studenterna ska ha fler av dessa attribut.
Inte fördelaktigt attribut är ett attribut där man önskar minimala värden. I det här fallet är det förväntade stipendiet ett icke-nyttigt attribut. Företaget hinner med personer som är villiga att arbeta mer med ett lågt stipendium.
Nu ska vi se vilken student som ska väljas ut av företaget med hjälp av Weighted Sum Method.
För detta måste vi normalisera värdena i tabell 2.
- För fördelaktiga attribut,
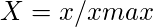
- För icke fördelaktiga attribut,
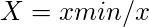
Tabell 3: Beslut om högsta värde för ett fördelaktigt attribut och lägsta värde för ett icke fördelaktigt attribut
| Attribut | CGPA | Förväntat stipendium | Resultat för teknisk examen | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | B1 |
| Student 2 | 7.6 | 8500(min) | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2(max) |
| Student 5 | 9.3(max) | 14000 | 72 | A2 |
Vi kommer att beakta följande punkter för betygssystemet
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabell 4: Uppdatering av betyg för lämplighetsprov
| Attribut | CGPA | Förväntat stipendium | Poäng för tekniskt prov | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | 3 |
| Student 2 | 7.6 | 8500(min) | 68 | 3 |
| Student 3 | 8.2 | 9500 | 63 | 2 |
| Student 4 | 8.5 | 10000 | 70 | 4(max) |
| Student 5 | 9.3(max) | 14000 | 72 | 4 |
Normalisera värdena för respektive attribut beroende på det fördelaktiga och icke fördelaktiga attributet.
Tabell 5: Normalisering
| Attribut | CGPA | Förväntat stipendium | Resultat för teknisk examen | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Student 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Student 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Student 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Student 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabell 6: Den viktnormaliserade beslutsmatrisen
| Attribut | CGPA | Förväntat stipendium | Tekniska provresultat | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.9677 | 0.7083 | 1 | 0.75 |
| Student 2 | 0.8172 | 1 | 0.9444 | 0.75 |
| Student 3 | 0.8817 | 0.8947 | 0.875 | 0.5 |
| Student 4 | 0.9134 | 0.85 | 0.9722 | 1 |
| Student 5 | 1 | 0.6071 | 1 | 1 |
Tabell 7: Multiplicering av varje parameter med respektive vikt
| Attribut | CGPA | Förväntat stipendium | Resultat av tekniskt prov | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.9677 × 0.3 | 0.7083 × 0.2 | 1 × 0.25 | 0.75 × 0.25 |
| Student 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Student 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Student 4 | 0.9134 × 0.3 | 0.85 × 0.2 | 0.9722 × 0.25 | 1 × 0,25 |
| Student 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
Tabellen ovan förenklas på följande sätt
Tabell 8: Förenklad version av tabell 7
| Attribut | CGPA | Förväntat stipendium | Teknisk examenresultat | Aptitude Test Grade |
|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 |
| Student 5 | 0.3 | 0.12142 | 0.25 | 0.25 |
Vi måste addera komponenterna i varje rad och beräkna den viktade summan som är resultatpoängen och ge prioriteringarna till eleverna
Tabell 9: Beräkning av rangordning av rangordning av studenter efter prestationspoäng
| Attribut | CGPA | Förväntat stipendium | Poäng för tekniskt prov | Poäng för lämplighetsprov | Prestationspoäng | Rank |
|---|---|---|---|---|---|---|
| Vikt | 0.3 | 0.2 | 0.25 | 0.25 | ||
| Student 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 | 0.86947 | 3 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 | 0.86876 | 4 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Student 5 | 0.3 | 0.12142 | 0.25 | 0.25 | 0.92142 | 2 |
Slutsats : Utifrån den viktade summa-metoden har det bestämts att elev 4 är det bästa valet bland de andra.