Wie in dieser Arbeit definiert, ein Radgraph der Ordnung , manchmal einfach -Rad genannt (Harary 1994, p. 46; Pemmaraju und Skiena 2003, S. 248; Tutte 2005, S. 78), ist ein Graph, der einen Zyklus der Ordnung enthält und bei dem jeder Graphknoten im Zyklus mit einem anderen Graphknoten verbunden ist, der als Nabe bezeichnet wird. Die Kanten eines Rades, die die Nabe einschließen, werden Speichen genannt (Skiena 1990, S. 146). Das Rad kann als Graphenverbindung definiert werden, wobei der Singleton-Graph und der Zyklus-Graph ist, was ihn zu einem -Kegel-Graphen macht.

Es gibt zwei Konventionen für die Indizierung von Rad-Graphen, wobei einige Autoren (z.B., Gallian 2007) nehmen die Konvention an, dass den Radgraphen auf Knoten bezeichnet.

Der Tetraeder-Graph (d.h. ) ist isomorph zu , und ist isomorph zum vollständigen dreiteiligen Graphen . Im Allgemeinen ist der -Rad-Graph das Skelett einer -Pyramide.

ist einer der beiden Graphen, die man erhält, wenn man zwei Kanten aus dem Pentatop-Graphen entfernt, der andere ist der Haus-X-Graph.

Rad-Graphen sind anmutig (Frucht 1979).

Der Radgraph hat für die Graphendimension 2 (und ist damit eindimensional) und ansonsten die Dimension 3 (und damit nicht eindimensional) (Erdős et al. 1965, Buckley und Harary 1988).

Jeder Radgraph ist ein selbstdualer Graph.

Radgraphen können in der Wolfram Language mit WheelGraph konstruiert werden. Vorberechnete Eigenschaften einer Reihe von Radgraphen sind über GraphData verfügbar.

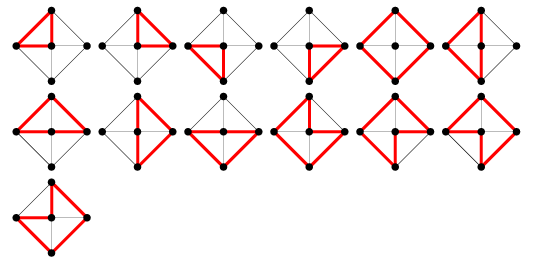
Die Anzahl der Graphzyklen im Radgraphen ist gegeben durch , oder 7, 13, 21, 31, 43, 57, … (OEIS A002061) für , 5, ….

In einem Radgraphen hat die Nabe den Grad , und andere Knoten haben den Grad 3. Radgraphen sind 3-verbunden. , wobei der vollständige Graph der Ordnung 4 ist. Die chromatische Zahl von ist

(1)

Der Radgraph hat das chromatische Polynom

(2)