Die logistische Regression, auch bekannt als binäres Logit und binäre logistische Regression, ist eine besonders nützliche Technik zur Vorhersage von Modellen. Sie wird verwendet, um Ergebnisse vorherzusagen, die zwei Optionen beinhalten, z. B. ob man gewählt oder nicht gewählt hat. Im Folgenden werde ich versuchen, einfach zu erklären, was die Gewichte bedeuten, wenn man sie für Interpretationen verwendet.

Die Interpretation der Gewichte in der logistischen Regression unterscheidet sich von der Interpretation der Gewichte in der linearen Regression, da das Ergebnis in der logistischen Regression eine Wahrscheinlichkeit zwischen 0 und 1 ist. Die Gewichte beeinflussen die Wahrscheinlichkeit nicht mehr linear. Die gewichtete Summe wird durch die logistische Funktion in eine Wahrscheinlichkeit umgewandelt. Daher müssen wir die Gleichung für die Interpretation so umformulieren, dass nur der lineare Term auf der rechten Seite der Formel steht.

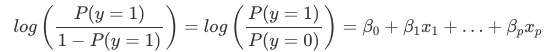
Wir nennen den Term in der log()-Funktion „Odds“ (Wahrscheinlichkeit des Ereignisses geteilt durch die Wahrscheinlichkeit, dass kein Ereignis eintritt) und in den Logarithmus eingepackt heißt er log odds.

Diese Formel zeigt, dass das logistische Regressionsmodell ein lineares Modell für die log odds ist. Na toll! Das klingt nicht gerade hilfreich! Mit einer kleinen Umstellung der Terme kann man herausfinden, wie sich die Vorhersage ändert, wenn eines der Merkmale xjxj um 1 Einheit geändert wird. Dazu können wir zunächst die Funktion exp() auf beide Seiten der Gleichung anwenden:

Dann vergleichen wir, was passiert, wenn wir einen der Merkmalswerte um 1 erhöhen. Aber anstatt die Differenz zu betrachten, betrachten wir das Verhältnis der beiden Vorhersagen:

Wir wenden die folgende Regel an:

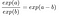
Und wir entfernen viele Begriffe:

Am Ende haben wir etwas so einfaches wie exp() eines Merkmalsgewichts. Eine Veränderung eines Merkmals um eine Einheit verändert das Odds Ratio (multiplikativ) um den Faktor exp(βj)exp(βj). Wir könnten dies auch so interpretieren: Eine Änderung von xjxj um eine Einheit erhöht das log Odds Ratio um den Wert des entsprechenden Gewichts. Die meisten Menschen interpretieren das Odds Ratio, weil das Nachdenken über den log() von etwas bekanntermaßen schwer für das Gehirn ist. Die Interpretation des Odds Ratio ist schon etwas gewöhnungsbedürftig. Wenn man zum Beispiel eine Odds von 2 hat, bedeutet das, dass die Wahrscheinlichkeit für y=1 doppelt so hoch ist wie für y=0. Wenn man eine Gewichtung (= log Odds Ratio) von 0,7 hat, dann multipliziert eine Erhöhung des jeweiligen Merkmals um eine Einheit die Odds mit exp(0,7) (ungefähr 2) und die Odds ändern sich auf 4. Aber normalerweise beschäftigt man sich nicht mit den Odds und interpretiert die Gewichte nur als Odds Ratios. Denn um die Odds tatsächlich zu berechnen, müsste man für jedes Merkmal einen Wert festlegen, was nur dann Sinn macht, wenn man eine bestimmte Instanz des Datensatzes betrachten will.

Das sind die Interpretationen für das logistische Regressionsmodell mit verschiedenen Merkmalstypen:

• Numerisches Merkmal: Erhöht man den Wert des Merkmals xjxj um eine Einheit, ändern sich die geschätzten Odds um den Faktor exp(βj)exp(βj)
• Binäres kategoriales Merkmal: Einer der beiden Werte des Merkmals ist die Referenzkategorie (in manchen Sprachen die mit 0 kodierte). Die Änderung des Merkmals xjxj von der Referenzkategorie zur anderen Kategorie ändert die geschätzte Quote um einen Faktor von exp(βj)exp(βj).
• Kategoriales Merkmal mit mehr als zwei Kategorien: Eine Lösung für den Umgang mit mehreren Kategorien ist die One-Hot-Codierung, d.h. jede Kategorie hat ihre eigene Spalte. Für ein kategoriales Merkmal mit L Kategorien braucht man nur L-1 Spalten, sonst ist es überparametrisiert. Die L-te Kategorie ist dann die Referenzkategorie. Sie können jede andere Kodierung verwenden, die in der linearen Regression verwendet werden kann. Die Interpretation für jede Kategorie entspricht dann der Interpretation von binären Merkmalen.
• Intercept β0β0: Wenn alle numerischen Merkmale Null sind und die kategorialen Merkmale der Referenzkategorie entsprechen, sind die geschätzten Odds exp(β0)exp(β0). Die Interpretation des Intercept-Gewichts ist normalerweise nicht relevant.