GeeksforGeeks
Die gewichtete Summenmethode ist eine Multikriterien-Entscheidungsmethode, bei der es mehrere Alternativen gibt und wir die beste Alternative auf der Grundlage mehrerer Kriterien bestimmen müssen. Es gibt noch weitere Methoden wie die Weighted Product Method (WPM), die Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, MOORA, GTMA usw. Die Methode der gewichteten Summe soll anhand eines Beispiels erläutert werden.
Betrachten wir einen Fall, in dem wir den besten Kandidaten unter 5 Kandidaten auswählen müssen, die zu einem Vorstellungsgespräch erscheinen. Tabelle 1 enthält die Daten von 5 Studenten, darunter ihren Notendurchschnitt, das Gehalt, das sie pro Monat erwarten, ihre Ergebnisse in der technischen Prüfung und die Noten, die sie im Eignungstest erreicht haben.
Tabelle 1: Beispieldatensatz
| Attribut | CGPA | Erwartetes Stipendium | Ergebnis der technischen Prüfung | Eignungstest Note |
|---|---|---|---|---|
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Schüler 3 | 8.2 | 9500 | 63 | B2 |
| Schüler 4 | 8.5 | 10000 | 70 | A2 |
| Schüler 5 | 9.3 | 14000 | 72 | A2 |
Betrachten Sie die Gewichte, die von der Befragungsgruppe wie folgt angenommen werden:
CGPA = 30%, Erwartetes Stipendium = 20%, Fachprüfungsnote = 25%, Eignungsprüfungsnote = 25%
Tabelle 2: Die Gewichtung der einzelnen Attribute
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Teilnehmer 1 | 9 | 12000 | 72 | B1 |
| Teilnehmer 2 | 7.6 | 8500 | 68 | B1 |
| Schüler 3 | 8.2 | 9500 | 63 | B2 |
| Schüler 4 | 8.5 | 10000 | 70 | A2 |
| Schüler 5 | 9.3 | 14000 | 72 | A2 |
Nützliches Attribut ist eines, bei dem die Person sich maximale Werte wünscht. In diesem Fall sind der Notendurchschnitt, das Ergebnis der technischen Prüfung und das Ergebnis des Eignungstests vorteilhafte Attribute, da das Unternehmen von den Studenten erwartet, dass sie mehr dieser Attribute aufweisen.
Nicht vorteilhafte Attribute sind solche, bei denen Mindestwerte gewünscht werden. In diesem Fall ist das erwartete Stipendium ein nicht-vorteilhaftes Attribut. Das Unternehmen wählt Personen, die bereit sind, mehr zu arbeiten, mit einem niedrigen Stipendium aus.
Nun wollen wir sehen, welcher Student vom Unternehmen ausgewählt werden soll, indem wir die Methode der gewichteten Summe anwenden.
Dazu müssen wir die Werte in Tabelle 2 normalisieren.
- Für vorteilhafte Attribute,
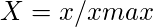
- Für nicht vorteilhafte Attribute,
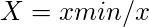
Tabelle 3: Festlegung des Höchstwertes für ein förderliches Attribut und des Mindestwertes für ein nicht förderliches Attribut
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Teilnehmer 1 | 9 | 12000 | 72(max) | B1 |
| Teilnehmer 2 | 7.6 | 8500(min) | 68 | B1 |
| Schüler 3 | 8.2 | 9500 | 63 | B2 |
| Schüler 4 | 8.5 | 10000 | 70 | A2(max) |
| Schüler 5 | 9.3(max) | 14000 | 72 | A2 |
Wir werden die folgenden Punkte für das Notensystem berücksichtigen
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabelle 4: Aktualisierung der Eignungsprüfungsnoten
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungsprüfungsnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Teilnehmer 1 | 9 | 12000 | 72(max) | 3 |
| Teilnehmer 2 | 7.6 | 8500(min) | 68 | 3 |
| Teilnehmer 3 | 8.2 | 9500 | 63 | 2 |
| Teilnehmer 4 | 8.5 | 10000 | 70 | 4(max) |
| Schüler 5 | 9.3(max) | 14000 | 72 | 4 |
Normieren Sie die Werte für das jeweilige Attribut in Abhängigkeit vom begünstigten und nicht begünstigten Attribut.
Tabelle 5: Normalisierung
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Schüler 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Schüler 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Schüler 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Schüler 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Schüler 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabelle 6: Die gewichtsnormierte Entscheidungsmatrix
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Schüler 1 | 0.9677 | 0.7083 | 1 | 0.75 |
| Teilnehmer 2 | 0.8172 | 1 | 0.9444 | 0.75 |
| Teilnehmer 3 | 0.8817 | 0.8947 | 0.875 | 0.5 |
| Teilnehmer 4 | 0.9134 | 0.85 | 0.9722 | 1 |
| Teilnehmer 5 | 1 | 0.6071 | 1 | 1 |
Tabelle 7: Multiplikation der einzelnen Parameter mit den jeweiligen Gewichten
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Schüler 1 | 0.9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Schüler 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Schüler 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Schüler 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0,25 |
| Schüler 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
Die obige Tabelle wird wie folgt vereinfacht
Tabelle 8: Vereinfachte Version von Tabelle 7
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Schüler 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 |
| Teilnehmer 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 |
| Teilnehmer 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Teilnehmer 4 | 0.27402 | 0.17 | 0.24305 | 0.25 |
| Schüler 5 | 0.3 | 0.12142 | 0.25 | 0.25 |
Wir müssen die Komponenten in jeder Zeile addieren und die gewichtete Summe berechnen, die die Leistungsnote darstellt, und den Schülern die Prioritäten zuweisen
Tabelle 9: Berechnung der Rangfolge der Studenten nach Leistungspunkten
| Attribut | CGPA | Erwartetes Stipendium | Technische Prüfungsnote | Eignungstestnote | Leistungsnote | Rang |
|---|---|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 | ||
| Schüler 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 | 0.86947 | 3 |
| Student 2 | 0.24516 | 0.2 | 0.2361 | 0.1875 | 0.86876 | 4 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 |
| Teilnehmer 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Schüler 5 | 0.3 | 0.12142 | 0.25 | 0,25 | 0,92142 | 2 |
Schlussfolgerung : Aus der Methode der gewichteten Summe ergibt sich, dass Schüler 4 die beste Wahl unter den anderen ist.