Essential Programming | Control Structures
Loops
„Schleifenanweisungen“ sind nichts anderes als die Automatisierung von mehrstufigen Prozessen durch die Organisation von Handlungsabläufen und die Gruppierung der Teile, die wiederholt werden müssen. Die Iteration (oder Schleife) ist auch ein zentraler Bestandteil der Programmierung und verleiht Computern einen Großteil ihrer Leistungsfähigkeit. Sie können eine Folge von Schritten so oft wie nötig wiederholen, und durch geeignete Wiederholungen einfacher Schritte können komplexe Probleme gelöst werden.
Im Allgemeinen gibt es zwei Arten von „Schleifentechniken“:
- „For-Schleifen“: sind solche, die eine bestimmte Anzahl von Malen ausgeführt werden, gesteuert durch einen Zähler oder einen Index.
- „While-Schleifen“ und „Repeat-Schleifen“: basieren auf dem Beginn und der Überprüfung einer logischen Bedingung. Die Bedingung wird am Anfang oder am Ende des Schleifenkonstrukts getestet.
Schauen wir uns diese Schleifen an:
1) For-Schleifen
In dieser Kontrollstruktur werden Anweisungen nacheinander in einer fortlaufenden Reihenfolge über eine Folge von Werten ausgeführt, die nur ausgewertet wird, wenn die „For-Schleife“ eingeleitet wird (niemals neu ausgewertet). In diesem Fall ist die Anzahl der Iterationen fest und im Voraus bekannt.
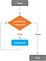
Wenn die Auswertung der Bedingung für eine Variable (die Werte innerhalb einer bestimmten Folge annehmen kann) den Wert TRUE ergibt, werden eine oder mehrere Anweisungen nacheinander über diese Folge von Werten ausgeführt. Sobald der erste Bedingungstest abgeschlossen ist (und TRUE ergibt), wird die Anweisung ausgeführt und die Bedingung erneut ausgewertet, wobei ein iterativer Prozess durchlaufen wird. Der Abschnitt „Variable in Sequenz“ führt diesen Test für jeden Wert der Sequenz durch, bis er das letzte Element erfasst.
Wenn die Bedingung nicht erfüllt ist und das Ergebnis FALSE ist (z.B. wenn der Teil „Variable in Sequenz“ alle Elemente der Sequenz durchlaufen hat), endet die Schleife. Wenn der Bedingungstest bei der ersten Iteration FALSE ergibt, wird die „For-Schleife“ nie ausgeführt.
Die Syntax von „For-Schleifen“ ist:

Beispiel 1
Um zu zeigen, wie „For-Schleifen“ funktionieren, erstellen wir zunächst eine Sequenz, indem wir verschiedene Namen von Früchten zu einer Liste (genannt „fruit_list“) verketten:

Wir verwenden diese Fruchtliste als „Sequenz“ in einer „For-Schleife“ und lassen die „For-Schleife“ für jeden angegebenen Wert in der Sequenz (die verschiedenen Früchte in der Fruchtliste) einmal eine Anweisung ausführen (den Namen jedes Wertes drucken):

Das Ergebnis der „For-Schleife“ sieht dann wie folgt aus:
## "Apple"
## "Kiwi"
## "Orange"
## "Banana"
OK, wir haben also den Namen jedes Wertes in der Liste gedruckt. Keine große Sache, oder? Das Gute ist, dass „For-Schleifen“ verwendet werden können, um interessantere Ergebnisse zu erzielen. Schauen Sie sich das folgende Beispiel an:
Beispiel 2
Was, wenn wir Werte ändern oder Berechnungen nacheinander durchführen wollen? Sie können „For-Schleifen“ verwenden, um mathematische Operationen sequentiell über jeden Wert eines Vektors (Elemente desselben Typs, in diesem Fall numerisch) durchzuführen.
In diesem Beispiel erstellen wir eine Folge von Zahlen (von 1 bis 10) und setzen eine „For-Schleife“ ein, um die Quadratwurzel jedes Wertes in dieser Folge zu berechnen und zu drucken:

In diesem Fall ist das Ergebnis der „For-Schleife“:
1
1.414214
1.732051
2
2.236068
2.449490
2.645751
2.828427
3
3.162278
Sie können jede Art von mathematischem Operator über eine numerische Folge verwenden und, wie wir später in diesem Artikel sehen werden, alle möglichen Kombinationen zwischen verschiedenen Kontrollstrukturen vornehmen, um komplexere Ergebnisse zu erzielen.
2) While-Schleifen
In „While-Schleifen“ wird zunächst eine Bedingung ausgewertet, und wenn das Ergebnis der Prüfung dieser Bedingung WAHR ist, werden eine oder mehrere Anweisungen wiederholt ausgeführt, bis diese Bedingung FALSCH wird.
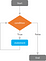
Im Gegensatz zu „If-Anweisungen“, bei denen eine als WAHR getestete Bedingung einen Ausdruck nur einmal ausführt und beendet, sind „While-Schleifen“ iterative Anweisungen, die einen Ausdruck immer wieder ausführen, bis die Bedingung FALSCH wird. Wenn die Bedingung niemals FALSCH wird, läuft die „While-Schleife“ ewig weiter und das Programm stürzt ab. Umgekehrt, wenn der Bedingungstest am Anfang der Schleife FALSE ergibt, wird der Ausdruck nie ausgeführt.
Die Syntax von „While-Schleifen“ ist:

Beispiel 1
Lassen Sie uns ein Beispiel sehen. Zuerst erstellen wir eine Variable (x) und weisen ihr den Wert 1 zu. Dann setzen wir eine „While-Schleife“ ein, um iterativ eine Bedingung über diese Variable zu testen, bis das Ergebnis des Bedingungstests FALSCH ist:

So funktioniert es: Der Anfangswert der Variablen (x) ist 1, wenn wir also die Bedingung „Ist die Variable (x) kleiner als 10?Wenn wir also die Bedingung „Ist die Variable (x) kleiner als 10?“ testen, wird das Ergebnis zu TRUE ausgewertet und der Ausdruck wird ausgeführt, wobei das Ergebnis der Variable (x) gedruckt wird, das im ersten Fall 1 ist. Aber dann passiert etwas: Die Variable (x) wird um 1 erhöht, bevor die Funktion endet, und in der nächsten Iteration wird der Wert von x 2 sein.
Diese Neuzuweisung der Variablen ist wichtig, weil sie schließlich die FALSE-Bedingung und den Schleifenausgang (Wert von x = 10) erreichen wird. Werden die Anfangsbedingungen in einer „While-Schleife“ nicht geändert, führt dies zu einer Endlosschleife und einem Programmabsturz.
Ausgabe
1
2
3
4
5
6
7
8
9
Beispiel 2
Haben Sie schon einmal von der Fibonacci-Folge gehört? Das ist eine Zahlenreihe, die die Eigenschaft hat, dass die nächste Zahl in der Reihe durch die Addition der beiden vorhergehenden Zahlen gefunden wird: 0, 1, 1, 2, 3, 5, 8, 13, 21,… Diese Reihe findet sich in verschiedenen Naturphänomenen und hat verschiedene Anwendungen in der Finanzwelt, Musik, Architektur und anderen Disziplinen.
Berechnen wir sie mit einer „While-Schleife“.

In diesem Fall setzen wir einen Maximalwert in der Reihe als Stoppbedingung, so dass die Schleife die Fibonacci-Reihe nur für Zahlen unter 100 ausgibt. Wenn ein Reihenelement (welches auch immer es ist) größer als 100 wird, endet der Schleifenzyklus.
0
1
1
2
3
5
8
13
21
34
55
89
Beispiel 3
Eine andere Möglichkeit, die Fibonacci-Reihe mit einer „While-Schleife“ zu erzeugen, besteht darin, statt den Maximalwert der Reihe als Stopp-Bedingung zu setzen, die Anzahl der Reihenelemente festzulegen, die erzeugt werden sollen.

Diese „While-Schleife“ hängt das nächste Element der Serie an das Ende des vorherigen Elements an, bis eine Stoppbedingung erreicht ist. In diesem Fall endet die Schleife, wenn die Reihe 10 Elemente erreicht (egal welche Werte).
Ausgabe
0 1 1 2 3 5 8 13 21 34
3) Wiederholungsschleifen
In enger Verbindung mit „While-Schleifen“ führen „Repeat-Schleifen“ Anweisungen iterativ aus, jedoch bis eine Stopp-Bedingung erfüllt ist. Auf diese Weise werden die Anweisungen mindestens einmal ausgeführt, unabhängig vom Ergebnis der Bedingung, und die Schleife wird erst verlassen, wenn eine bestimmte Bedingung WAHR wird:
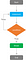
Die Syntax von „Wiederholungsschleifen“ ist:

„Wiederholungsschleifen“ verwenden „Break-Anweisungen“ als Stoppbedingung. „Break-Anweisungen“ werden mit dem Test einer Bedingung kombiniert, um Zyklen innerhalb von Schleifen zu unterbrechen, da das Programm, wenn es auf eine Unterbrechung stößt, die Kontrolle an die Anweisung unmittelbar nach dem Ende der Schleife (falls vorhanden) übergibt.
„Wiederholungsschleifen“ laufen ewig, wenn die Unterbrechungsbedingung nicht erfüllt ist. Siehe diese 2 Beispiele
Beispiel 1
Zuerst erstellen wir eine Variable (x) und weisen ihr den Wert 5 zu. Dann setzen wir eine „Wiederholungsschleife“, um iterativ den Wert der Variablen zu drucken, den Wert der Variablen zu ändern (um 1 zu erhöhen) und eine Bedingung über diese Variable zu testen (wenn sie gleich 10 ist), bis der Bedingungstest TRUE ergibt.

Die „Abbruchbedingung“ wird ausgelöst, wenn die Variable (x) 10 erreicht, und die Schleife endet.
Ausgabe
5
6
7
8
9
Beispiel 2
Angenommen, wir erzeugen eine Liste von Zufallszahlen, deren Reihenfolge wir nicht kennen.
In diesem Beispiel verwenden wir eine „Wiederholungsschleife“, um eine Folge normalverteilter Zufallszahlen zu erzeugen (Sie können Zufallszahlen mit jeder anderen Verteilung erzeugen, wir wählen nur diese), und brechen die Folge ab, sobald eine dieser Zahlen größer als 1 ist. Da wir nicht wissen, welche Zahlen zuerst kommen, wissen wir auch nicht, wie lang die Folge sein wird: wir kennen nur die Abbruchbedingung.

Zunächst verwenden wir die Anweisung „set.seed“, um die Zufallszahlen zu fixieren (immer die gleichen Zufallszahlen zu erzeugen) und dieses Beispiel reproduzierbar zu machen.
Dann starten wir die „Wiederholungsschleife“, indem wir eine normalverteilte Zufallszahl erzeugen, sie ausdrucken und prüfen, ob diese Zahl größer als 1 ist. Nur wenn diese Bedingung WAHR wird (das kann bei der ersten erzeugten Zahl der Fall sein oder auch nicht), geht der Schleifenzyklus zur Break-Anweisung über und endet.
Ausgabe
-0.9619334
-0.2925257
0.2587882
-1.152132
0.1957828
0.03012394
0.08541773
1.11661
Dies zeigt wieder einmal, wie wichtig es ist, eine richtige Abbruchbedingung zu setzen. Andernfalls entsteht eine Endlosschleife.
Abschließende Überlegungen
Wir haben die Konzepte isoliert betrachtet und erklärt, aber „Kontrollstrukturen“ können beliebig kombiniert werden: Schleifen können mehrere interne Schleifen enthalten; Konditionale können Schleifen und Konditionale enthalten, die Möglichkeiten sind endlos. (Tatsächlich haben wir bei der Überprüfung von „Wiederholungsschleifen“ festgestellt, dass die Beispiele verschachtelte „Wenn-Anweisungen“ enthalten).
Sie können fortgeschrittene Lösungen entwickeln, indem Sie einfach die „Kontrollstrukturen“ kombinieren, die wir in diesem Artikel erklärt haben. Wie Minsky feststellte, können wir komplexe Ergebnisse als Ergebnis der Interaktion einfacher Komponenten erreichen. Kontrollstrukturen sind die Grundbausteine für Entscheidungsprozesse in der Datenverarbeitung. Sie verändern den Ablauf von Programmen und ermöglichen es uns, komplexe Befehlssätze aus einfacheren Bausteinen zu konstruieren.
Mein Rat ist: Lernen Sie sie kennen.
Es wird Ihnen den Weg zum Programmieren und zum Verständnis von Programmen erleichtern und Ihnen helfen, neue Wege zur Lösung von Problemen zu finden.