Jak je definováno v této práci, kolový graf řádu , někdy jednoduše nazývaný kolový (Harary 1994, str. 46; Pemmaraju a Skiena 2003, s. 248; Tutte 2005, s. 78), je graf, který obsahuje cyklus řádu a u něhož je každý vrchol grafu v cyklu spojen s jedním jiným vrcholem grafu známým jako náboj. Hrany kola, které zahrnují náboj, se nazývají špice (Skiena 1990, s. 146). Kolo lze definovat jako spojení grafů , kde je singletonový graf a je graf cyklu, což z něj dělá -kuželový graf.

Všimněte si, že existují dvě konvence pro indexování grafů kol, přičemž někteří autoři (např, Gallian 2007), přijímají konvenci, že označuje kolový graf na uzlech.

Čtyřstěnný graf (tj. ) je izomorfní k a je izomorfní k úplnému trojstěnnému grafu . Obecně je kolový graf kostrou pyramidy.

Je jedním ze dvou grafů získaných odstraněním dvou hran z pentatopového grafu , druhým je graf domu X.

Kolové grafy jsou půvabné (Frucht 1979).

Kolový graf má dimenzi grafu 2 pro (a je tedy jednotkově vzdálený) a dimenzi 3 v opačném případě (a tedy není jednotkově vzdálený) (Erdős et al. 1965, Buckley a Harary 1988).

Každý kolový graf je samodvojný graf.

Kolové grafy lze ve Wolframově jazyce konstruovat pomocí WheelGraph. Předpočítané vlastnosti řady kolových grafů jsou k dispozici prostřednictvím GraphData.

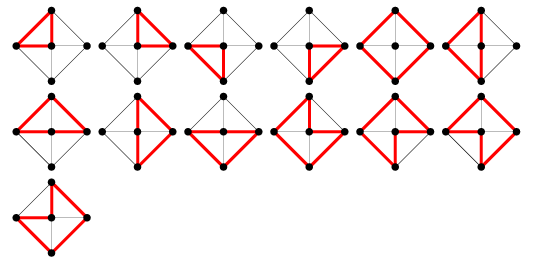
Počet cyklů grafu v kolovém grafu je dán , neboli 7, 13, 21, 31, 43, 57, … (OEIS A002061) pro , 5, ….

V kolovém grafu má náboj stupeň a ostatní uzly mají stupeň 3. Kolové grafy jsou 3spojené. , kde je úplný graf řádu čtyři. Chromatické číslo je

(1)

Př. Graf kola má chromatický polynom

(2)

.