Logistická regrese, známá také jako binární logit a binární logistická regrese, je obzvláště užitečná technika prediktivního modelování. Používá se k předpovídání výsledků zahrnujících dvě možnosti, například zda jste volili, nebo nevolili. Níže se pokusím pouze vysvětlit, co znamenají váhy při jejich použití pro interpretaci.

Interpretace vah v logistické regresi se liší od interpretace vah v lineární regresi, protože výsledkem v logistické regresi je pravděpodobnost mezi 0 a 1. Váhy již neovlivňují pravděpodobnost lineárně. Součet vah je transformován logistickou funkcí na pravděpodobnost. Proto musíme rovnici pro interpretaci přeformulovat tak, aby na pravé straně vzorce byl pouze lineární člen.

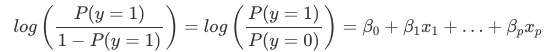
Člen ve funkci log() nazýváme „šance“ (pravděpodobnost události dělená pravděpodobností žádné události) a zabalený do logaritmu se nazývá log šance.

Tento vzorec ukazuje, že model logistické regrese je lineárním modelem pro log šance. Skvělé! To nezní užitečně! S trochou promíchání výrazů můžete zjistit, jak se změní předpověď, když se jedna z funkcí xjxj změní o 1 jednotku. K tomu můžeme nejprve použít funkci exp() na obě strany rovnice:

Poté porovnáme, co se stane, když zvýšíme hodnotu jednoho z rysů o 1. V případě, že se hodnota jednoho z rysů zvýší o 1, můžeme použít funkci exp(). Místo rozdílu se však podíváme na poměr obou předpovědí:

Použijeme následující pravidlo:

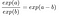
A odstraníme mnoho výrazů:

Na konci máme něco tak jednoduchého jako exp() váhy funkce. Změna funkce o jednu jednotku změní poměr šancí (multiplikativně) o faktor exp(βj)exp(βj). Mohli bychom to také interpretovat tímto způsobem: Změna xjxj o jednu jednotku zvyšuje logaritmický poměr šancí o hodnotu příslušné váhy. Většina lidí interpretuje poměr šancí, protože je známo, že přemýšlet o log() něčeho je pro mozek náročné. Na interpretaci poměru šancí je již třeba si zvyknout. Máte-li například šanci 2, znamená to, že pravděpodobnost pro y=1 je dvakrát vyšší než pro y=0. Máte-li váhu (= logaritmický poměr šancí) 0,7, pak zvýšením příslušné funkce o jednu jednotku se šance vynásobí exp(0,7) (přibližně 2) a šance se změní na 4. Většinou se ale šancemi nezabýváte a váhy interpretujete pouze jako poměry šancí. Protože pro skutečný výpočet šancí byste museli nastavit hodnotu pro každý rys, což má smysl pouze v případě, že se chcete podívat na jeden konkrétní případ vašeho souboru dat.

Tyto jsou interpretace pro model logistické regrese s různými typy rysů:

• Číselný rys: Pokud zvýšíte hodnotu rysu xjxj o jednu jednotku, odhadovaná šance se změní o faktor exp(βj)exp(βj)
• Binární kategoriální rys: Jedna ze dvou hodnot znaku je referenční kategorie (v některých jazycích ta, která je zakódována v 0). Změna rysu xjxj z referenční kategorie na druhou kategorii změní odhadovanou pravděpodobnost o faktor exp(βj)exp(βj).
• Kategoriální rys s více než dvěma kategoriemi: Jedním z řešení, jak se vypořádat s více kategoriemi, je kódování s jedním snímkem, což znamená, že každá kategorie má svůj vlastní sloupec. Pro kategoriální rys s L kategoriemi stačí L-1 sloupců, jinak je příliš parametrizovaný. L-tá kategorie je pak referenční kategorií. Můžete použít jakékoli jiné kódování, které lze použít v lineární regresi. Interpretace pro každou kategorii je pak ekvivalentní interpretaci binárních rysů.
• Intercept β0β0: Když jsou všechny číselné rysy nulové a kategoriální rysy jsou u referenční kategorie, odhadovaná šance je exp(β0)exp(β0). Interpretace intercepční váhy obvykle není relevantní.

.