GeeksforGeeks
Metoda váženého součtu je vícekriteriální rozhodovací metoda, při které existuje více alternativ a my musíme určit nejlepší alternativu na základě více kritérií. Existují i další metody, mezi něž patří metoda váženého součinu (WPM), technika pořadí preferencí podle podobnosti s ideálním řešením (TOPSIS), VIKOR, MOORA, GTMA atd. Pochopíme fungování metody váženého součtu na příkladu.
Uvažujme případ, kdy máme vybrat nejlepšího kandidáta z 5 kandidátů, kteří se dostaví na pohovor. Tabulka 1 obsahuje údaje o 5 uchazečích, které zahrnují jejich CGPA, plat, který očekávají měsíčně, jejich výsledky v technické zkoušce a známky, kterých dosáhli v testu způsobilosti.
Tabulka 1: Vzorový soubor dat
| Příznak | CGPA | Očekávaný plat | Skóre u technické zkoušky | Zkouška způsobilosti Třída |
|---|---|---|---|---|
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Uvažujme váhy předpokládané výběrovou komisí takto :
CGPA = 30%, očekávané stipendium = 20%, skóre technické zkoušky = 25%, známka z testu Aptitute = 25%
Tabulka 2: Váhy jednotlivých atributů
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Přínosný atribut je takový, u kterého si člověk přeje maximální hodnoty. Zde jsou výhodnými atributy CGPA, výsledek technické zkoušky a výsledky testu schopností, protože společnost očekává, že studenti budou mít těchto atributů více.
Nepřínosný atribut je takový, u kterého jsou žádoucí minimální hodnoty. V tomto případě je očekávané stipendium nevýhodným atributem. Společnost vybírá lidi, kteří jsou ochotni pracovat více s nízkým stipendiem.
Nyní se podíváme, kterého studenta má společnost vybrat pomocí metody váženého součtu.
Pro to musíme hodnoty v tabulce 2 normalizovat.
- Pro prospěšné atributy
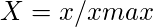
- Pro neprospěšné atributy
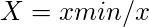
Tabulka 3: Rozhodování o maximální hodnotě pro prospěšný atribut a minimální hodnotě pro neprospěšný atribut
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | B1 |
| Student 2 | 7.6 | 8500(min) | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2(max) |
| Student 5 | 9.3(max) | 14000 | 72 | A2 |
Uvažujeme následující body pro systém známek
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabulka 4: Aktualizace známek ze zkoušky způsobilosti
| Atribut | CGPA | Předpokládané stipendium | Skóre z technické zkoušky | Známka ze zkoušky způsobilosti |
|---|---|---|---|---|
| Váha | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | 3 |
| Student 2 | 7.6 | 8500(min) | 68 | 3 |
| Student 3 | 8.2 | 9500 | 63 | 2 |
| Student 4 | 8.5 | 10000 | 70 | 4(max) |
| Student 5 | 9.3(max) | 14000 | 72 | 4 |
Normalizujte hodnoty příslušného atributu v závislosti na příznivém a nepříznivém atributu.
Tabulka 5: Normalizace
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Student 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Student 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Student 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Student 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabulka č. 6: Váhově normalizovaná rozhodovací matice
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0,9677 | 0,7083 | 1 | 0.75 |
| Student 2 | 0,8172 | 1 | 0,9444 | 0,75 |
| Student 3 | 0,8817 | 0,8947 | 0.875 | 0,5 |
| Student 4 | 0,9134 | 0,85 | 0,9722 | 1 |
| Student 5 | 1 | 0.6071 | 1 | 1 |
Tabulka 7: Vynásobení jednotlivých parametrů příslušnými váhami
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0,9677 × 0.3 | 0,7083 × 0,2 | 1 × 0,25 | 0,75 × 0,25 |
| Student 2 | 0.8172 × 0,3 | 1 × 0,2 | 0,9444 × 0,25 | 0,75 × 0,25 |
| Student 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Student 4 | 0,9134 × 0,3 | 0,85 × 0,2 | 0,9722 × 0.25 | 1 × 0,25 |
| Student 5 | 1 × 0,3 | 0,6071 × 0,2 | 1 × 0.25 | 1 × 0.25 |
Výše uvedená tabulka je zjednodušena takto
Tabulka 8: Zjednodušená verze tabulky 7
| Atribut | CGPA | Očekávané stipendium | Skóre technické zkoušky | Známka z testu schopností |
|---|---|---|---|---|
| Váha | 0.3 | 0,2 | 0,25 | 0,25 |
| Student 1 | 0.29031 | 0,14166 | 0,25 | 0,1875 |
| Student 2 | 0.24516 | 0,2 | 0,2361 | 0,1875 |
| Student 3 | 0,26451 | 0.17894 | 0,21875 | 0,125 |
| Student 4 | 0,27402 | 0,17 | 0.24305 | 0,25 |
| Student 5 | 0,3 | 0,12142 | 0,25 | 0.25 |
Musíme sečíst složky v každém řádku a vypočítat vážený součet, který je výkonnostním skóre, a udělit žákům priority
Tabulka 9: Výpočet pořadí studentů podle výkonnostního skóre
| Atribut | CGPA | Očekávané stipendium | Skóre z technické zkoušky | Známka z testu schopností | Skóre z výkonu | Příčka |
|---|---|---|---|---|---|---|
| Váha | 0.3 | 0,2 | 0,25 | 0,25 | ||
| Student 1 | 0,29031 | 0,14166 | 0,25 | 0,1875 | 0.86947 | 3 |
| Student 2 | 0,24516 | 0,2 | 0,2361 | 0.1875 | 0,86876 | 4 |
| Student 3 | 0,26451 | 0.17894 | 0,21875 | 0,125 | 0,7872 | 5 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 |
| Student 5 | 0,3 | 0,12142 | 0.25 | 0,25 | 0,92142 | 2 |
Závěr : Na základě metody váženého součtu bylo rozhodnuto, že student 4 je nejlepší volbou mezi ostatními.