Cum sunt definite în această lucrare, un graf roată de ordinul , uneori numit simplu un -roată (Harary 1994, p. 46; Pemmaraju și Skiena 2003, p. 248; Tutte 2005, p. 78), este un graf care conține un ciclu de ordinul și pentru care fiecare vârf de graf din ciclu este conectat la un alt vârf de graf cunoscut sub numele de hub. Marginile unei roți care includ butucul se numesc spițe (Skiena 1990, p. 146). Roata poate fi definită ca graful join , unde este graful singleton și este graful ciclului, ceea ce o face un graf conic.

Rețineți că există două convenții pentru indexarea grafurilor roată, unii autori (de ex, Gallian 2007), adoptând convenția că denotă graful roată pe noduri.

Graful tetraedru (adică ) este izomorf cu , iar este izomorf cu graful tripartit complet . În general, graful -roată este scheletul unei piramide .

este unul dintre cele două grafuri obținute prin eliminarea a două muchii din graful pentatopului , celălalt fiind graful casei X.

Grafurile roată sunt grațioase (Frucht 1979).

Graful roată are dimensiunea grafică 2 pentru (și, prin urmare, are distanța unitară) și dimensiunea 3 în rest (și, prin urmare, nu are distanța unitară) (Erdős et al. 1965, Buckley și Harary 1988).

Care graf de roată este un graf auto-dual.

Grafele de roată pot fi construite în limbajul Wolfram folosind WheelGraph. Proprietățile precalculate ale unui număr de grafuri cu roți sunt disponibile prin GraphData.

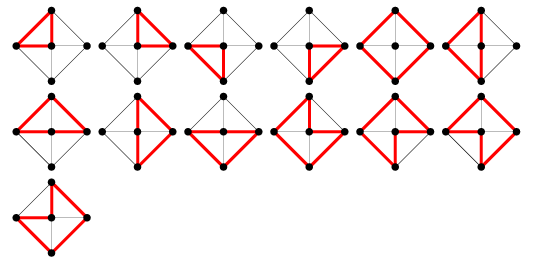
Numărul de cicluri de graf în graful cu roți este dat de , sau 7, 13, 21, 31, 43, 57, … (OEIS A002061) pentru , 5, ….

Într-un graf de roată, butucul are gradul , iar celelalte noduri au gradul 3. Grafurile de roată au 3 conexiuni. , unde este graful complet de ordinul 4. Numărul cromatic al lui este

(1)

Ceea de graficul roții are polinomul cromatic

(2)

.