Regresia logistică, cunoscută și sub numele de logit binar și regresie logistică binară, este o tehnică de modelare predictivă deosebit de utilă. Ea este utilizată pentru a prezice rezultate care implică două opțiuni, de exemplu, dacă ați votat sau nu ați votat. Mai jos voi încerca să explic doar ce înseamnă ponderile atunci când le folosiți pentru interpretări.

Interpretarea ponderilor în regresia logistică diferă de interpretarea ponderilor în regresia liniară, deoarece rezultatul în regresia logistică este o probabilitate între 0 și 1. Ponderile nu mai influențează probabilitatea în mod liniar. Suma ponderată este transformată de funcția logistică într-o probabilitate. Prin urmare, trebuie să reformulăm ecuația pentru interpretare astfel încât doar termenul liniar să se afle în partea dreaptă a formulei.

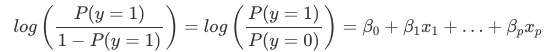
Noi numim termenul din funcția log() „cote” (probabilitatea evenimentului împărțită la probabilitatea de a nu avea niciun eveniment) și înfășurat în logaritm se numește log odds.

Această formulă arată că modelul de regresie logistică este un model liniar pentru log odds. Minunat! Asta nu pare a fi de ajutor! Cu o mică amestecare a termenilor, vă puteți da seama cum se schimbă predicția atunci când una dintre caracteristicile xjxj este modificată cu 1 unitate. Pentru a face acest lucru, putem aplica mai întâi funcția exp() la ambele părți ale ecuației:

Apoi comparăm ce se întâmplă atunci când creștem una dintre valorile caracteristicilor cu 1 unitate. Dar în loc să ne uităm la diferență, ne uităm la raportul dintre cele două predicții:

Aplicăm următoarea regulă:

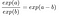
Și eliminăm mulți termeni:

În final, avem ceva la fel de simplu ca și exp() a ponderii unei caracteristici. O modificare a unei caracteristici cu o unitate modifică raportul de șanse (multiplicativ) cu un factor de exp(βj)exp(βj). Am putea, de asemenea, să o interpretăm astfel: O modificare în xjxj cu o unitate crește raportul de șanse logaritmic cu valoarea ponderii corespunzătoare. Majoritatea oamenilor interpretează raportul de șanse deoarece se știe că gândirea la log() a ceva este dificilă pentru creier. Interpretarea raportului de probabilitate necesită deja o anumită obișnuință. De exemplu, dacă aveți o probabilitate de 2, înseamnă că probabilitatea pentru y=1 este de două ori mai mare decât pentru y=0. Dacă aveți o pondere (= log odds ratio) de 0,7, atunci creșterea caracteristicii respective cu o unitate înmulțește șansele cu exp(0,7) (aproximativ 2) și șansele se schimbă la 4. Dar, de obicei, nu vă ocupați de șanse și interpretați ponderile doar ca odds ratio. Pentru că pentru a calcula efectiv cotele ar trebui să setați o valoare pentru fiecare caracteristică, ceea ce are sens doar dacă doriți să vă uitați la o instanță specifică a setului de date.

Acestea sunt interpretările pentru modelul de regresie logistică cu diferite tipuri de caracteristici:

• Caracteristică numerică: Dacă creșteți valoarea caracteristicii xjxj cu o unitate, șansele estimate se schimbă cu un factor de exp(βj)exp(βj)
• Caracteristică categorică binară: Una dintre cele două valori ale caracteristicii este categoria de referință (în unele limbi, cea codificată în 0). Schimbarea caracteristicii xjxj de la categoria de referință la cealaltă categorie modifică șansele estimate cu un factor de exp(βj)exp(βj).
• Caracteristică categorială cu mai mult de două categorii: O soluție pentru a trata mai multe categorii este one-hot-encoding, ceea ce înseamnă că fiecare categorie are propria sa coloană. Aveți nevoie doar de L-1 coloane pentru o caracteristică categorială cu L categorii, altfel aceasta este supraparametrizată. Cea de-a L-a categorie este atunci categoria de referință. Puteți utiliza orice altă codificare care poate fi utilizată în regresia liniară. Interpretarea pentru fiecare categorie este atunci echivalentă cu interpretarea caracteristicilor binare.
• Intercept β0β0: Atunci când toate caracteristicile numerice sunt zero și caracteristicile categorice sunt la categoria de referință, șansele estimate sunt exp(β0)exp(β0). Interpretarea ponderii de interceptare nu este, de obicei, relevantă.