Como definido neste trabalho, um gráfico de roda de ordem , às vezes simplesmente chamado de roda (Harary 1994, p. 46; Pemmaraju e Skiena 2003, p. 248; Tutte 2005, p. 78), é um gráfico que contém um ciclo de ordem e para o qual cada vértice do ciclo está ligado a um outro vértice do gráfico conhecido como o cubo. As arestas de uma roda que incluem o cubo são chamadas raios (Skiena 1990, p. 146). A roda pode ser definida como a união do gráfico , onde é o gráfico de um botão e é o gráfico do ciclo, tornando-o um gráfico de -cone.

Note que existem duas convenções para a indexação dos gráficos de roda, com alguns autores (e.g, Gallian 2007), adoptando a convenção que denota o gráfico da roda em nós.

O gráfico tetraédrico (i.e., ) é isomórfico para , e é isomórfico para o gráfico tripartido completo . Em geral, o gráfico -roda é o esqueleto de um – pirâmide.

é um dos dois gráficos obtidos pela remoção de duas bordas do gráfico pentatope , sendo o outro a casa X gráfico.

Gráficos de roda são graciosos (Frucht 1979).

O gráfico de roda tem a dimensão gráfica 2 para (e portanto é unidade-distância) e dimensão 3 caso contrário (e portanto não unidade-distância) (Erdős et al. 1965, Buckley and Harary 1988).

Any wheel graph is a self-dual graph.

Gráficos de roda podem ser construídos na Linguagem Wolfram usando WheelGraph. As propriedades pré-calculadas de um número de gráficos de roda estão disponíveis via GraphData.

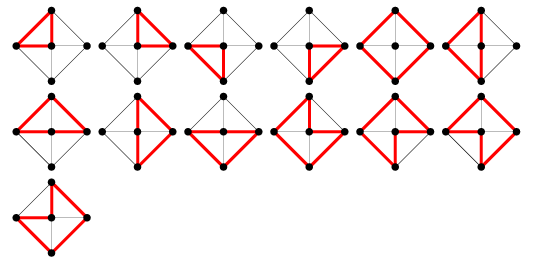
O número de ciclos de gráficos no gráfico de roda é dado por , ou 7, 13, 21, 31, 43, 57, … (OEIS A002061) para , 5, ….

Em um gráfico de roda, o cubo tem grau , e outros nós têm grau 3. Os gráficos de roda são de 3. , onde é o gráfico completo da ordem quatro. O número cromático de é

(1)

O gráfico da roda tem polinomial cromático

(2)