Como interpretar os pesos em Regressão Logística
Regessão logística, também conhecida como logit binário e regressão logística binária, é uma técnica de modelação preditiva particularmente útil. É usada para prever resultados envolvendo duas opções, se você votou ou não votou, por exemplo. Abaixo vou tentar explicar o que os pesos significam quando você os usa para interpretações.
A interpretação dos pesos na regressão logística difere da interpretação dos pesos na regressão linear, já que o resultado na regressão logística é uma probabilidade entre 0 e 1. Os pesos não influenciam mais a probabilidade linearmente. A soma ponderada é transformada pela função logística para uma probabilidade. Portanto precisamos reformular a equação para a interpretação de modo que apenas o termo linear esteja do lado direito da fórmula.
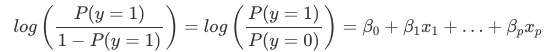
Chamaemos o termo na função log() de “odds” (probabilidade de evento dividida pela probabilidade de nenhum evento) e envolto no logaritmo é chamado de log odds.
Esta fórmula mostra que o modelo de regressão logística é um modelo linear para as probabilidades logísticas. Ótimo! Isso não soa útil! Com um pequeno embaralhamento dos termos, você pode descobrir como a previsão muda quando uma das características xjxj é alterada por 1 unidade. Para fazer isso, podemos primeiro aplicar a função exp() a ambos os lados da equação:

Em seguida, comparamos o que acontece quando aumentamos um dos valores das características em 1. Mas em vez de olharmos para a diferença, olhamos para a razão das duas previsões:

Aplicamos a seguinte regra:
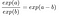
E removemos muitos termos:

No final, temos algo tão simples como exp() de um peso de característica. Uma alteração de uma característica por uma unidade altera o odds ratio (multiplicativo) por um factor de exp(βj)exp(βj). Poderíamos também interpretá-lo desta forma: Uma alteração no xjxj por uma unidade aumenta o odds ratio de log pelo valor do peso correspondente. A maioria das pessoas interpreta o odds ratio porque pensar no log() de algo é conhecido por ser difícil para o cérebro. Interpretar o odds ratio já requer que alguns se acostumem a fazê-lo. Por exemplo, se você tem odds ratio de 2, significa que a probabilidade para y=1 é duas vezes maior que y=0. Se você tem um peso (= log odds ratio) de 0,7, então aumentar a respectiva característica por uma unidade multiplica as odds por exp(0,7) (aproximadamente 2) e as odds mudam para 4. Mas normalmente você não lida com as odds e interpreta os pesos apenas como os odds ratio. Porque para realmente calcular as probabilidades você precisaria definir um valor para cada característica, o que só faz sentido se você quiser olhar para uma instância específica do seu conjunto de dados.
Estas são as interpretações para o modelo de regressão logística com diferentes tipos de características:
- Função numérica: Se você aumentar o valor da característica xjxj em uma unidade, as probabilidades estimadas mudam por um fator de exp(βj)exp(βj)
- Característica categórica binária: Um dos dois valores da característica é a categoria de referência (em alguns idiomas, a codificada em 0). Alterar a característica xjxj da categoria de referência para a outra categoria altera as probabilidades estimadas por um factor de exp(βj)exp(βj).
- Característica categórica com mais de duas categorias: Uma solução para lidar com múltiplas categorias é a codificação de um ponto, o que significa que cada categoria tem a sua própria coluna. Você só precisa de colunas L-1 para uma característica categórica com categorias L, caso contrário ela é super-parametrizada. A L-ésima categoria é então a categoria de referência. Você pode usar qualquer outra codificação que possa ser usada em regressão linear. A interpretação para cada categoria então é equivalente à interpretação das características binárias.
- Intercept β0β0: Quando todas as características numéricas são zero e as características categóricas estão na categoria de referência, as probabilidades estimadas são exp(β0)exp(β0). A interpretação do peso da intercepção geralmente não é relevante.