Zoals in dit werk gedefinieerd, een wielgrafiek van orde , soms eenvoudigweg een -wiel genoemd (Harary 1994, p. 46; Pemmaraju en Skiena 2003, p. 248; Tutte 2005, p. 78), is een grafiek die een cyclus van orde bevat en waarvoor elk grafiekvertex in de cyclus verbonden is met één ander grafiekvertex, bekend als de hub. De ribben van een wiel die de naaf omvatten worden spaken genoemd (Skiena 1990, p. 146). Het wiel kan worden gedefinieerd als de grafiek join , waarbij de singleton-grafiek is en de cyclus-grafiek, waardoor het een -kegel-grafiek is.

Merk op dat er twee conventies zijn voor de indexering voor wiel-grafieken, waarbij sommige auteurs (bijv, Gallian 2007), nemen de conventie aan dat de wielgrafiek op knopen aanduidt.

De tetrahedrale grafiek (d.w.z. ) isomorf met , en isomorf met de volledige tripartiete grafiek . In het algemeen is de -wielgrafiek het skelet van een -piramide.

is een van de twee grafieken die verkregen worden door twee ribben te verwijderen uit de pentatopegrafiek , de andere is de huis X-grafiek.

Wielgrafieken zijn sierlijk (Frucht 1979).

De wielgrafiek heeft grafiekdimensie 2 voor (en is dus eenheidsafstand) en dimensie 3 anders (en is dus geen eenheidsafstand) (Erdős et al. 1965, Buckley and Harary 1988).

Elke wielgrafiek is een zelfduale grafiek.

Wielgrafieken kunnen in de Wolfram Language worden geconstrueerd met WheelGraph. Vooraf berekende eigenschappen van een aantal wielgrafieken zijn beschikbaar via GraphData.

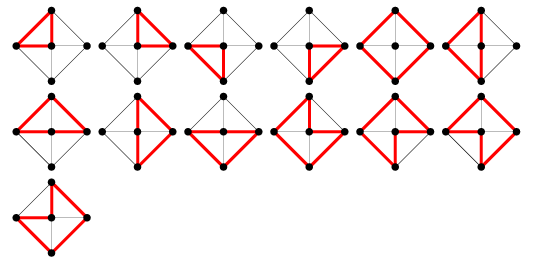
Het aantal grafiekcycli in de wielgrafiek wordt gegeven door , of 7, 13, 21, 31, 43, 57, … (OEIS A002061) voor , 5, ….

In een wielgrafiek heeft het knooppunt graad , en hebben de andere knooppunten graad 3. Wielgrafieken zijn 3-connected. , waarbij de volledige grafiek van orde vier is. Het chromatische getal van is

(1)

De wielgrafiek heeft chromatische polynoom

(2)