Logistische regressie, ook bekend als binaire logit en binaire logistische regressie, is een bijzonder nuttige voorspellende modelleringstechniek. Het wordt gebruikt om uitkomsten te voorspellen waarbij twee opties een rol spelen, bijvoorbeeld of je wel of niet hebt gestemd. Hieronder zal ik proberen alleen uit te leggen wat de gewichten betekenen als je ze gebruikt voor interpretaties.

De interpretatie van de gewichten bij logistische regressie verschilt van de interpretatie van de gewichten bij lineaire regressie, omdat de uitkomst bij logistische regressie een kans tussen 0 en 1 is. De gewichten beïnvloeden de kans dus niet meer lineair. De gewogen som wordt door de logistische functie getransformeerd tot een waarschijnlijkheid. Daarom moeten we de vergelijking voor de interpretatie zo herformuleren dat alleen de lineaire term aan de rechterkant van de formule staat.

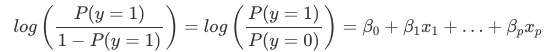
We noemen de term in de log()-functie “odds” (kans op gebeurtenis gedeeld door kans op geen gebeurtenis) en verpakt in de logaritme heet hij log odds.

Uit deze formule blijkt dat het logistische regressiemodel een lineair model is voor de log odds. Geweldig! Dat klinkt niet handig! Met een beetje herschikken van de termen, kunt u uitzoeken hoe de voorspelling verandert als een van de kenmerken xjxj met 1 eenheid wordt veranderd. Om dit te doen kunnen we eerst de exp() functie toepassen op beide zijden van de vergelijking:

Dan vergelijken we wat er gebeurt als we een van de kenmerkwaarden met 1 verhogen. Maar in plaats van te kijken naar het verschil, kijken we naar de verhouding van de twee voorspellingen:

We passen de volgende regel toe:

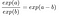
En we verwijderen veel termen:

Op het einde hebben we zoiets simpels als exp() van een feature weight. Een verandering in een kenmerk met één eenheid verandert de odds ratio (vermenigvuldigend) met een factor exp(βj)exp(βj). We kunnen het ook zo interpreteren: Een verandering in xjxj met één eenheid verhoogt de log odds ratio met de waarde van het corresponderende gewicht. De meeste mensen interpreteren de odds ratio omdat het denken over de log() van iets bekend staat als moeilijk voor de hersenen. Het interpreteren van de odds ratio vergt al enige gewenning. Als je bijvoorbeeld odds hebt van 2, betekent dat dat de kans op y=1 twee keer zo groot is als y=0. Als je een gewicht (= log odds ratio) hebt van 0,7, dan vermenigvuldigt het verhogen van het betreffende kenmerk met één eenheid de odds met exp(0,7) (ongeveer 2) en verandert de odds in 4. Maar meestal ga je niet om met de odds en interpreteer je de gewichten alleen als de odds ratio’s. Want om de odds werkelijk te berekenen zou je voor elk kenmerk een waarde moeten instellen, wat alleen zin heeft als je naar één specifieke instantie van je dataset wilt kijken.

Dit zijn de interpretaties voor het logistische regressiemodel met verschillende kenmerktypen:

• Numeriek kenmerk: Als u de waarde van kenmerk xjxj met één eenheid verhoogt, veranderen de geschatte kansen met een factor van exp(βj)exp(βj)
• Binaire categorische kenmerk: Een van de twee waarden van het kenmerk is de referentiecategorie (in sommige talen, de categorie gecodeerd in 0). Verandering van het kenmerk xjxj van de referentiecategorie naar de andere categorie verandert de geschatte kans met een factor exp(βj)exp(βj).
• Categorisch kenmerk met meer dan twee categorieën: Een oplossing om met meerdere categorieën om te gaan is one-hot-encoding, wat betekent dat elke categorie zijn eigen kolom heeft. Je hebt maar L-1 kolommen nodig voor een categorisch kenmerk met L categorieën, anders is het over-parameterized. De L-de categorie is dan de referentiecategorie. Je kunt elke andere codering gebruiken die in lineaire regressie gebruikt kan worden. De interpretatie voor elke categorie is dan gelijk aan de interpretatie van binaire kenmerken.
• Intercept β0β0: Wanneer alle numerieke kenmerken nul zijn en de categorische kenmerken in de referentiecategorie liggen, zijn de geschatte kansen exp(β0)exp(β0). De interpretatie van het interceptgewicht is meestal niet relevant.