GeeksforGeeks
Weighted Sum Method is een multi-criterium besluitvormingsmethode waarbij er meerdere alternatieven zijn en we het beste alternatief moeten bepalen op basis van meerdere criteria. Er zijn andere methoden beschikbaar, waaronder Weighted Product Method (WPM), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), VIKOR, MOORA, GTMA enz. Laten we de werking van de Gewogen Som Methode met een voorbeeld begrijpen.
Neem een geval waarin we de beste kandidaat moeten selecteren uit 5 kandidaten die voor een gesprek verschijnen. Tabel 1 bevat de gegevens van 5 studenten, waaronder hun CGPA, het salaris dat zij per maand verwachten, hun scores op het technische examen en de cijfers die zij op de proeve van bekwaamheid hebben behaald.
Tabel 1: Voorbeeld van een gegevensverzameling
| Attribuut | CGPA | Verwacht salaris | Score technisch examen | Bekwaamheidstest Rang |
|---|---|---|---|---|
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Beschouw de door het interviewpanel aangenomen gewichten als volgt :
CGPA = 30%, Verwacht stipendium = 20%, Technische Examenscore = 25%, Aptitute Test Grade = 25%
Tabel 2: De gewichten van elk attribuut
| Attribuut | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72 | B1 |
| Student 2 | 7.6 | 8500 | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2 |
| Student 5 | 9.3 | 14000 | 72 | A2 |
Belangrijke eigenschap is er een waarbij de persoon maximale waarden wenst. Hier zijn CGPA, de score op het technisch examen en de score op de proeve van bekwaamheid gunstige eigenschappen, omdat het bedrijf verwacht dat de studenten meer van deze eigenschappen bezitten.
Niet-beneficiële eigenschap is er een waarbij minimumwaarden worden gewenst. In dit geval is het verwachte salaris een niet-belunstigende eigenschap. Het bedrijf trekt mensen aan die bereid zijn meer te werken met een laag salaris.
Nu gaan we kijken welke student door het bedrijf wordt geselecteerd met behulp van de methode Gewogen som.
Daartoe moeten we de waarden in tabel 2 normaliseren.
- Voor gunstige eigenschappen,
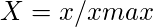
- Voor niet-voordelige eigenschappen,
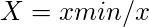
Tabel 3: Bepaling van de maximumwaarde voor een gunstige eigenschap en de minimumwaarde voor een niet-voordelige eigenschap
| Eigenschap | CGPA | Expected Stipendium | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | B1 |
| Student 2 | 7.6 | 8500(min) | 68 | B1 |
| Student 3 | 8.2 | 9500 | 63 | B2 |
| Student 4 | 8.5 | 10000 | 70 | A2(max) |
| Student 5 | 9.3(max) | 14000 | 72 | A2 |
Wij zullen de volgende punten in aanmerking nemen voor het cijfersysteem
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
Tabel 4: Updating the aptitude test grades
| Attribute | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9 | 12000 | 72(max) | 3 |
| Student 2 | 7.6 | 8500(min) | 68 | 3 |
| Student 3 | 8.2 | 9500 | 63 | 2 |
| Student 4 | 8.5 | 10000 | 70 | 4(max) |
| Student 5 | 9.3(max) | 14000 | 72 | 4 |
Normaliseer de waarden voor het respectieve kenmerk, afhankelijk van het voordelige en het niet-voordelige kenmerk.
Tabel 5: Normalisatie
| Attribuut | CGPA | Expected Stipendium | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 9/9.3 | 8500/12000 | 72/72 | 3/4 |
| Student 2 | 7.6/9.3 | 8500/8500 | 68/72 | 3/4 |
| Student 3 | 8.2/9.3 | 8500/9500 | 63/72 | 2/4 |
| Student 4 | 8.5/9.3 | 8500/10000 | 70/72 | 4/4 |
| Student 5 | 9.3/9.3 | 8500/14000 | 72/72 | 4/4 |
Tabel 6: De gewicht-genormaliseerde beslissingsmatrix
| Attribuut | CGPA | Verwacht stipendium | Technische Exam Score | Aptitude Test Rang |
|---|---|---|---|---|
| Gewicht | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.9677 | 0.7083 | 1 | 0.75 |
| Student 2 | 0.8172 | 1 | 0.9444 | 0.75 |
| Student 3 | 0.8817 | 0.8947 | 0.875 | 0.5 |
| Student 4 | 0.9134 | 0.85 | 0.9722 | 1 |
| Student 5 | 1 | 0.6071 | 1 | 1 |
Tabel 7: Vermenigvuldiging van elke parameter met de respectieve gewichten
| Attribuut | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.9677 × 0.3 | 0.7083 × 0.2 | 1 × 0.25 | 0.75 × 0.25 |
| Student 2 | 0.8172 × 0.3 | 1 × 0.2 | 0.9444 × 0.25 | 0.75 × 0.25 |
| Student 3 | 0.8817 × 0.3 | 0.8947 × 0.2 | 0.875 × 0.25 | 0.5 × 0.25 |
| Student 4 | 0.9134 × 0.3 | 0.85 × 0.2 | 0.9722 × 0.25 | 1 × 0.25 |
| Student 5 | 1 × 0.3 | 0.6071 × 0.2 | 1 × 0.25 | 1 × 0.25 |
De bovenstaande tabel is als volgt vereenvoudigd
Tabel 8: Vereenvoudigde versie van tabel 7
| Attribuut | CGPA | Expected Stipend | Technical Exam Score | Aptitude Test Grade |
|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 |
| Student 1 | 0.29031 | 0,14166 | 0,25 | 0,1875 |
| Student 2 | 0,14166 | 0,25 | 0,1875 | |
| .24516 | 0.2 | 0.2361 | 0.1875 | |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 |
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 |
| Student 5 | 0.3 | 0.12142 | 0.25 | 0.25 |
We moeten de componenten in elke rij optellen en de gewogen som berekenen die de prestatiescore is en de prioriteiten aan de leerlingen geven
Tabel 9: Berekening van de rangorde van de studenten naar prestatiescore
| Attribuut | CGPA | Verwacht stipendium | Technical Exam Score | Aptitude Test Grade | Performance Score | Rank | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight | 0.3 | 0.2 | 0.25 | 0.25 | |||||||
| Student 1 | 0.29031 | 0.14166 | 0.25 | 0.1875 | 0.86947 | 3 | |||||
| Student 2 | 0,24516 | 0,2 | 0,2361 | 0,2361 | 0,25 | 0,25 | 0,1875 | 0,25 | .1875 | 0.86876 | 4 |
| Student 3 | 0.26451 | 0.17894 | 0.21875 | 0.125 | 0.7872 | 5 | |||||
| Student 4 | 0.27402 | 0.17 | 0.24305 | 0.25 | 0.93707 | 1 | |||||
| Student 5 | 0.3 | 0.12142 | 0.25 | 0.25 | 0.92142 | 2 |
Conclusie : Uit de Gewogen Som Methode wordt besloten dat Student 4 de beste keuze is onder de anderen.