Loops

“Loop statements” zijn niets anders dan het automatiseren van meerstappen-processen door het organiseren van reeksen acties, en het groeperen van de delen die herhaald moeten worden. Iteratie (of Looping), ook een centraal onderdeel van programmeren, geeft computers veel van hun kracht. Zij kunnen een opeenvolging van stappen zo vaak herhalen als nodig is, en passende herhalingen van eenvoudige stappen kunnen complexe problemen oplossen.

In het algemeen zijn er twee soorten “Looping-technieken”:

1. “For Loops”: zijn die welke een voorgeschreven aantal keren worden uitgevoerd, zoals gecontroleerd door een teller of een index.
2. “While Loops” en “Repeat Loops”: zijn gebaseerd op het begin en de verificatie van een logische voorwaarde. De voorwaarde wordt getest aan het begin of aan het eind van de lusconstructie.

Laten we ze eens bekijken:

1) For Loops

In deze besturingsstructuur worden statements achter elkaar uitgevoerd in een opeenvolgende volgorde over een reeks waarden die alleen wordt geëvalueerd wanneer de “For Loop” wordt gestart (nooit opnieuw geëvalueerd). In dit geval is het aantal iteraties vast en van tevoren bekend.

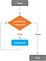
Als de evaluatie van de voorwaarde op een variabele (die waarden binnen een gespecificeerde reeks kan aannemen) WAAR oplevert, worden een of meer verklaringen achtereenvolgens uitgevoerd over die reeks van waarden. Zodra de eerste voorwaardetest is uitgevoerd (en TRUE oplevert), wordt het statement uitgevoerd en wordt de voorwaarde opnieuw geëvalueerd, waarbij een iteratief proces wordt doorlopen. Het onderdeel “variabele in reeks” voert deze test uit op elke waarde van de reeks tot het laatste element is bereikt.

Als niet aan de voorwaarde wordt voldaan en het resultaat FALSE is (d.w.z. als het onderdeel “variabele in reeks” alle elementen van de reeks heeft doorgenomen), eindigt de lus. Als de voorwaardetest in de eerste iteratie FALSE oplevert, wordt de “For Loop” nooit uitgevoerd.

De syntaxis van “For Loops” is:

Voorbeeld 1

Om te laten zien hoe “For Loops” werken, maken we eerst een reeks door verschillende namen van vruchten aan elkaar te plakken om een lijst te maken (genaamd “fruit_list”):

We gebruiken deze fruitlijst als “sequentie” in een “For Loop”, en laten de “For Loop” één keer een instructie uitvoeren (de naam van elke waarde afdrukken) voor elke waarde in de sequentie (de verschillende vruchten in de fruitlijst):

Op deze manier ziet de uitkomst van de “For Loop” er als volgt uit:

## "Apple"
## "Kiwi"
## "Orange"
## "Banana"

OK, we hebben dus de naam van elke waarde in de lijst afgedrukt. Niet zo erg, toch? Het mooie is dat “For Loops” kunnen worden gebruikt om interessantere resultaten te produceren. Kijk eens naar het volgende voorbeeld.

Voorbeeld 2

Wat als we waarden willen wijzigen, of berekeningen achtereenvolgens willen uitvoeren? Je kunt “For Loops” gebruiken om wiskundige bewerkingen sequentieel uit te voeren over elke waarde van een vector (elementen van hetzelfde type, wat in dit geval numeriek zal zijn).

In dit voorbeeld maken we een reeks getallen (van 1 tot 10), en stellen we een “For Loop” in om de vierkantswortel van elke waarde in die reeks te berekenen en af te drukken:

In dit geval is het resultaat van de “For Loop”:

 1
 1.414214
 1.732051
 2
 2.236068
 2.449490
 2.645751
 2.828427
 3
 3.162278

Je kunt elk type wiskundige operator over een numerieke reeks gebruiken, en zoals we later in dit artikel zullen zien, allerlei combinaties maken tussen verschillende Control Structures om complexere resultaten te bereiken.

2) Terwijl-lussen

In “Terwijl-lussen” wordt eerst een voorwaarde geëvalueerd, en als het resultaat van het testen van die voorwaarde WAAR is, worden een of meer statements herhaaldelijk uitgevoerd totdat die voorwaarde ONWAAR wordt.

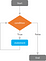
In tegenstelling tot “If-statements”, waarin een als WAAR geteste voorwaarde een expressie slechts eenmaal uitvoert en eindigt, zijn “While Loops” iteratieve statements die een of andere expressie steeds opnieuw uitvoeren totdat de voorwaarde ONWAAR wordt. Als de voorwaarde nooit FALSE wordt, zal de “While Loop” eeuwig doorgaan en zal het programma crashen. Omgekeerd, als de voorwaarde test FALSE wordt in het begin van de lus, zal de uitdrukking nooit uitgevoerd worden.

De syntax van “While Loops” is:

Voorbeeld 1

Laten we eens een voorbeeld bekijken. Eerst maken we een variabele (x) en kennen die de waarde 1 toe. Vervolgens stellen we een “While Loop” in om iteratief een voorwaarde over die variabele te testen totdat de voorwaarde test FALSE oplevert:

Dit is hoe het werkt: de beginwaarde van de variabele (x) is 1, dus wanneer we de voorwaarde testen “is de variabele (x) kleiner dan 10?”, evalueert het resultaat naar TRUE en wordt de expressie uitgevoerd, waarbij het resultaat van de variabele (x) wordt afgedrukt, dat in het eerste geval 1 is. Maar dan gebeurt er iets: de variabele (x) wordt met 1 verhoogd voordat de functie eindigt, en in de volgende iteratie zal de waarde van x 2 zijn.

Deze hertoekenning van de variabele is belangrijk omdat uiteindelijk de conditie FALSE wordt bereikt en de lus wordt beëindigd (waarde van x = 10). Het niet veranderen van de beginvoorwaarden in een “While Loop” zal resulteren in een oneindige lus en een programma crash.

Output

 1
 2
 3
 4
 5
 6
 7
 8
 9

Example 2

Heb je wel eens gehoord van de Fibonacci reeks? Dit is een getallenreeks met de eigenschap dat het volgende getal in de reeks wordt gevonden door de twee getallen ervoor op te tellen: 0, 1, 1, 2, 3, 5, 8, 13, 21,… Deze reeks is terug te vinden in verschillende natuurverschijnselen, en heeft verschillende toepassingen in financiën, muziek, architectuur, en andere disciplines.

Laten we deze berekenen met behulp van een “While Loop”.

In dit geval stellen we een maximumwaarde in de reeks in als stopvoorwaarde, zodat de lus de Fibonacci reeks alleen afdrukt voor getallen onder de 100. Wanneer een serie-element (wat het ook is) groter wordt dan 100, eindigt de lus-cyclus.

 0
 1
 1
 2
 3
 5
 8
 13
 21
 34
 55
 89

Voorbeeld 3

Een andere manier om de Fibonacci serie te genereren met een “While Loop” is, in plaats van de maximum waarde van de serie als stopvoorwaarde in te stellen, het aantal serie-elementen in te stellen dat u wilt genereren.

Deze “While Loop” voegt het volgende element van de reeks toe aan het einde van het vorige element, totdat een stopvoorwaarde wordt bereikt. In dit geval, als de reeks 10 elementen bereikt (ongeacht welke waarden), eindigt de lus cylce.

Output

 0 1 1 2 3 5 8 13 21 34

3) Repeat Loops

Nauw verbonden met “While Loops”, “Repeat Loops” voeren verklaringen iteratief uit, maar totdat aan een stopvoorwaarde is voldaan. Op deze manier worden verklaringen ten minste één keer uitgevoerd, ongeacht wat het resultaat van de voorwaarde is, en wordt de lus alleen afgesloten wanneer een bepaalde voorwaarde WAAR wordt:

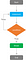
De syntaxis van “Repeat Loops” is:

“Herhaalde lussen” gebruiken “Break statements” als een stopvoorwaarde. “Break statements” worden gecombineerd met de test van een voorwaarde om cycli binnen lussen te onderbreken, aangezien het programma bij een break de besturing doorgeeft aan de instructie onmiddellijk na het einde van de lus (als die er is).

“Repeat Loops” blijven eeuwig doorlopen als niet aan de break-conditie wordt voldaan. Zie deze 2 voorbeelden

Voorbeeld 1

Eerst maken we een variabele (x) en kennen we er de waarde 5 aan toe. Dan stellen we een “Repeat Loop” in om iteratief de waarde van de variabele af te drukken, de waarde van de variabele te wijzigen (verhogen met 1), en een voorwaarde over die variabele te testen (of deze gelijk is aan 10) totdat de voorwaarde test als resultaat TRUE heeft.

De “breekvoorwaarde” treedt in werking wanneer de variabele (x) 10 bereikt, en de lus eindigt.

Uitvoer

 5
 6
 7
 8
 9

Voorbeeld 2

Nemen we nu aan dat we een lijst willekeurige getallen produceren, waarvan we de volgorde of volgorde van genereren niet kennen.

In dit voorbeeld zullen we een “Repeat Loop” gebruiken om een reeks normaal verdeelde willekeurige getallen te genereren (je kunt willekeurige getallen genereren met elke andere verdeling, we kiezen gewoon deze), en de reeks breken zodra een van die getallen groter is dan 1. Omdat we niet weten welke getallen eerst komen, weten we ook niet hoe lang de reeks zal zijn: we weten alleen de breekvoorwaarde.

Eerst gebruiken we de “set.seed” instructie om de willekeurige getallen vast te zetten (altijd dezelfde willekeurige getallen genereren), en dit voorbeeld reproduceerbaar te maken.

Dan starten we de “Repeat Loop” door een normaal verdeeld willekeurig getal te genereren, dat af te drukken, en te controleren of dat getal groter is dan 1. Pas als deze voorwaarde WAAR wordt (kan met het eerste gegenereerde getal zijn, of niet), gaat de luscyclus over naar het break statement en eindigt.

Output

 -0.9619334
 -0.2925257
 0.2587882
 -1.152132
 0.1957828
 0.03012394
 0.08541773
 1.11661

Hieruit blijkt eens te meer hoe belangrijk het is om een goede breekvoorwaarde in te stellen. Als je dat niet doet, krijg je een oneindige lus.

Eindgedachten

We hebben concepten afzonderlijk gezien en uitgelegd, maar “Control Structures” kun je combineren zoals je wilt: Lussen kunnen meerdere interne Lussen bevatten; Conditionals kunnen Lussen en Conditionals bevatten, de mogelijkheden zijn eindeloos. (In feite, bij het bekijken van “Repeat Loops” ontdekten we dat de voorbeelden geneste “If statements” bevatten).

Je kunt geavanceerde oplossingen ontwikkelen door gewoon de “Control Structures” te combineren die we in dit artikel hebben uitgelegd. Zoals Minsky stelde, kunnen we complexe uitkomsten bereiken als resultaat van de interactie van eenvoudiger componenten. Control Structures vormen de basisblokken voor besluitvormingsprocessen in de informatica. Ze veranderen de stroom van programma’s en stellen ons in staat om complexe reeksen instructies te construeren uit eenvoudigere bouwstenen.

Mijn advies is: leer erover.

Het zal je weg vergemakkelijken bij het coderen en begrijpen van programma’s, en het zal je helpen nieuwe manieren te vinden om problemen op te lossen.