Articles

GeeksforGeeks

by admin

Weighted Sum Methodは、複数の代替案があり、複数の基準に基づいて最良の代替案を決定しなければならない多基準意思決定法である。 他にも加重積法（WPM）、理想解類似度優先順位法（TOPSIS）、VIKOR、MOORA、GTMAなどの方法があります。 949>

面接を受ける5人の候補者の中から最も優秀な候補者を選ばなければならない場合を考えてみましょう。 表1は、5人の学生の詳細で、CGPA、月給、技術試験の成績、適性試験の成績が記載されています。

表1: サンプルデータセット

B1

属性 CGPA 希望給与 技術試験スコア 適性試験 成績
生徒1 9 12000 72 B1
生徒2 7.6 8500 68 B1
Student 3 8.2 9500 63 B2
学生 4 8.5 10000 70 A2
学生 5 9・9・9・9 8.5> 8.5> B2 B1 14000 72 A2

面接委員が想定する重みを次のように考える：
CGPA=30%、期待報酬=20%、専門試験スコア=25%、適性試験成績=25%

表2.面接委員が想定する重みは次の通りである。 各属性の重み

＜9147>9.0＜9147>9.0

学生3

属性 CGPA Expected Stipend Technical Exam Score Aptitude Test Grade
重み 0.3 0.2 0.25 0.25
生徒1 12000 72 B1
生徒2 7.0 7.0 9.0 8500 68 B1
Student 3 8.2 9500 63 B2
学生 4 8.5 10000 70 A2
学生 5 97.0 9.0 14000 72 A2

有益属性とは、人が最大値を欲するものである。 ここでは、CGPA、技術試験の点数、適性検査の点数が有益な属性であり、企業はこれらの属性をより多く持っている学生を期待していることになります。 この場合、期待される俸給は非利益的属性である。

ここで、重み付き和算法を用いて、どの学生が会社に選ばれるかを見てみましょう。
このためには、表2の値を正規化する必要があります。

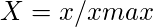
  1. 有益な属性については、 X=x/xmax
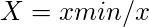
  2. 有益でない属性については、 X=xmin/x

表3． 有益な属性の最大値と有益でない属性の最小値を決める

9

属性 CGPA 期待支給額 技術試験スコア 適性試験成績
重み 0.3 0.2 0.25 0.25
生徒1 12000 72(max) B1
生徒2 7.1 7.6 8500(min) 68 B1
Student 3 8.2 9500 63 B2
Student 4 8.5 10000 70 A2(max)
Student 5 9.3(max) 14000 72 A2

等級制度については以下の点を考慮します
A1 – 5
A2 – 4
B1 – 3
B2 – 2
C1 – 1
表4.1
表4: 適性検査成績の更新

12000

8.2

65 65 65 65生徒3

8.05

属性 CGPA 期待支給額 技術試験スコア 適性検査成績
重み 0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.3 0.2 0.25 0.25
生徒1 9 72(max) 3
生徒2 7.1 7.6 8500(min) 68 3
生徒3 9500 63 2
生徒4 8.0 生徒6 8500(min) 65 65 10000 70 4(max)
Student 5 9.3(max) 14000 72 4

有益属性と非有益属性に応じてそれぞれの属性の値を正規化します。
表5：正規化

9/9.2

属性 CGPA 予想俸給 技術試験スコア 適性試験グレード
重み 0.5%。3 0.2 0.25
生徒1 0.25 0.25 0.2 0.25 0.25 0.253 8500/12000 72/72 3/4
Student 2 7.9.6/9.3 8500/8500 68/72 3/4
Student 3 8.1.2/9.3 8500/9500 63/72 2/4
Student 4 8.8.5/9.3 8500/10000 70/72 4/4
Student 5 9.3/9.3 8.3 8500/14000 72/72 4/4

Table 6: Weight- Normalized decision matrix

0.9677

0.8817

0.875

0.9134

生徒5

Attribute CGPA Expect Stipend Technical Exam Score Aptitude Test Grade
Weight 0.0.3 0.2 0.25
生徒1 0.7083 1 0.25
1.25 0.25> 0.25> 0.25> 0.25> 0.25> 0.25> 0.2575
生徒2 0.8172 1 0.9444 0.75
生徒3 0.8947 0.877> 1 1 0.5
生徒4 0.85 0.9722 1
1 0.5 0.5> 0.6071 1

表7: 各パラメータにそれぞれの重みを掛ける

0.75 × 0.25 0.0

0.9134 × 0.3

属性 CGPA 期待支給額 技術試験スコア 適性試験成績
重み 0.0。3 0.2 0.25
生徒1 0.9677×0.3 0.7083 × 0.2 1 × 0.25 0.75 × 0.25
Student 2 0.75×0.25×0.8172 × 0.3 1 × 0.2 0.9444 × 0.25 0.75 × 0.25
Student 3 0.3 0.8947 × 0.2 0.875 × 0.25 0.5 × 0.25
生徒4 0.85 × 0.2 0.9722 × 0.0.25 1 × 0.25
学生5 1 × 0.3 0.6071 × 0.2 1 × 0.25 0.6071 × 0.225 1 × 0.25

上記の表を簡略化すると
表8.のようになります。 表7の簡略版

。29031

0.14166

0.24516

0.27402

0.3

属性 CGPA 期待支給額 技術試験スコア 適性試験成績
重量 0・0.3 0.2 0.25
生徒1 0.25 0.14166 0.25 0.1875
Student 2 0.1875 0.14166 0.25 1 0.2 0.2361 0.1875
Student 3 0.26451 0.1875 0.17894 0.21875 0.125
生徒4 0.17 0.17 0.24305 0.25
生徒5 0.12142 0.25 0.25 0.25

各行の成分を加算し、パフォーマンススコアである加重合計を計算し、学生に優先順位を与える必要がある
表9: パフォーマンススコアによる学生のランクの計算

生徒2

0.24516

0.26451

。27402

0.3

属性 CGPA 予想支給額 技術試験成績 適性試験成績 成績順位
体重 0.3 0.2 0.25
生徒1 0.29031 0.14166 0.25 0.1875 0.25 0.25> 0.25> 0.25> 0.25> 生徒3 0.25> 生徒4 0.261 3
学生2 0.2 0.2361 0.1 0.2 0.1875 0.86876 4
学生3 0.17894 0.21875 0.125 0.7872 5
Student 4 0.7851 0.7851
0.7851 0.17 0.24305 0.25 0.93707 1
学生5 0.12142 0.0.25 0.25 0.92142 2

結論: Weighted Sum Methodから、生徒4が他の生徒の中で最も良い選択であると判断される。

Article Tags :

練習用タグ :