Loop

“Loop statement” は、一連の動作を整理し、繰り返す必要のある部分をグループ化して、複数ステップの処理を自動化することに他なりません。 また、プログラミングの中心的な部分である反復処理 (またはループ) は、コンピューターに多くの力を与えています。

一般論として、「ループ技術」には2つのタイプがある。

1. 「Forループ」は、カウンタやインデックスによって制御され、所定の回数だけ実行されるものである。

では、これらについて見てみよう。

1) For Loops

この制御構造では、「For Loop」が開始されたときのみ評価される一連の値に対して連続した順序で、ステートメントが次々と実行される（再評価されることはない）。

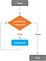
変数の条件評価の結果が TRUE なら、一つまたは複数の文がその値の列の上で順次実行されます。 最初の条件テストが行われると（そして結果が TRUE になると）、ステートメントが実行され、条件が再び評価され、反復プロセスを経る。 variable in sequence」セクションでは、最後の要素をカバーするまで、シーケンスの各値に対してこのテストを実行します。

条件が満たされず、結果の結果が FALSE の場合（たとえば、「 variable in sequence」パートがシーケンスのすべての要素を調べ終えた）、ループは終了します。 最初の反復で条件テストの結果がFALSEの場合、「For Loop」は決して実行されません。

「Forループ」の構文は次のとおり。

例1

Forループがどう動くかを示すために、まず、異なる名前の果物を連結してリスト（「Fruit_list」と呼ぶ）にしたシーケンスを作成します。

このフルーツリストを「シーケンス」として「Forループ」で使用し、シーケンス内の各値（フルーツリストの異なるフルーツ）に対して1回ずつ文を実行（それぞれの値の名前を表示）させることにします。

このようにすると、「Forループ」の結果は次のようになります。 大したことはないでしょう？ 良い点は、「Forループ」を使ってもっと面白い結果を出すことができることです。 次の例を見てください。

例 2

値を変更したり、計算を順次実行したい場合はどうしたらよいでしょうか。 Forループ」を使って、ベクトルの各値（同じ型の要素、この場合は数値）に対して順次数学的演算を実行することができます。

この例では、数字の列（1から10まで）を作成し、その列の各値の平方根を計算して表示する「Forループ」を設定します：

この場合、「Forループ」の結果は、次のようになります。

 1
 1.414214
 1.732051
 2
 2.236068
 2.449490
 2.645751
 2.828427
 3
 3.162278

数値列に対してあらゆるタイプの数学演算子を使用でき、この記事の後半で説明するように、異なる制御構造間のあらゆる種類の組み合わせを行って、より複雑な結果に到達することができます。

2) While Loops

「While Loops」では、最初に条件が評価され、その条件をテストした結果がTRUEなら、その条件がFALSEになるまで1つまたは複数のステートメントが繰り返し実行されます。

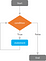
TRUEとテストした条件が一度だけ式を実行して終了する「If文」とは異なり、「While Loop」は、ある式を条件がFALSEになるまで何度でも実行する反復文である。 もし、一度も条件がFALSEにならなかった場合、「While Loop」は永遠に続き、プログラムはクラッシュしてしまう。

「Whileループ」のシンタックスは次のとおりです：

例 1

例を見てみましょう。 まず、変数(x)を作成し、値1を代入します。 次に、「While Loop」を設定して、その変数に対する条件を、条件テストの結果がFALSEになるまで繰り返しテストします：

このように動作します：変数（x）の初期値は1なので、条件テスト「変数（x）は10より小さいか」を行うと、その値は10より小さくなります。”という条件をテストすると、結果は TRUE と評価され、式が実行され、最初のケースでは 1 である変数 (x) の結果が出力されます。しかしその後、何かが起こります。関数が終了する前に変数 (x) が 1 つ増え、次の反復では x の値は 2 になります。

この変数の再配置は、最終的に FALSE 条件とループ終了（x の値 = 10）に到達するため重要なことなのです。

Output

 1
 2
 3
 4
 5
 6
 7
 8
 9

Example 2

Fibonacci sequenceをご存知でしょうか？ これは、0、1、2、3、5、8、13、21、…と、前の2つの数字を足すと次の数字が見つかるという特徴を持つ数列です。この数列は、いくつかの自然現象の中に見つけることができ、金融や音楽、建築など、さまざまな分野で応用することが可能です。

「While Loop」を使って計算してみましょう。

今回は停止条件として系列の最大値を設定し、100以下の数に対してのみフィボナッチ系列を表示させるループを作成しました。

 0
 1
 1
 2
 3
 5
 8
 13
 21
 34
 55
 89

「While Loop」でフィボナッチ級数を生成するもう一つの方法は、停止条件として級数の最大値を設定する代わりに、生成したい級数の要素数を設定することである。

この「While Loop」は停止条件になるまで、系列の次の要素を前の要素の終わりに追加していく。 この場合、シリーズが10要素に達すると（どの値であっても）、ループは終了する。

Output

 0 1 1 2 3 5 8 13 21 34

3) Repeat Loop

While Loopと密接に関連するが、停止条件が満たされるまで繰り返し文を実行するもので、繰り返しループは、停止条件が満たされると繰り返し実行する。 この方法では、条件の結果がどうであれ、文は少なくとも一度は実行され、ある条件が真になったときだけループが終了する。

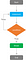
「繰り返しループ」のシンタックスは、次のとおりです。

“Repeat Loop” は停止条件として “Break statement” を使用します。 「ブレークステートメント」は、ループ内のサイクルを中断するための条件テストと組み合わされ、プログラムがブレークにヒットすると、ループの終了直後の命令（もしあれば）に制御が移るからである。 2 つの例を参照してください。

例 1

最初に変数 (x) を作成し、値として 5 を代入します。 次に、「繰り返しループ」を設定して、変数の値を繰り返し表示し、変数の値を変更し (1増加)、その変数に対する条件 (10に等しい場合) を、条件テストの結果が TRUE になるまでテストします。

「破条件」は変数（x）が10に達すると発動し、ループは終了する。

出力

 5
 6
 7
 8
 9

例2

ここで、生成の順序や順番がわからない乱数のリストを生成するとしよう。

この例では、「繰り返しループ」を使用して、正規分布乱数のシーケンスを生成し（他の分布でも生成できるが、ここではこの分布を使用）、これらの数字の1つが1より大きくなったらシーケンスを中断させる。

まず、乱数を固定し（常に同じ乱数を生成）、この例の再現性を高めるために “set.seed” 命令を使用します。

そして、正規分布の乱数を生成してそれを表示し、その数が1より大きいかどうかをチェックすることで「繰り返しループ」を開始します。この条件が真になったときだけ（最初に生成した数でも、そうでなくてもよい）、ループサイクルはブレーク文に移行して終わります。

Final Thoughts

これまでは単体で概念を見て説明してきましたが、「制御構造」は自由に組み合わせることができます。 ループはいくつかの内部ループを含むことができ、条件文はループと条件文を含むことができ、選択肢は無限大です。 (実際、「ループの繰り返し」を見直すと、「If文」が入れ子になっている例がありました。)

今回説明した「制御構造」を組み合わせるだけで高度なソリューションを開発することができるのです。 ミンスキーが述べたように、より単純な構成要素の相互作用の結果として、複雑な結果に到達することができるのです。 制御構造とは、コンピュータにおける意思決定プロセスの基本的なブロックを構成するものです。

私のアドバイスは、制御構造について学ぶことです。

それは、コーディングとプログラムの理解への道を容易にし、問題解決の新しい方法を見つけるのに役立ちます。